Все формулы площади плоских фигур

Все формулы площади плоских фигур

Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

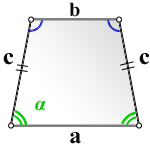
а - нижнее основание

b - верхнее основание

с - равные боковые стороны

α - угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

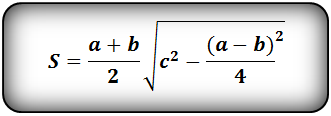
Формула площади равнобедренной трапеции через стороны и угол, (S ):

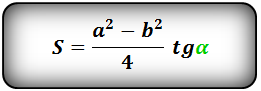
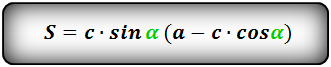
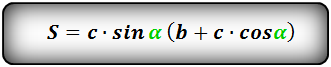
2. Формула площади равнобедренной трапеции через радиус вписанной окружности

R - радиус вписанной окружности

D - диаметр вписанной окружности

O - центр вписанной окружности

H - высота трапеции

α, β - углы трапеции

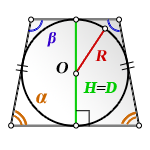
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

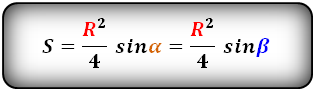
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

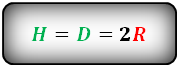
3. Формула площади равнобедренной трапеции через диагонали и угол между ними

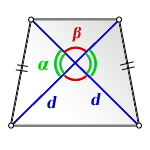
d - диагональ трапеции

α, β - углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

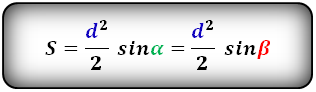
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

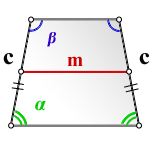
c - боковая сторона

m - средняя линия трапеции

α, β - углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,

(S ):

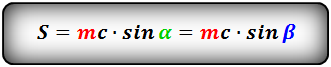
5. Формула площади равнобедренной трапеции через основания и высоту

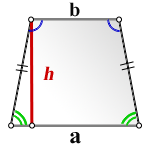
a - нижнее основание

b - верхнее основание

h - высота трапеции

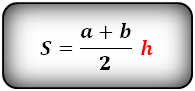
Формула площади равнобедренной трапеции через основания и высоту, (S ):

Площадь треугольника по стороне и двум углам, формула.

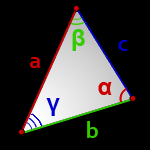
a, b, c- стороны треугольника

α, β, γ- противолежащие углы

Площадь треугольника через сторону и два угла (S):

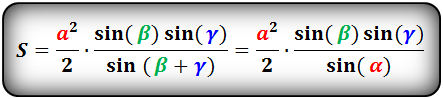
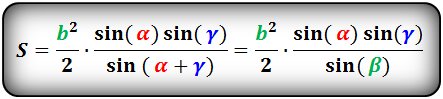
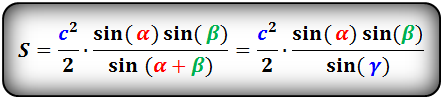
Формула площади правильного многоугольника

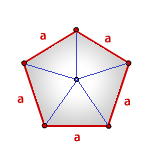
a - сторона многоугольника

n - количество сторон

Площадь правильного многоугольника, (S):

Формула (Герона) площади треугольника через полупериметр (S):

Площадь равностороннего треугольника равна:

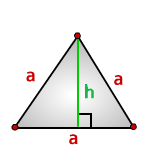
Формулы расчета, площади равностороннего треугольника.

a - сторона треугольника

h – высота

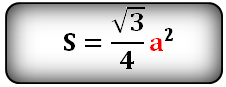
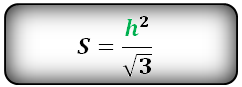
Как вычислить площадь равнобедренного треугольника ?

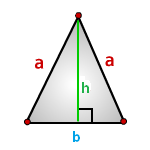
b - основание треугольника

a - равные стороны

h – высота

3. Формула площади трапеции через четыре стороны

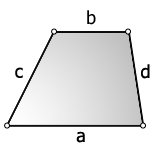
a - нижнее основание

b - верхнее основание

c , d - боковые стороны

Радиус описанной окружности трапеции по сторонам и диагонали

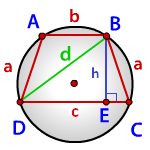
a - боковые стороны трапеции

c - нижнее основание

b - верхнее основание

d - диагональ

h - высота

p = (a+d+c)/2

Формула радиуса описанной окружности трапеции, (R)

найти радиус описанной окружности равнобедренного треугольника по сторонам

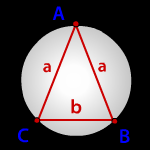
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

a, b - стороны треугольника

Радиус описанной окружности равнобедренного треугольника (R):

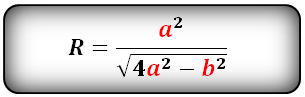
Радиус вписанной окружности в шестиугольник

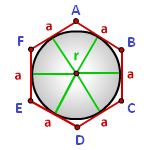
a - сторона шестиугольника

Радиус вписанной окружности в шестиугольник, (r):

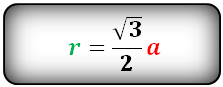
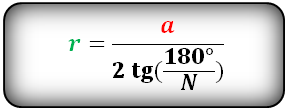
Радиус вписанной окружности в ромб

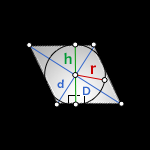
r - радиус вписанной окружности

a - сторона ромба

D, d - диагонали

h - высота ромба

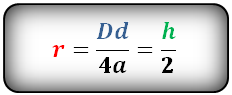
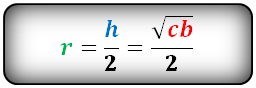
Радиус вписанной окружности в равнобочную трапецию

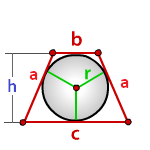
с - нижнее основание

b - верхнее основание

a - боковые стороны

h - высота

Радиус вписанной окружности в прямоугольный треугольник

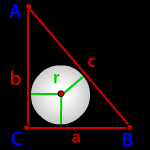
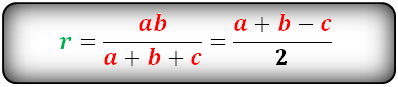
a, b - катеты треугольника

с - гипотенуза

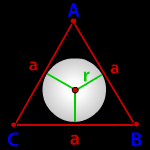
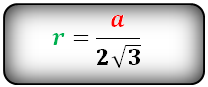
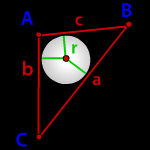
Радиус вписанной окружности в равнобедренный треугольник

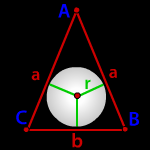
a, b - стороны треугольника

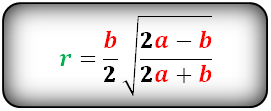
.Доказать, что площадь вписанного четырёхугольника равна

\/(р — а)(р — b) (р — с) (р — d),

где р — полупериметр и а, b, с и d — стороны четырёхугольника.

Доказать, что площадь вписанного в круг четырёхугольника равна

1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.

S = √[ a • ƀ • c • d] • sin ½ (α + β). - Читайте подробнее на FB.ru:

Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:

где р – полупериметр четырёхугольника.

Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты

а описанного (рис. 1.14, б) () – по формуле

Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:

Формула Пика

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, - число клеток, которые целиком лежат внутри многоугольника, и - число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку .

Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:

где - площадь, r – число узлов, которые лежат строго внутри многоугольника.

Эту формулу называют «формула Пика» - по имени математика, открывшего её в 1899 году.

.