теоретическая механика / Задание02

H14.

Механическая система, состоящая из тела 1 массой m = 20кг и цилиндра 2 с моментом инерции относительно оси вращения I=2 кг/м² имеет кинетическую энергию T = 35. Составить уравнение Лагранжа и определить ускорение тела 1, если момент пары сил M = 20 Н/м.

H15.

Кинетическая энергия системы Т = 6, масса тел m₁=m₂=6кг. Составить уравнение Лагранжа и определить ускорение тела 1, если коэффициент трения-скольжения между горизонтальной поверхностью и телом 1 f = 0,2.

H16.

Функция Лагранжа механической системы определена выражением L=14²+2 , где -обобщенная координата. Вычислить обобщенную скорость через 2 секунды после начала движения, если, |_t=0 = 2 рад/сек .

H17.

Функция Лагранжа механической системы L=16x²+20x . Определить значение обобщенной координаты х в момент времени t = 3c, если в начале движения (t=0) x = 0 м/с; x = 2 м/с .

H18.

Кинетическая энергия механической системы Т = 2, потенциальная энергия U = 4x . Определить обобщенную скорость x в момент времени t = 3c, если x|_t=0 = 13 м/с.

H19.

Упругую проволоку, на которой подвешен шар радиуса R и массы m закрутили на малый угол и отпустили. Считая коэффициент упругости кручения проволоки С, составить уравнение Лагранжа системы и определить частоту крутильных колебаний шара.

H20.

Точка массы m движется по поверхности прямого конуса с углом при вершине 2, поставленного вертикально на вершину. Потенциальная энергия точки обратно пропорциональна ее расстоянию от вершины. Составить уравнения Лагранжа.

H 21.

Груз 1 массой m движется по призме 2, которая скользит по горизонтальной плоскости. Кинетическая энергия системы Т = m(+(1/2) +(1/2)) выражена через обобщенные скорости и . Найти ускорения тел 1 и 2.

H22.

Диск массой m, радиуса r скатывается по наклонной плоскости с углом наклона . Составить функцию Лагранжа, уравнение Лагранжа и определить ускорение центра диска.

H23.

Тело массой m соскальзывает по наклонной плоскости с углом наклона . Коэффициент трения k. Написать функцию и уравнение Лагранжа и определить ускорение тела.

H24.

Тело массы m падает в среде с силой сопротивления пропорциональной скорости. Написать функцию и уравнение Лагранжа и определить зависимость от времени скорости тела.

H25.

Шарик подвешен на пружине с коэффициентом упругости k и колеблется в среде с силой сопротивления пропорциональной скорости. Написать функцию и уравнение Лагранжа, определить ускорение.

GH01.

Колесо веса P и радиуса r катится по горизонтальной плоскости без проскальзывания под действием горизонтальной силы , приложенной к центру C этого колеса. Выбирая в качестве обобщенной координаты угол поворота  колеса, определить обобщенную силу Q_, если коэффициент трения качения равен f _k.

Ответ: Q_ = F r - P f _k.

G

H02. Физический маятник состоит из однородного прямолинейного стержня OA длины l и закрепленного на его свободном конце точечного груза А. Пренебрегая сопротивлениями, определить обобщенную силу Q_, соответствующую углу  отклонения маятника от положения его устойчивого равновесия, если веса стержня и груза одинаковы и равны P.

Ответ: Q_ = sin .

GH03.

Двухмассовая механическая система, cостоящая из грузов 1 и 2 и двух невесомых пружин жесткости с₁ и с₂, движется по гладкой горизонтальной плоскости при действии горизонтальной силы , которая приложена к грузу 2. Выбирая в качестве обобщенных координат системы отклонения x₁ и x₂ грузов от положения их статического равновесия, определить обобщенную силу Q₂, соответствующую координате x₂.

Ответ: Q₂ = F - c₂ (x₂ - x₁).

GH04. В механической системе с одной степенью свободы в качестве обобщенной координаты может быть выбрано отклонение одного из грузов m₁ или m₂ от его начального положения. Найти соотношение обобщенных сил Q₁ и Q₂, соответствующих выбираемым таким образом обобщенным координатам. Массами блоков и нитей, а также сопротивлениями пренебречь.

Ответ: Q₁/Q₂ = 1/2.

GH05. Однородный сплошной диск массы М может перекатываться без скольжения по горизонтальной плоскости. К центру О₁ диска прикреплены две одинаковые горизонтальные пружины жесткости с каждая. Пренебрегая массой пружин, определить кинетический потенциал L (функцию Лагранжа) такой механической системы, если в качестве обобщенной координаты выбрана координата x центра колеса, отсчитываемая от положения статического равновесия.

Ответ: L =

GH06. К переброшенной через неподвижный блок нити подвешен подпружиненный снизу груз В. Радиус блока равен r, а жесткость пружины — с. Принимая за обобщенную координату угол поворота  блока, определить соответствующий этой координате коэффициент жесткости c_ системы. Потенциальную энергию системы в положении ее равновесия считать равной нулю.

Ответ: c_=cr².

GH07.

Система состоит из горизонтального бруса АВ массы m и двух одинаковых катков массы m каждый; при этом брус связан с неподвижными стенками двумя пружинами одинаковой жесткости c. Пренебрегая массой пружин и скольжением между брусом и катками, а также между катками и горизонтальной опорной плоскостью, определить коэффициент жесткости системы, соответствующий обобщенной координате x, отсчитываемой от положения равновесия бруса. Катки рассматривать как однородные сплошные диски.

Ответ: c_x = 8c.

GH08.

Механическая система состоит из двух одинаковых блоков, подвижного и неподвижного, массы m каждый, невесомой нерастяжимой нити, переброшенной через эти блоки, и горизонтальной пружины жесткости с. Считая массу каждого из блоков равномерно распределенной по ободу и пренебрегая массой пружины, определить коэффициент жесткости системы, соответствующий обобщенной координате x, равной расстоянию центра подвижного блока в текущий момент времени от его положения при равновесии системы.

Ответ: c_x = 4c.

GH09. Однородный прямолинейный стержень ОА длины l и массы М закреплен в вертикальной плоскости с помощью шарнира O и вертикальной невесомой пружины жесткости с. В положении равновесия стержень горизонтален. Принимая за обобщенную координату угол поворота  и рассматривая малые отклонения стержня от положения его равновесия, определить коэффициенты инерции и жесткости этой системы.

Ответ: а_=; c_=cl².

GH10. 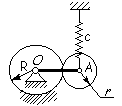Оси двух зубчатых колес радиусов R и r соответственно связаны невесомым стержнем ОА, при этом колесо радиуса R неподвижно, а масса подвижного колеса радиуса r равна m. К концу А стержня ОА прикреплена вертикальная пружина жесткости с. В положении равновесия стержень горизонтален. Найти коэффициенты инерции и жесткости системы, приняв за обобщенную координату угол поворота  стержня при малых его отклонениях от положения равновесия. Подвижное колесо считать однородным сплошным диском.

Ответ: а_ =; c_ =c (R +r)².

GH11. Однородный стержень ОАВ, изогнутый под прямым углом, шарнирно закреплен в точке O и находится в вертикальной плоскости. Найти значение обобщенной координаты  стержня в положении его устойчивого равновесия, если ОА=АВ.

Ответ:  =arctg+.

GH12. К верхнему концу A шарнирно закрепленного однородного стержня ОА веса P и длины l прикреплена пружина, которая при вертикальном положении стержня горизонтальна и не деформирована. Какому условию должна удовлетворять жесткость c пружины, чтобы вертикальное положение стержня было устойчивым?

Ответ: c.

GH13. Груз A закреплен на свободном конце невесомого стержня OA, удерживающегося в вертикальной плоскости с помощью шарнира O и пружины BD. В положении равновесия стержень горизонтален. Как изменится круговая частота k малых колебаний груза, если расстояние OB от шарнира O до точки B крепления пружины к стержню уменьшится в два раза?

Ответ: Уменьшится в 2 раза.

GH14. Однородный сплошной диск массы M закреплен в вертикальной плоскости с помощью шарнира O и пружины жесткости c. В положении равновесия диаметр OA диска вертикален, а пружина горизонтальна и не деформирована. Определить период τ малых колебаний диска около положения его равновесия.

Ответ:.

GH15. Невесомый стержень OA закреплен с помощью шарнира O и двух одинаковых пружин жесткости c каждая. В точках A и D стержня размещены два одинаковых груза, масса каждого из которых равна m. Определить круговую частоту k малых колебаний системы, если в положении равновесия стержень OA горизонтален и OB=BD=DE=EA.

Ответ: .

GH16. В механической системе вертикальная рейка AB закреплена с помощью двух одинаковых пружин жесткости c каждая. Массы рейки и каждого из двух одинаковых зубчатых колес равны m. Пренебрегая массами пружин и считая колеса однородными сплошными дисками, определить круговую частоту k собственных колебаний системы.

Ответ: .