
теоретическая механика / Задание01
.DOC
А 01.
Из пункта А,
находящегося на шоссе (рис.)
необходимо за кратчайшее время попасть
на машине в пункт В,
расположенный в поле на расстоянии
01.
Из пункта А,
находящегося на шоссе (рис.)
необходимо за кратчайшее время попасть
на машине в пункт В,
расположенный в поле на расстоянии
![]() от шоссе. Известно, что скорость машины
по полю в
раз меньше ее скорости по шоссе. На каком
расстоянии от точки D
следует свернуть с шоссе?
от шоссе. Известно, что скорость машины
по полю в
раз меньше ее скорости по шоссе. На каком
расстоянии от точки D
следует свернуть с шоссе?
Ответ:
![]() .
.
А02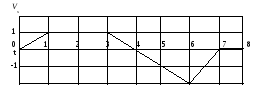 .
Точка движется вдоль оси Х
со скоростью, проекция которой
.
Точка движется вдоль оси Х
со скоростью, проекция которой
![]() ,
как функция времени описывается графиком
на рис. Имея в виду, что в момент t=0
координата точки х=0,
начертить примерные графики зависимости
от времени ускорения аx,
координаты х
и пройденного пути S.
,
как функция времени описывается графиком
на рис. Имея в виду, что в момент t=0
координата точки х=0,
начертить примерные графики зависимости
от времени ускорения аx,
координаты х
и пройденного пути S.
А03. За промежуток времени =10,0 с точка прошла половину окружности радиуса R=160 см, Вычислить за это время:
а) среднее значение модуля скорости v;
б) модуль среднего вектора скорости v;
в) модуль среднего вектора полного ускорения a, если точка двигалась с постоянным тангенциальным ускорением.
Ответ: а) v = R/ = 50 см/с; б) v = 2R/ = 32 см/с; в) a = 2R/2 = 10 см/с2.
А04. Радиус-вектор частицы меняется со временем t по закону r = bt(1-t), где b — постоянный вектор, — положительная постоянная. Найти:
а) скорость v и ускорение а частицы в зависимости от времени;
б) промежуток времени t, по истечении которого частица вернется в исходную точку, а также путь s, который она пройдет при этом.
Ответ: а) v = b(1 – 2t), a = - 2b = const; б) t = 1/; s = b/2.
А05.
В момент t
= 0
частица вышла из начала координат в
положительном направлении оси х.
Ее скорость меняется со временем по
закону
![]() ,
где v0-
начальная скорость, модуль которой v0
=
10
см/с,
= 5,0
с. Найти:
,
где v0-
начальная скорость, модуль которой v0
=
10
см/с,
= 5,0
с. Найти:
а) координату х частицы в моменты времени 6, 10 и 20 с;
б) моменты времени, когда частица будет находиться на расстоянии 10,0 см от начала координат.
Ответ: а) x = v0t(1 – t/2); 0,24; 0 и – 4,0 м; б) 1,1; 9 и 11 с.
А06.
Точка движется, замедляясь, по прямой
с ускорением, модуль которого зависит
от ее скорости
по закону
![]() ,
где
- положительная постоянная. В начальный
момент скорость точки равна 0.
Какой путь она пройдет до остановки? За
какое время этот путь будет пройден?
,
где
- положительная постоянная. В начальный
момент скорость точки равна 0.
Какой путь она пройдет до остановки? За
какое время этот путь будет пройден?
Ответ:
![]() ;
;
![]() .
.
А07. Радиус-вектор точки А относительно начала координат меняется со временем t по закону r = ti + t2j, где и - постоянные, i и j – орты осей x и y. Найти:
а) уравнение траектории точки y(x); изобразить ее график;
б) зависимость от времени скорости , ускорения а и модулей этих величин;
в) зависимость от времени угла между векторами а и .
Ответ:
а)
![]() ;
б)
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
в)
;
в)
![]() .
.
А08.
Тело движется в плоскости xy
по закону
![]() ,
,
![]() ,
где
и -
положительные постоянные. Найти:
,
где
и -
положительные постоянные. Найти:
а)
уравнение траектории точки
![]() ;
;
б) скорость , ускорение а точки в зависимости от времени t;
в)
момент
![]() ,
когда угол между скоростью и ускорением
равен
,
когда угол между скоростью и ускорением
равен
![]() .
.
Ответ:
а)
![]() ;
б)
;
б)
![]() ;
;![]() ;
в)
;
в)
![]() .
.
А09. Точка движется в плоскости xy по закону x = Аsint, y = A(1-cost), где А и - положительные постоянные. Найти:
а) путь s, проходимый точкой за время ;
б) угол между скоростью и ускорением точки.
Ответ: a) s = A; б) /2.
А10.
Частица движется в плоскости XY
с постоянным ускорением а,
направление которого противоположно
положительному направлению оси Y.
Уравнение траектории частицы
имеет вид
![]() ,
где
и
- положительные
постояниые.
Найти скорость частицы в начале координат.
,
где
и
- положительные
постояниые.
Найти скорость частицы в начале координат.
Ответ:
![]() .
.
А11. Небольшое тело бросили под углом к горизонту с начальной скоростью v0. Пренебрегая сопротивлением воздуха, найти:
а) перемещение тела в функции времени r(t);
б) средний вектор скорости < v > за первые t секунд и за все время движения.
Ответ: а) r = v 0t + gt2/2; б) < v >t = v 0 + gt/2; < v > = v 0 – g(v 0g)/g2;
А12.
Тело бросили с поверхности Земли под
углом
к горизонту с начальной скоростью
![]() .
Пренебрегая сопротивлением воздуха,
найти:
.
Пренебрегая сопротивлением воздуха,
найти:
а) время движения;
б) максимальную высоту подъема и горизонтальную дальность полета; при каком значении угла они будут равны друг другу;
в)
уравнение траектории
![]() ,
где у
и х
- перемещение тела по вертикали и
горизонтали соответственно.
,
где у
и х
- перемещение тела по вертикали и
горизонтали соответственно.
Ответ: а) = 2(0/g) sin; б) h = (02/2g) sin2 , l = (02/g) sin2 , = 76o; в) y = x tg - (g/202 cos2) x2.
А13. Шарик падает с нулевой начальной скоростью на гладкую наклонную плоскость, составляющую угол с горизонтом. Пролетев расстояние h, он упруго отразился от плоскости. На каком расстоянии от места падения шарик отразится второй раз?
Ответ: l = 8h sin.
А14. Пушка и цель находятся на одном уровне на расстоянии 5,1 км друг от друга. Через сколько времени снаряд с начальной скоростью 240 м/с достигнет цели?
Ответ: Через 0,41 или 0,71 мин в зависимости от начального угла.
А15.
Частица движется в плоскости ху
со скоростью
![]() ,
где i
и j
— орты осей х
и
у,
и
— постоянные. В начальный момент частица
находилась в точке х
= y
= 0.
Найти:
,
где i
и j
— орты осей х
и
у,
и
— постоянные. В начальный момент частица
находилась в точке х
= y
= 0.
Найти:
а) уравнение траектории частицы у(х);
б) радиус кривизны траектории в зависимости от x.
Ответ:
а)
![]() ;
б)
;
б)
![]() .
.
А16.
Частица движется по дуге окружности
радиуса R
по закону
![]() ,
где
,
где
![]() - смещение из начального положения,
отсчитываемое вдоль дуги, А
и
— постоянные. Положив R
= 1,00
м, A
= 0,8
м и
= 2,00
с -1,
найти полное ускорение частицы в точках
- смещение из начального положения,
отсчитываемое вдоль дуги, А
и
— постоянные. Положив R
= 1,00
м, A
= 0,8
м и
= 2,00
с -1,
найти полное ускорение частицы в точках
![]() = 0 и ±А.
= 0 и ±А.
Ответ:
![]() м/с2;
м/с2;
![]() м/с2.
м/с2.
А17.
Колесо вращается вокруг неподвижной
оси так, что угол
его поворота зависит от времени как
![]() ,
где
= 0,20 рад/с2.
Найти полное ускорение а
точки А
на ободе колеса в момент t
= 2,5 с, если
скорость точки А
в этот момент v
= 0,65 м/с.
,
где
= 0,20 рад/с2.
Найти полное ускорение а
точки А
на ободе колеса в момент t
= 2,5 с, если
скорость точки А
в этот момент v
= 0,65 м/с.
Ответ:
![]() м/с2.
м/с2.
А18.
Твердое тело вращается вокруг неподвижной
оси по закону
![]() ,
где а
= 6,0
рад/с, b
= 2,0
рад/с3.
Найти:
,
где а
= 6,0
рад/с, b
= 2,0
рад/с3.
Найти:
а) средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки;
б) угловое ускорение в момент остановки тела.
Ответ:
а)
= 2а/3
= 4 рад/с;
=
![]() = 6 рад/с2;
б)
= 2
= 6 рад/с2;
б)
= 2![]() = 12 рад/с2.
= 12 рад/с2.
А1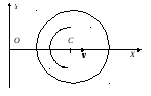 9.
Вращающийся
диск (рис.)
движется в положительном направлении
оси х.
Найти уравнение у(х),
характеризующее положения мгновенной
оси вращения, если в начальный момент
ось С
диска находилась в точке О
и в дальнейшем движется:
9.
Вращающийся
диск (рис.)
движется в положительном направлении
оси х.
Найти уравнение у(х),
характеризующее положения мгновенной
оси вращения, если в начальный момент
ось С
диска находилась в точке О
и в дальнейшем движется:
а)
с постоянной скоростью v,
а диск раскручивается без начальной
угловой скорости с постоянным угловым
ускорением
![]() ;
;
б)
с постоянным ускорением а
(без начальной скорости), а диск вращается
с постоянной угловой скоростью
![]() .
.
Ответ:
а)
![]() (гипербола);
б)
(гипербола);
б)
![]() (парабола).
(парабола).
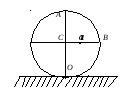
А20. Шар (рис.) радиуса R = 10,0 см катится без скольжения по горизонтальной плоскости так, что его центр движется с постоянным ускорением а = 2,5 см/с2. Через t = 2,0 с после начала движения его положение соответствует рис. Найти:
a) скорости точек А и В;
б) ускорения точек А и О.
Ответ:
![]() =
10 см/с;
=
10 см/с;
![]() =
7 см/с;
=
7 см/с;
![]() см/с2;
аО
=
см/с2;
аО
=
![]() = 2,5 см/с2.
= 2,5 см/с2.
А21. В установке показанной на рис.,
массы тел равны m0,
m1
и m2,
массы блока и нитей пренебрежимо малы
и трения в блоке нет. Найти ускорение
а,
с которым опускается тело m0,
и силу натяжения нити, связывающей тела
m1
и m2,
если коэффициент трения между этими
телами и горизонтальной поверхностью
равен k.
В установке показанной на рис.,
массы тел равны m0,
m1
и m2,
массы блока и нитей пренебрежимо малы
и трения в блоке нет. Найти ускорение
а,
с которым опускается тело m0,
и силу натяжения нити, связывающей тела
m1
и m2,
если коэффициент трения между этими
телами и горизонтальной поверхностью
равен k.
Ответ:
![]() ,
,
![]() .
.![]()
А2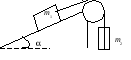 2.
В установке (рис.)
известны угол
и коэффициент трения k
между телом m1
и наклонной плоскостью. Массы блока и
нити пренебрежимо малы, трения в блоке
нет. Вначале оба тела неподвижны. Найти
отношение масс m2/m1,
при котором тело m2
начнет:
2.
В установке (рис.)
известны угол
и коэффициент трения k
между телом m1
и наклонной плоскостью. Массы блока и
нити пренебрежимо малы, трения в блоке
нет. Вначале оба тела неподвижны. Найти
отношение масс m2/m1,
при котором тело m2
начнет:
а) опускаться;
б) подниматься.
Ответ:
а)
![]() ;
б)
;
б)
![]() .
.
А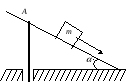 23.
Небольшое тело m начинает скользить по
наклонной плоскости из точки, расположенной
над вертикальным упором
А (рис.).
Коэффициент трения между телом и
наклонной
плоскостью k
= 0,140. При
каком значении угла
время соскальзывания будет наименьшим?
23.
Небольшое тело m начинает скользить по
наклонной плоскости из точки, расположенной
над вертикальным упором
А (рис.).
Коэффициент трения между телом и
наклонной
плоскостью k
= 0,140. При
каком значении угла
время соскальзывания будет наименьшим?
Ответ: tg(2) = -1/k; = 49o.
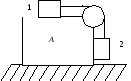
А24. С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок А, чтобы тела 1 и 2 не двигались относительно него? Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен k. Массы блока и нити пренебрежимо малы, трения в блоке нет (рис.).
О
![]() .
.

А25.
Призме 1,
на которой находится брусок 2
массы m,
сообщили влево горизонтальное ускорение
а
(рис.).
При каком максимальном значении этого
ускорения брусок будет оставаться еще
неподвижным относительно призмы, если
коэффициент трения между ними
![]() ?
?
Ответ:
![]() .
.
А26. На горизонтальной поверхности находится призма 1 массы m1 с углом (рис. к задаче А25) и на ней брусок 2 массы m2. Пренебрегая трением, найти ускорение призмы.
Ответ:
![]() .
.
А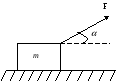 27.
На тело
массы m, лежащее на гладкой горизонтальной
плоскости (рис.),
в момент t
= 0
начала действовать сила, зависящая от
времени как F
= kt, где k
— постоянная.
Направление этой силы все время составляет
угол
с горизонтом. Найти:
27.
На тело
массы m, лежащее на гладкой горизонтальной
плоскости (рис.),
в момент t
= 0
начала действовать сила, зависящая от
времени как F
= kt, где k
— постоянная.
Направление этой силы все время составляет
угол
с горизонтом. Найти:
а) скорость тела в момент отрыва от плоскости;
б) путь, пройденный телом к этому моменту.
Ответ:
a)
![]() ,
,
б)
![]() .
.
А28.
К бруску массы m,
лежащему на гладкой горизонтальной
плоскости, приложили постоянную по
модулю силу
![]() .
В процессе его прямолинейного движения
угол
между направлением этой силы и горизонтом
меняют по закону
.
В процессе его прямолинейного движения
угол
между направлением этой силы и горизонтом
меняют по закону
![]() ,
где k
- постоянная,
S
- пройденный бруском путь (из начального
положения). Найти скорость бруска как
функцию угла .
,
где k
- постоянная,
S
- пройденный бруском путь (из начального
положения). Найти скорость бруска как
функцию угла .
Ответ:
![]() .
.
А29. Тело массы m бросили под углом к горизонту с начальной скоростью 0. Пренебрегая сопротивлением воздуха, найти:
а) приращение импульса тела за первые t секунд движения;
б) модуль приращения импульса тела за все время движения.
Ответ: a) p = mgt; б) |p| = - 2m (0g)/g.
А30.
На покоившуюся частицу массы m
в момент t
= 0
начала действовать сила, зависящая от
времени по закону
![]() ,
где b
- постоянный вектор,
- время, в течение которого действует
данная сила.
Найти:
,
где b
- постоянный вектор,
- время, в течение которого действует
данная сила.
Найти:
а) импульс частицы после окончания действия силы;
б) путь, пройденный частицей, за время действия силы.
Ответ: а) p = b3/6; б) s = b4/12m.
А31.
В момент t
= 0
частица массы m начинает двигаться под
действием силы
![]() ,
где F0
и
- постоянные.
Сколько времени частица будет двигаться
до первой остановки? Какой путь она
пройдет за это время? Какова максимальная
скорость частицы
на этом пути?
,
где F0
и
- постоянные.
Сколько времени частица будет двигаться
до первой остановки? Какой путь она
пройдет за это время? Какова максимальная
скорость частицы
на этом пути?
Ответ: t = /; s = 2F0/m2; макс = F0/m.
А32.
Катер массы m
движется по озеру со скоростью
![]() .
В момент t
= 0
выключили его двигатель. Считая силу
сопротивления пропорциональной скорости
катера,
.
В момент t
= 0
выключили его двигатель. Считая силу
сопротивления пропорциональной скорости
катера,
![]() ,
найти:
,
найти:
а) время движения катера с выключенным двигателем;
б) скорость катера в зависимости от пути, пройденного с выключенным двигателем, а также полный путь до остановки.
Ответ:
а)
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() .
.
А33. Пуля, пробив доску толщиной h, изменила свою скорость от 0 до . Найти время движения пули в доске, считая силу сопротивления пропорциональной квадрату скорости.
Ответ:
![]()
А34. Самолет делает “мертвую петлю” радиуса R = 500 м с постоянной скоростью = 360 км/ч. Найти вес летчика массы m = 70 кг в нижней, верхней и средней точках петли.
Ответ: 2,1; 0,7 и 1,5 кН.
А35. Небольшой шарик массы m, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, и затем отпустили. Найти:
а) модуль полного ускорения шарика и силу натяжения нити в зависимости от — угла отклонения нити от вертикали;
б) силу натяжения в момент, когда вертикальная составляющая скорости шарика максимальна;
в) угол между нитью и вертикалью в момент, когда вектор полного ускорения шарика направлен горизонтально.
Ответ:
а)
![]() ,
,
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
А36. Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения в крайнем и нижнем положениях равны по модулю друг другу. Найти угол отклонения нити в крайнем положении.
Ответ:
![]() ,
,
![]() .
.
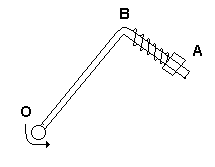
А37. Прибор (рис., вид сверху) состоит из гладкого Г образного стержня, расположенного в горизонтальной плоскости, и муфточки А массы m, соединенной невесомой пружинкой с точкой В, Жесткость пружинки равна . Вся система вращается с постоянной угловой скоростью вокруг вертикальной оси, проходящей через точку О. Найти относительное удлинение пружинки. Как зависит результат от направления вращения? Обосновать ответ.
Ответ: = 1/(/m2 - 1).
А38.
Велосипедист едет по круглой горизонтальной
площадке радиуса R.
Коэффициент трения зависит только от
расстояния r
до центра О
площадки как
![]() ,
где
,
где
![]() — постоянная. Найти радиус окружности
с центром в точке О,
по которой велосипедист может ехать с
максимальной скоростью. Какова эта
скорость?
— постоянная. Найти радиус окружности
с центром в точке О,
по которой велосипедист может ехать с
максимальной скоростью. Какова эта
скорость?
Ответ:
![]() ;
;
![]() .
.
А39.
Автомашина движется равномерно по
горизонтальному пути, имеющему форму
синусоиды
![]() ,
где b
и а
— некоторые постоянные. Коэффициент
трения между колесами и дорогой равен
k.
При какой скорости движение автомашины
будет происходить без скольжения?
,
где b
и а
— некоторые постоянные. Коэффициент
трения между колесами и дорогой равен
k.
При какой скорости движение автомашины
будет происходить без скольжения?
Ответ:
![]() .
.
А40.
Частица движется в положительном
направлении оси x
так, что ее скорость меняется по закону
![]() ,
где
- положительная постоянная. Имея в виду,
что в момент t=0
она находилась в точке x=0,
найти:
,
где
- положительная постоянная. Имея в виду,
что в момент t=0
она находилась в точке x=0,
найти:
а) зависимость от времени скорости и ускорения частицы;
б) среднюю скорость частицы за время, в течение которого она пройдет первые s метров пути.
Ответ:
![]()
А41.
Частица массы m
в момент t=0
начинает двигаться под действием силы
![]() где
F0
и
- постоянные. Найти путь, пройденный
частицей, в зависимости от t.
Изобразить примерный график этой
зависимости.
где
F0
и
- постоянные. Найти путь, пройденный
частицей, в зависимости от t.
Изобразить примерный график этой
зависимости.
Ответ:
![]()
B01. Брусок массой m2 = 5 кг может свободно скользить по горизонтальной поверхности без трения. На нем находится другой брусок массой m1 = 1 кг. Коэффициент трения соприкасающихся поверхностей брусков f = 0,3. Определить максимальное значение силы Fmax, приложенной к нижнему бруску, при которой начнется соскальзывание верхнего бруска.
Ответ: Fmax f (m1 + m2) g = 17,7 Н.
B02. Самолет летит в горизонтальном направлении с ускорением а = 20 м/с2. Какова перегрузка пассажира, находящегося в самолете? (Перегрузкой называется отношение силы F, действующей на пассжира, к его весу mg.)
Ответ: 2,27.
B03. Два конькобежца массами m1 = 80 кг и m2 = 50 кг, держась за концы длинного натянутого шнура, неподвижно стоят на льду один против другого. Один из них начинает укорачивать шнур, выбирая его со скоростью = 1 м/с. С какими скоростями u1 и u2 будут двигаться по льду конькобежцы? Трением пренебречь.
Ответ: u1 = 0,385 м/с; u2 = - 0,615 м/с.
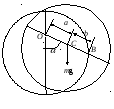
B04. Однородный диск радиусом R = 10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем (рис.). Диск отклонили на угол и отпустили. Определить для начального момента времени угловое и тангенциальное a ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев: 1) a = R, b = R/2, = /2; 2) a = R/2, b = R, = /6; 3) a = 2R/3, b = 2R/3, = 2/3;
Ответ:
=
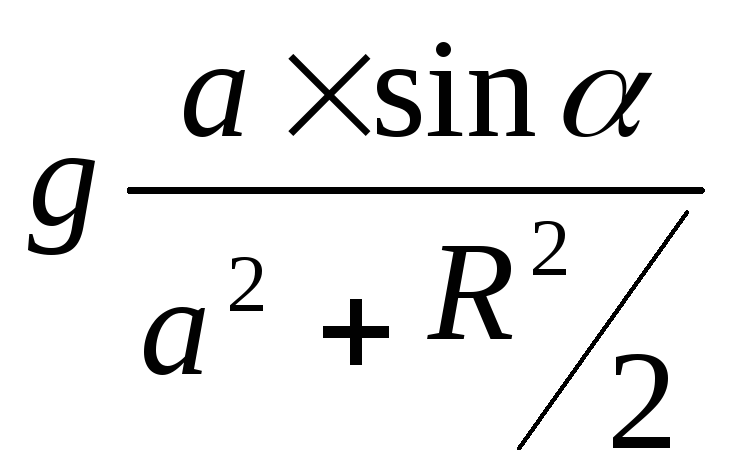 ;
w
=
;
w
=
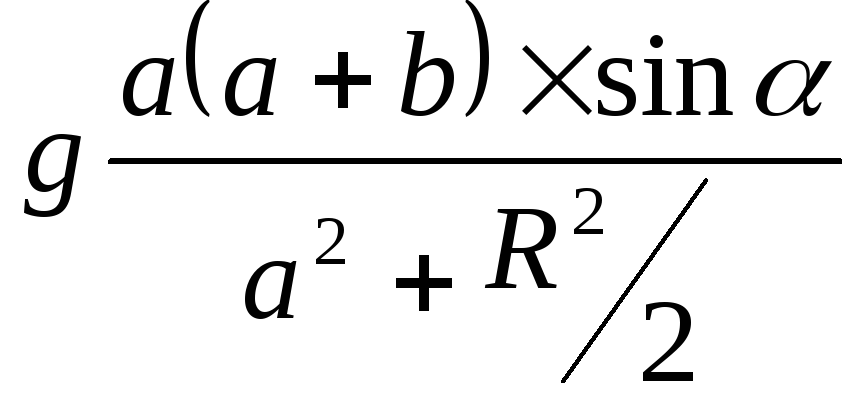 .
1) 65,3 рад/с2,
9,8 м/с2;
2) 32,7 рад/с2,
4,9 м/с2;
3) 59,9 рад/с2,
7,99 м/с2.
.
1) 65,3 рад/с2,
9,8 м/с2;
2) 32,7 рад/с2,
4,9 м/с2;
3) 59,9 рад/с2,
7,99 м/с2.
B05. Тонкий однородный стержень длиной l = 50 см и массой m = 400 г вращается с угловым ускорением = 3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М.
Ответ: М = (1/12)ml2 = 0,025 Нм.
B06. На горизонтальную ось насажены маховик и легкий шкив радиусом R = 5 см. На шкив намотан шнур, к которому привязан груз массой m = 0,4 кг. Опускаясь равноускоренно, груз прошел путь s = 1,8 м за время t = 3 с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой.
Ответ:
![]() 0,0235
кгм2.
0,0235
кгм2.
B07. Вал массой m = 100 кг и радиусом R = 5 см вращался с частотой n = 8 с-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F = 40 Н, под действием которой вал остановился через t = 10 с. Определить коэффициент трения f.
Ответ: f = mRn/(Ft) = 0,31.
B08. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.
Ответ: 1) а1 = 2g/3; 2) a2 = g/2.
B09. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязаны грузики массой m1 = 100 г и m2 = 110 г. С каким ускорением а будут двигаться грузики, если масса m блока равна 400 г? Трение при вращении блока ничтожно мало.
Ответ:
![]() 0,24
м/с2.
0,24
м/с2.
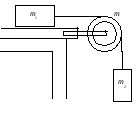
B10. Два тела массами m1 = 0,25 кг и m2 = 0,15 кг связаны тонкой нитью, переброшенной через блок (рис.). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m1. С каким ускорением а движутся тела и каковы силы Т1 и Т2 натяжения нити по обе стороны от блока? Коэффициент трения f тела о поверность стола равен 0,2. Масса m блока равна 0,1 кг и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь.
Ответ:
![]() 1,96
м/с2,
1,96
м/с2,
![]() 0,98Н,
0,98Н,
![]() 1,18
Н.
1,18
Н.
B11. Платформа, имеющая форму диска, может вращатся около вертикальной оси. На краю платформы стоит человек массой m1 = 60 кг. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную точку на платформе? Масса m2 платформы равна 240 кг. Момент инерции J человека рассчитывать, как для материальной точки.
Ответ:
![]()
B12. Платформа в виде диска радиусом R = 1 м вращается по инерции с частотой n1 = 6 мин-1. На краю платформы стоит человек, масса m которого равна 80 кг. С какой частотой n2 будет вращатся платформа, если человек перейдет в ее центр? Момент инерции J платформы равен 120 кгм2. Момент инерции J человека рассчитывать, как для материальной точки.
Ответ: n2 = (J + mR2)n1/J = 10 мин-1.
