3.2.3. Синтез ких-фильтров

Наряду с БИХ-фильтрами широкое распространение получили цифровые фильтры с импульсной характеристикой конечной длительности, называемые иначе КИХ-фильтрами. КИХ-фильтры реализуются, как правило, по нерекурсивной схеме и обладают рядом положительных качеств, основное из которых состоит в том, что благодаря отсутствию обратных связей КИХ-фильтры всегда устойчивы. Кроме того, КИХ-фильтры могут иметь линейную фазо-частотную характеристику.

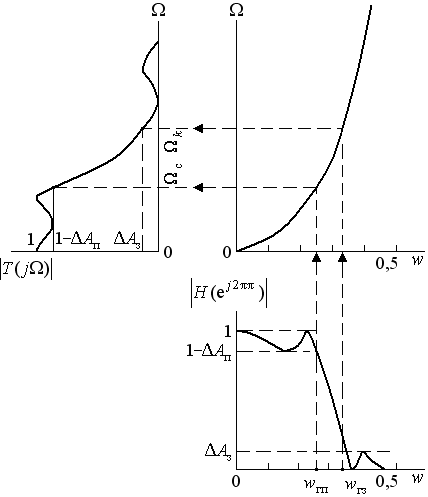
Рис. 3.4. Билинейное преобразование аналогового

фильтра-прототипа

Фильтры с конечной импульсной характеристикой не имеют непосредственных аналогов среди пассивных электрических фильтров, поэтому методы их синтеза относятся к прямым методам. Наиболее распространенными на практике методами синтеза ЦФ являются:

1. метод частотной выборки;

2. метод временных окон;

3. методы расчета оптимальных фильтров.

Метод частотной выборки

Одним из наиболее употребительных методов синтеза КИХ-фильтров является метод частотной выборки.

Идея метода очень проста. Частотную характеристику цифрового фильтра подвергают дискретизации как периодическую функцию, разбивая интервал по частоте () наравных частей. Интервал дискретизациидолжен быть таким, чтобы передать характерные подробности частотной характеристики. К образовавшейся последовательности значенийприменяют дискретное преобразование Фурье или быстрое преобразование Фурье и находят импульсную характеристику. Значенияявляются коэффициентами нерекурсивного фильтра.

Иногда получающаяся в процессе синтеза импульсная характеристика цифрового фильтра оказывается физически нереализуемой, так как отличны от нуля ее значения при отрицательных. Фильтр можно сделать физически реализуемым, если его импульсную характеристику сместить вправо так, чтобы для моментов времениона тождественно равнялась нулю. При таком смещении изменяется фазо-частотная характеристика цифрового фильтра, а его амплитудно-частотная характеристика остается неизменной. Поэтому метод частотной выборки позволяет синтезировать фильтры с заданной амплитудно-частотной характеристикой при неконтролируемой фазо-частотной характеристике.

Метод частотной выборки хорошо работает при плавных частотных характеристиках. Для фильтров с частотной характеристикой, имеющей резкие границы, процедура синтеза сильно усложняется и приводит к сильной изрезанности частотной характеристики и большому уровню боковых лепестков (рис. 3.5, а). При увеличении числа отсчетов степень изрезанности частотной характеристики не уменьшается, а только увеличивается частота биений.

Для уменьшения изрезанности частотной характеристики и уменьшения уровня боковых лепестков отсчетные значения частотной характеристики задают только в полосе пропускания фильтра, т.е. при и в полосе задерживания, а в промежуточной полосе их подбирают так, чтобы обеспечить наименьшую изрезанность частотной характеристики (рис. 3.5, б). Эта задача решается обычно на ЭВМ методом линейного программирования.

Метод временных окон

Еще один метод синтеза цифровых фильтров с конечной импульсной характеристикой основан на использовании так называемых временных окон.

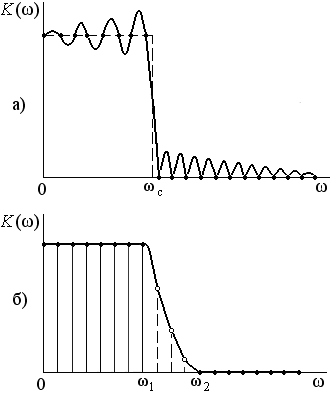
Рис. 3.5.Синтез ФНЧ с помощью метода частотной выборки:

а) частотная характеристика ФНЧ при формально произведенной дискретизации;

б) то же при подборе значений частотной характеристики в промежуточной полосе частот.

Рассмотрим идею метода временных окон на примере фильтра нижних частот.

Как известно, импульсная характеристика фильтра нижних частот с частотой среза ω₀ описывается функцией:

и имеет вид, изображенный на рис. 3.6, а. Такая импульсная характеристика физически нереализуема из-за того, что ее значения отличаются от нуля при отрицательных значениях . Чтобы сделать фильтр реализуемым, импульсную характеристику усекают с обеих сторон и смещают вправо, как показано на рис. 3.6, б.

Однако такое резкое усечение импульсной характеристики приводит к сильной изрезанности частотной характеристики в полосе пропускания и не допустимо большему уровню боковых лепестков в полосе задерживания (рис. 3.6. в). Чтобы улучшить вид частотной характеристики, необходимо импульсную характеристику умножить на весовую функцию (так называемое «временное окно») , которая близка к единице в середине и плавно убывает по краям. В результате форма импульсной характеристики становится более плавной и, как следствие этого, улучшается вид частотной характеристики.

Существует несколько различных типов временных окон. Одним из наиболее распространенных является окно Хемминга (рис. 3.6, г), которое описывается функцией:

.

Окно Хемминга позволяет получить частотную характеристику, близкую к прямоугольной, с уровнем боковых лепестков 53,6 дБ (рис. 3.6, д).

Однако наилучшие результаты получаются при использовании окна Кайзера, которое описывается выражением:

,

где – модифицированная функция Бесселя мнимого аргумента; – параметр окна, который выбирают, исходя из того, какое требование к частотной характеристике является более важным. При увеличении уменьшается уровень боковых лепестков частотной характеристики и пульсации в полосе пропускания, и в то же время уменьшается крутизна скатов частотной характеристики.

С помощью окна Кайзера можно синтезировать фильтры, имеющие практически прямоугольную форму частотной характеристики.