Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Уфимский государственный авиационный технический университет

Кафедра авиационного приборостроения

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ

Лабораторный практикум

по дисциплине

«Цифровая обработка сигналов»

Уфа 2006

Составители: В.И. Петунин, С.Т. Кадырова

УДК 681.3.06(07)

ББК 32.973(я7)

Цифровая обработка сигналов: Лабораторный практикум по дисциплине «Цифровая обработка сигналов» / Уфимск. гос. авиац. техн. ун-т; Сост. В.И. Петунин, С.Т. Кадырова. – Уфа, 2006. – 53 с.

Лабораторный практикум содержит основные сведения о спектрах сигналов, о характеристиках цифровых фильтров и о методах синтеза цифровых фильтров. Большое внимание уделяется вопросам анализа и синтеза цифровых БИХ- и КИХ-фильтров. Представлена подробная методика исследования цифровых фильтров с помощью интерактивной оболочки SPTool пакета Signal Processing системы MatLab.

Предназначен для студентов, обучающихся по направлению подготовки дипломированных специалистов 200100 «Приборостроение» и по специальности 200103 «Авиационные приборы и измерительно-вычислительные комплексы».

Табл. 2. Ил. 16. Библиогр.: 9 назв.

Рецензенты: д-р техн. наук, проф. Васильев В.И.

канд. техн. наук, доц. Беспалов А.И.

©Уфимский государственный

авиационный технический университет, 2006

СОДЕРЖАНИЕ

Введение 4

Лабораторная работа № 1. Спектральный анализ сигналов 5

Лабораторная работа № 2. Исследование характеристик

цифровых фильтров 20

Лабораторная работа № 3. Синтез цифровых БИХ- и КИХ-

фильтров 34

Список литературы 52

ВВЕДЕНИЕ

Цифровая обработка сигналов – обработка сигналов с помощью средств цифровой электронно-вычислительной техники.

Методы цифровой обработки сигналов впервые были использованы в 50-х годах ХХ века в радиолокационных станциях, в системах наведения и управления ракетами и космическими летательными аппаратами. Далее были разработаны устройства для цифровой обработки, заменяющие практически любые аналоговые устройства.

В настоящее время методы цифровой обработки сигналов широко применяются в радиотехнике, в системах связи, в системах управления и контроля.

Области применения цифровой обработки сигналов:

радио-, гидро- и звуколокация; сжатие данных в телеметрии; обнаружение сигналов в дальней космической связи; адаптивная коррекция сигналов связи; анализ и синтез речи; обработка фототелевизионной информации; цифровые методы измерения; моделирование динамических систем; обработка сигналов в геологоразведке, метрологии, сейсмологии, медицине и т.д.

Подобное широкое распространение методов определяется большими возможностями цифровой техники. С помощью цифровых устройств можно реализовывать очень сложные алгоритмы обработки сигналов. Причём алгоритмы обработки сигналов легко изменять в зависимости от вида сигналов. Следовательно, с помощью цифровых методов можно реализовать любой алгоритм цифровой обработки, который может быть описан совокупностью арифметических и логических операций.

В лабораторном практикуме рассмотрены три лабораторные работы:

лабораторная работа № 1 посвящена спектральному анализу сигналов;

лабораторная работа № 2 посвящена исследованию характеристик цифровых фильтров;

лабораторная работа № 3 посвящена синтезу цифровых БИХ- и КИХ-фильтров.

Исследование дискретных и цифровых систем проводится с помощью пакетов Signal Processing и Simulink системы Matlab.

ЛАБОРАТОРНАЯ РАБОТА № 1

Спектральный анализ сигналов

1.1. Цель работы

Целью данной работы является овладение навыками спектрального анализа сигналов.

1.2. Теоретическая часть

1.2.1. Математическое описание сигналов

Под сигналом понимают физический процесс, отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определенного типа.

Аналоговые сигналы (АС) описываются непрерывной (или кусочно-непрерывной) функцией , причем сама функция и аргумент могут принимать любые значения на некоторых интервалах времени. Пример АС: , , , вещественно, , приведен на рис. 1.1, а.

Аналоговые сигналы используются, например, в телефонии, радиовещании, телевидении.

Дискретные сигналы (ДС) описываются решетчатыми функциями, последовательностями – , где– интервал дискретизации,– целое,; сама функцияможет в дискретные моментыпринимать произвольные значения на некотором интервале. Эти значения функции называются выборками, или отсчетами функции. На рис. 1.1, б приведено графическое изображение ДС, , вещественно, Примером применения дискретных сигналов являются системы с амплитудно-импульсной модуляцией. Последовательностьможет быть и конечной, состоящей из определенного конечного числа отсчетов:,,; конечную последовательность можно записать в форме.

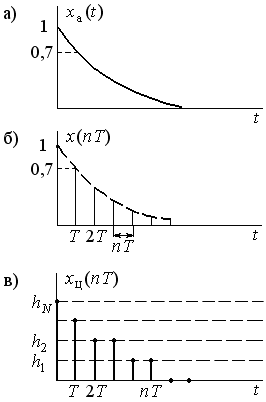
Рис. 1.1. Графическое изображение математических сигналов:

а) аналоговый сигнал; б) дискретный сигнал; в) квантованный

по уровню дискретный сигнал

Цифровые сигналы (ЦС) представляют собой квантованные по уровню дискретные сигналы и описываются квантованными решетчатами функциями (квантованными последовательностями) , принимающими в дискретные моментылишь конечный ряд дискретных значений – уровней квантования. Пример квантованного дискретного сигнала приведен на рис. 1.1, в. Связь между решетчатой функциейи квантованной решетчатой функциейопределяется нелинейной функцией квантования. Существуют различные способы выбора функции квантования. В простейшем случае, когда используется квантование с постоянным шагом , функция квантования имеет вид:

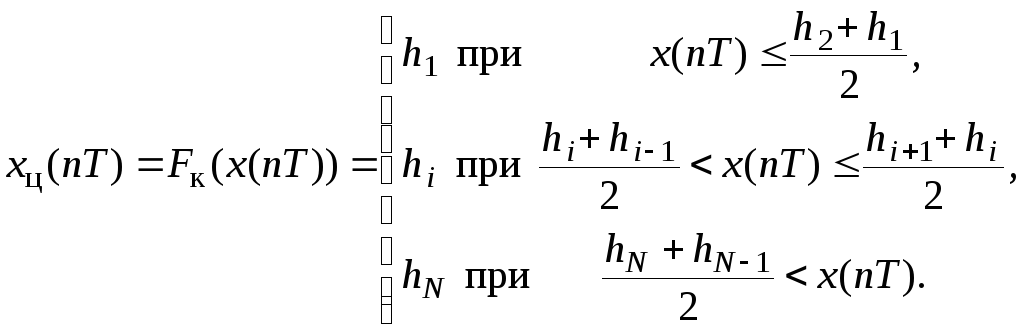(1.1)

Каждый из уровней квантования кодируется числом, обычно используются двоичные символы , и квантовые отсчетыкодируются двоичными числами сразрядами. Число уровней квантованияи наименьшее число разрядов двоичных чисел, кодирующих эти уровни, связаны соотношением:

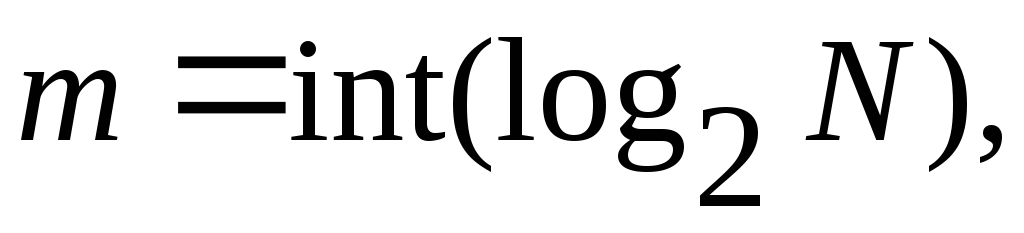(1.2)

где – наименьшее целое число, не меньшее числа.

Примеры дискретных сигналов

Рассмотрим некоторые широко используемые в теории цифровой обработки сигналов последовательности.

1. Сдвиг последовательности по осипоследовательность:

(1.3)

образуется при сдвиге последовательности наотсчетов вправо (при) или влево (при).

2. Дискретная дельта-функция (единичный импульс) определяется соотношением

(1.4)

3. Аналитическая запись последовательности. Из определения дискретной -функции следует, что любая последовательность может быть записана в виде:

(1.5)

так как все члены суммы при равны нулю.

4. Единичная последовательность определяется соотношением:

(1.6)

Заметим, что единичный импульс связан с единичной последовательностьюочевидными соотношениями:

(1.7)

. (1.8)

5. Экспоненциальная последовательность определяется соотношением:

, (1.9)

где в общем случае – комплексное число. При – вещественное число и– вещественная степенная последовательность.

6. Периодической называют последовательность , удовлетворяющую условию:

, (1.10)

где и– целые числа,;(или) – период последовательности.

Периодическую последовательность достаточно задать на интервале одного периода, например при . Из рассмотрения интервала одного периода (например, интервала) легко заметить, что при выходе в результате сдвига из интервала какого-то отсчета точно такой же отсчет входит в интервал с другого его конца. Такой сдвиг называется круговым.

1.2.2. Получение спектра сигнала

Спектром временной зависимости (функции) называется совокупность ее гармонических составляющих (гармоник), образующих ряд Фурье.

Спектральный анализ периодических функций заключается в нахождение коэффициентов и ряда Фурье:

, (1.11)

где – частота повторения (или частота первой гармоники),– номер гармоники.

Коэффициенты ряда Фурье определяются выражениями:

; (1.12)

, (1.13)

где – период повторения периодической функции.

Для описания аналоговых и дискретных сигналов в частотной области используется аппарат преобразования Фурье. Спектром аналогового сигналаназывают прямое преобразование Фурье:

. (1.14)

В свою очередь, согласно обратному преобразованию Фурье:

. (1.15)

Пара преобразований Фурье для решетчатой функции (дискретной последовательности) имеет вид:

; (1.16)

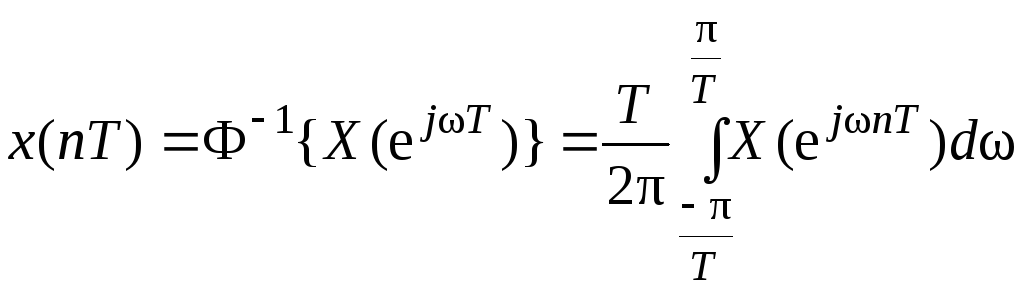, (1.17)

где – спектр дискретного сигнала.