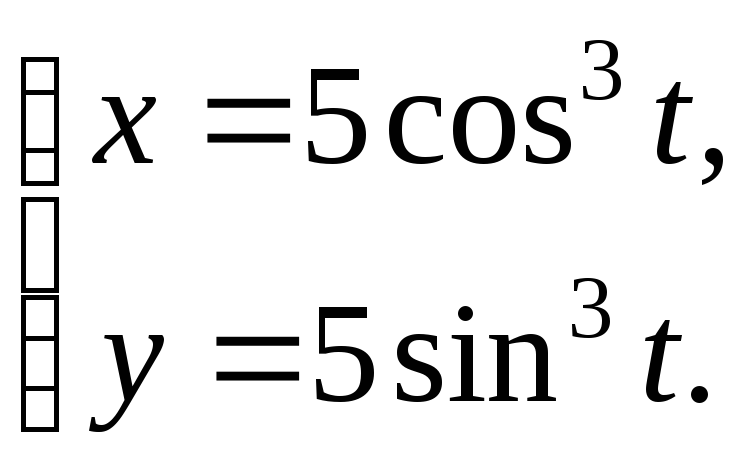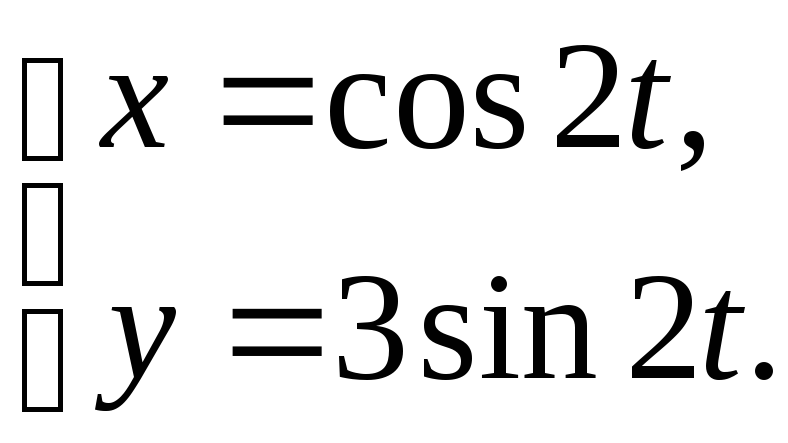Домашнее задание к практическому занятию № 9.
1. Построить кривую, заданную уравнением в полярной системе координат.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
2.
Построить кривую, заданную параметрическими
уравнениями
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
Решение типового варианта
1. Построить
кардиоиду, заданную уравнением в полярных
координатах
Решение:
Составим таблицу, в которой приведены
значения полярного угла
и соответствующие им значения полярного
радиуса
|
|
|
| |
|
0 |
4 |
| |
|
|
2 |
| |
|
|
|
| |
|
|
|
| |
|
|
0 |
| |
|
|
|
| |
|
|
|
| |
|
|
2 |
| |
|
|
4 |
| |
|
|
6 |
| |
|
|
|
| |
|
|
|
| |
|
|
8 |
| |
|
|
|
| |
|
|
|
| |
|
|
6 |
| |
|
Построив найденные
точки
|
Рис.4 | ||
1,2
0,6
0,6
1,2
6,8
7,4
7,4
6,8
в полярной системе координат (см.
пример 2) и соединив их плавной линией,
получим достаточно точное представление
о кардиоиде(рис.
4).
1. Построить кривую, заданную параметрическими уравнениями:
Выберем достаточное
количество значений параметра
вычислим соответствующие значения
и построим точки
в декартовых координатах. Соединим их
плавной линией. Очевидно, что полученная
кривая очень похожа на эллипс с полуосями
и центром в точке
Для строгого доказательства того, что
данные параметрические уравнения
определяют эллипс с указанными осями
и центром, избавимся от параметра
откуда
