Практические занятия матем / Практическое занятие 13

Практическое занятие 13

Односторонние пределы. Непрерывность

Задания:

Найти следующие односторонние пределы:

13.1. . 13.2. .

Ответ: Ответ:

13.3. . 13.4. .

Ответ: Ответ:

13.5. . 13.6. .

Ответ: Ответ:

13.7. . 13.8. .

Ответ: Ответ:

13.9. . 13.10. .

Ответ: Ответ:

13.11. . 13.12. а) .

Ответ: Ответ:

б) . Ответ:

Исследовать на непрерывность функции:

13.13. . 13.14. .

13.15. . 13.16. .

13.17. а) ; 13.18. .

б) .

13.19. . 13.20. .

13.21. . 13.22. .

13.23. . 13.24. .

13.25. . 13.26.

Построить график этой функции.

Задана функция . При каком выборе параметров, входящих в ее определение, будет непрерывной?

13.27.

Ответ:

13.28.

Ответ:

13.29.

Ответ:

Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию «по непрерывности»:

13.30. .

Ответ: точки разрыва второго рода.

13.31. .

Ответ: точка разрыва первого рода.

13.32. .

Ответ: точка устранимого разрыва,.

13.33. .

Ответ: точка устранимого разрыва,.

13.34. .

Ответ: точка устранимого разрыва,.

13.35. .

Ответ: точки разрыва второго рода.

13.36. .

Ответ: точка разрыва первого рода.

13.37. .

Ответ: точка разрыва первого рода.

13.38. .

Ответ: точка разрыва первого рода.

13.39. .

Ответ: точка устранимого разрыва, точка разрыва второго рода.

1340. .

Ответ: точка устранимого разрыва, точка устранимого разрыва, точка разрыва второго рода.

13.41. .

Ответ: точка устранимого разрыва, .

13.42.

Ответ: точка разрыва первого рода.

13.43. .

Ответ: точка разрыва первого рода.

13.44.

Ответ: точка разрыва первого рода.

13.45.

Ответ: точка разрыва первого рода.

Дополнительные сведения.

1. Непрерывность функции в точке. Классификация точек разрыва. Функция с областью определения называется непрерывной в точке , если выполнены следующие три условия:

а) функция определена в точке , т.е. ;

б) существует ;

в) .

Если а) выполнено, то условия б) и в) эквивалентны следующему:

,

где

– приращение функции в точке , соответствующее приращению аргумента .

Если в точке нарушено хотя бы одно из условий а)-в), то называется точкой разрыва функции . При этом различают следующие случаи:

а) существует, но функция не определена в точке или нарушено условие . В этом случае называется точкой устранимого разрыва функции.

б) не существует. Если при этом существуют оба односторонних предела и (очевидно, не равные друг другу), то называется точкой разрыва 1-го рода.

в) в остальных случаях называется точкой разрыва 2-го рода.

2. Односторонние пределы. Если и , то условно пишут ; аналогично, если и , то это записывается так: . Числа

и

называются соответственно пределом слева функции в точке и пределом справа функции в точке (если эти числа существуют).

Для существования предела функции при необходимо и достаточно, чтобы имело место равенство

.

Пример 1. Доказать, что функция

непрерывна для любого аргумента .

Решение:

Имеем:

.

Так как

и ,

то при любом имеем

.

Следовательно, функция непрерывна при .

Пример 2. Найти пределы справа и слева функции

при .

Решение:

Имеем:

и

.

Предела же функции при в этом случае, очевидно, не существует.

Пример 3. Найти левый и правый пределы функции

при .

Решение:

Если , то и . Следовательно, .

Если же , то , и .

Пример 4. Найти левый и правый пределы функции

при .

Решение:

Если , то и .

Если же , то и .

Пример 5. Показать, что при функция имеет разрыв.

Решение:

Находим , . Таким образом, функция при не имеет ни левого, ни правого конечного предела. Следовательно, является точкой разрыва II рода.

Пример 6. Показать, что при функция имеет разрыв.

Решение:

Если , то и . Если же , то и . Итак, при функция имеет как правый так и левый конечный предел, причем эти пределы различны. Следовательно, является точкой разрыва I рода – точкой скачка. Скачок функции в этой точке равен .

Домашнее задание к практическому занятию № 13.

1. Исследовать данные функции на непрерывность и построить их графики.

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14) .

15) 16)

17) 18)

19) 20)

21) 22)

23) 24)

25) 26)

27) 28)

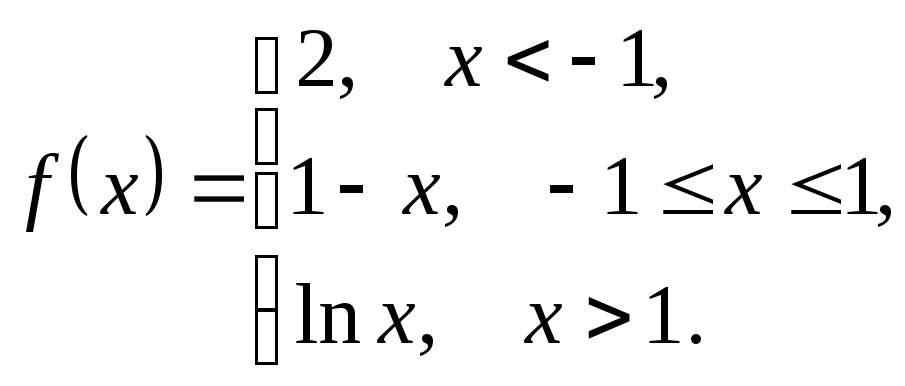29) 30)

2. Исследовать данные функции на непрерывность в указанных точках.

1) .

2) .

3) .

4) .

5) .

6) .

7) .

8) .

9) .

10) .

11) .

12) .

13) .

14) .

15) .

16) .

17) .

18) .

19) .

20) .

21) .

22) .

23) .

24) .

25) .

26) .

27) .

28) .

29) .

30) .

Решение типового варианта

1. Исследовать данную функцию на непрерывность и построить ее график:

Функция определена и непрерывна на интервалах и , где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках и . Для точки имеем:

,

т.е. функция в точке имеет разрыв первого рода.

Для точки находим:

, , т.е. в точке функция также имеет разрыв первого рода. График данной функции изображен на рис.1.

Рис.1.

2. Исследовать функцию на непрерывность в точках .

Для точки имеем:

,

,

т.е. в точке функция терпит бесконечный разрыв (–точка разрыва второго рода).

Для точки имеем:

,

.

Следовательно, в точке функция непрерывна.

258