Практическое занятие 7 Плоскость и прямая в пространстве

Задания:

7.1. Заданы плоскость и точка. Написать уравнение плоскости, проходящей через точкупараллельно плоскости, и вычислить расстояние, если:

1) .

2) .

Ответ: 1) . 2), плоскость параллельна осии проходит через начало координат;.

7.2. Написать уравнение плоскости , проходящей через заданные точкииперпендикулярно заданной плоскости, если:

1) ;

2) .

Ответ: 1) ; 2).

7.3. Написать уравнение плоскости, проходящей через точку параллельно векторами, если:

1) ;

2) .

Ответ: 1) ; 2).

7.4. Написать уравнение плоскости, проходящей через точки

и , параллельно вектору, если:

1) ;

2) .

Ответ: 1) ; 2).

7.5. Написать уравнение плоскости, проходящей через точки

,и, если:

1) ;

2) .

Ответ: 1) ; 2).

В задачах 7.6-7.9 исследовать взаимное расположение заданных плоскостей. При этом в случае найти расстояние

между плоскостями, а в случае пересечения и– косинус угла между ними.

7.6. .

Ответ: Пересекаются, .

7.7. .

Ответ: Параллельны, .

7.8. .

Ответ: Пересекаются, .

7.9. .

Ответ: Совпадают.

7.10. Вычислить объем пирамиды, ограниченной плоскостью и координатными плоскостями.

Ответ: 8.

7.11. Написать уравнение плоскости, проходящей через точку и отсекающей от осей координат положительные и равные отрезки.

Ответ: .

7.12. Три грани тетраэдра, расположенного во втором октанте , совпадают с координатными плоскостями. Написать уравнение четвертой грани, зная длину ребер, ее ограничивающих:, и найти длину высотытетраэдра.

Ответ: .

7.13. Написать уравнения плоскостей, делящих пополам двугранные углы, образованные плоскостями и, если:

1) ;

2) .

Ответ: 1) и;

2) и.

7.14. Написать уравнение плоскости, равноудаленной от двух заданных плоскостей и, если:

1) ;

2) .

Ответ: 1) ; 2).

7.15. Установить, лежат ли точки ив одном угле, в смежных или в вертикальных углах, образованных плоскостямии, если:

1) ;

2) .

Ответ: 1) в смежных углах; 2) в одном углу.

7.16. Известны координаты вершин тетраэдра: ,,,. Написать уравнения его граней.

Ответ:

7.17. Составить уравнение плоскости, проходящей через точку и перпендикулярной к плоскостями.

Ответ: .

7.18. Прямая задана общими уравнениями. Написать для этой прямой канонические уравнения и уравнения в проекциях, если:

1) 2)

Ответ: 1) канонические уравнения, уравнения в проекциях:

2) ,уравнения в проекциях:

7.19. Написать канонические уравнения прямой, проходящей через точку параллельно:

1) вектору ;

2) прямой ;

3) оси ;

4) оси ;

5) прямой ;

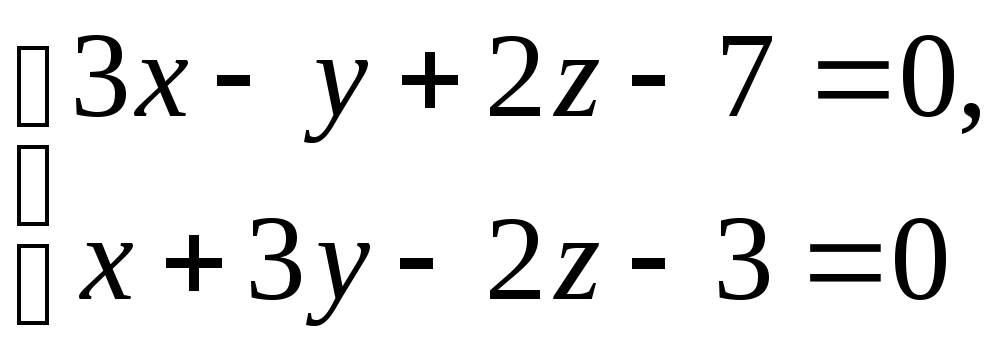6) прямой .

Ответ: 1) ; 2);

3) ; 4);

5) ; 6) .

7.20. Написать уравнение прямой, проходящей через две заданные точки и, если:

1) ;

2) .

Ответ: 1) ;

2) .

7.21. Заданы прямая и точка(проверить!). Требуется:

1) написать уравнение плоскости, проходящей через прямую и точку;

2) написать уравнение плоскости, проходящей через точку

перпендикулярно прямой ;

3) написать уравнение перпендикуляра, опущенного из точки на прямую;

4) вычислить расстояние ;

5) найти проекцию точки на прямой.

Ответ: 1) ; 2) ;

3) или;

4) ; 5)

7.22. Найти расстояние между параллельными прямыми и.

Ответ: 3.

7.23. Найти расстояние от точки до заданной прямой:

1) 2)

Ответ: 1) ; 2) 21.

7.24. Доказать, что прямые 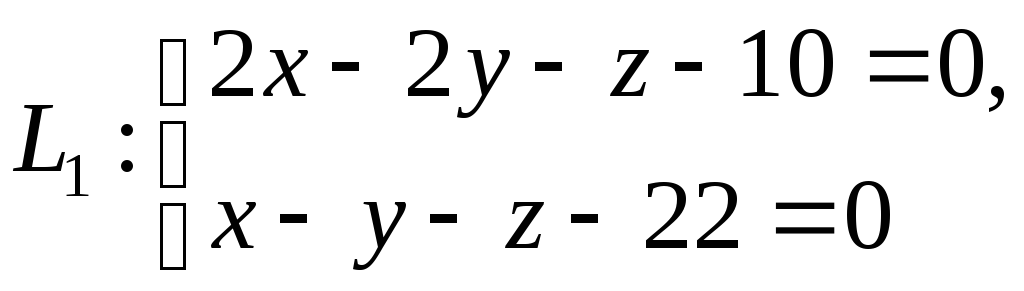ипараллельны и найти расстояние.

Ответ: 25.

7.25. Составить уравнение прямой, проходящей через точки пересечения плоскости с прямымии.

Ответ: .

7.26. При каком значении плоскостьбудет параллельна прямой

Ответ: –11.

7.27. Найти уравнения проекции прямой на плоскость.

Ответ: .

7.28. Определить угол между прямой и плоскостью проходящей через точки,,.

Ответ: .

7.29. Написать уравнение прямой, проходящей через точку параллельно плоскостии пересекающей прямую.

Ответ: .

7.30. Написать каноническое уравнения прямой, которая проходит через точку параллельно плоскостии пересекает прямую.

Ответ: .