Домашние задания к практическому занятию №4.

1. Даны векторы и, где;;. Найти: а); б); в).

1) ,,,,,,,,,,.

Ответ: а) 2834.

2) ,,,,,,,,,,

Ответ: а) – 950.

3) ,,,,,,,,,,

Ответ: а) – 1165.

4) ,,,,,,,,,,.

Ответ: а) 416.

5) ,,,,,,,,,,.

Ответ: а) 750.

6) ,,,,,,,,,,.

Ответ: а) – 2116.

7) ,,,,,,,,,,.

Ответ: а) 165.

8) ,,,,,,,,,,.

Ответ: а) – 583.

9) ,,,,,,,,,,.

Ответ: а) 1287.

10) ,,,,,,,,,,.

Ответ: а) 2337.

11) ,,,,,,,,,,.

Ответ: а) – 936.

12) ,,,,,,,,,,.

Ответ: а) 320.

13) ,,,,,,,,,,.

Ответ: а) 352.

14) ,,,,,,,,,,.

Ответ: а) 1809.

15) ,,,,,,,,,,.

Ответ: а) – 5962.

16) ,,,,,,,,,,.

Ответ: а) 3348.

17) ,,,,,,,,,,.

Ответ: а) – 2076.

18) ,,,,,,,,,,.

Ответ: а) 1728.

19) ,,,,,,,,,,.

Ответ: а) 1044.

20) ,,,,,,,,,,.

Ответ: а) 1994.

21) ,,,,,,,,,,.

Ответ: а) 29767.

22) ,,,,,,,,,,.

Ответ: а) 20758.

23) ,,,,,,,,,,.

Ответ: а) 2751.

24) ,,,,,,,,,,.

Ответ: а) 38587.

25) ,,,,,,,,,,.

Ответ: а) 1048.

26) ,,,,,,,,,,.

Ответ: а) 2532.

27) ,,,,,,,,,,.

Ответ: а) 21156.

28) ,,,,,,,,,,.

Ответ: а) –12200.

29) ,,,,,,,,,,.

Ответ: а) –2916.

30) ,,,,,,,,,,.

Ответ: а) –801.

2. По координатам точек идля указанных векторов найти: а) модуль вектора; б) скалярное произведение векторови; в) проекцию векторана вектор; г) координаты точки, делящей отрезокв отношении.

1) , , , , , , , .

Ответ: а) ; б) 314; г).

2) , , ,, , , ,.

Ответ: а) ; б) –50; г).

3) , , ,, , , ,.

Ответ: а) ; б) –53; г).

4) , , ,, , , ,.

Ответ: а) ; б) –53; г).

5) , , ,, , , ,.

Ответ: а) 11; б) –20; г) .

6) , , , , , , ,.

Ответ: а); б)70; г).

7) , , ,, , , ,.

Ответ: а) ; б) 4; г).

8) , , , , , ,.

Ответ: а); б) –29; г).

9) , , , , , ,.

Ответ: а); б) –294; г).

10) , , , , , ,.

Ответ: а); б) –420; г).

11) , , , , , ,.

Ответ: а); б) 80; г).

12) , , , , , ,.

Ответ: а); б) 238; г).

13) , , , , , ,.

Ответ: а); б) –160; г).

14) , , , , , ,.

Ответ: а); б) –298; г).

15) , , ,, , , ,.

Ответ: а); б) 94; г).

16) , , , , , ,.

Ответ: а); б) 554; г).

17) , , , , , ,.

Ответ: а); б) –263; г).

18) , , , , , ,.

Ответ: а); б) 986; г).

19) , , , , , ,.

Ответ: а); б) –1308; г).

20) , , ,, , , ,.

Ответ: а); б) 1185; г).

21) , , ,, , , ,.

Ответ: а); б) –487; г).

22) , , , , , ,.

Ответ: а); б) 1549; г).

23) , , , , , ,.

Ответ: а); б) –1120; г).

24) , , , , , ,.

Ответ: а); б) –434; г).

25) , , , , , ,.

Ответ: а); б) –487; г).

26) , , , , , , ,.

Ответ: а); б) 697; г).

27) , , , , , ,.

Ответ: а); б) 396; г).

28) , , , , , , ,.

Ответ: а); б) 470; г).

29) , , , , , , ,.

Ответ: а); б) –85; г).

30) , , , , , ,.

Ответ: а); б) –40; г).

3. Доказать, что векторы ,,образуют базис, и найти координаты векторав этом базисе.

1) .

Ответ: (3, 2, –1).

2) .

Ответ: (–1, 2, 2).

3) .

Ответ: (2, 3, –4).

4) .

Ответ: (2, –1, 3).

5) .

Ответ: (2, 3, –1).

6) .

Ответ: (2, –2, 1).

7) .

Ответ: (2, 3, 4).

8) .

Ответ: (–1, 28, 4).

9) .

Ответ: (2, –1, 3).

10) .

Ответ: (–1, 2, 1).

11) .

Ответ: (2, 4, –5).

12) .

Ответ: (2, 1, –3).

13) .

Ответ: (1, –2, –3).

14) .

Ответ: (0, 2, –3).

15) .

Ответ: (3, 4, –5).

16) .

Ответ: (12, 1, –1).

17) .

Ответ: (2, 3, 1).

18) .

Ответ: (2, –3, –1).

19) .

Ответ: (5, 2, –1).

20) .

Ответ: (-1, 2, –3).

21) .

Ответ: (–1, 3, 2).

22) .

Ответ: (2, –1, 3).

23) .

Ответ: (3, –1, 2).

24) .

Ответ: (3, 2, –1).

25) .

Ответ: (2, 0, 4).

26) .

Ответ: (–1, 5, 2).

27) .

Ответ: (3, 4, –1).

28) .

Ответ: (–2, 3, 2).

29) .

Ответ: (2, –1, 1).

30) .

Ответ: (1, 1, –2).

Решение типового варианта

1. Даны векторы и, где. Найти: а); б); в).

Решение.

а) Вычисляем

б) Пусть . Тогда

,

.

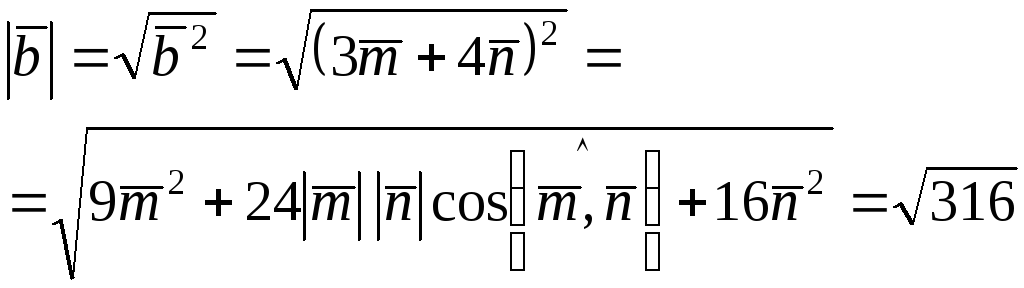Окончательно получаем

;

в) Пусть .

Тогда

,

,

,

.

В результате имеем:

.

2. По координатам точек инайти: а) модуль вектора; б) скалярное произведение векторови; в) проекцию векторана вектор; г) координаты точки, делящей отрезокв отношении.

Решение:

а) Последовательно находим ,,,

;

б) Имеем . Тогда

;

в) Так как

,

,

то

;

г) Имеем: . Следовательно,

;

.

3. Доказать, что векторы образуют базис, и найти координаты векторав этом базисе.

Решение:

Вычисляем

.

Следовательно, векторы образуют базис, и векторлинейно выражается через базисные векторы:

или в координатной форме

Решаем полученную систему по формулам Крамера.

Находим: ,

,

,

откуда , поэтому

.

81