Практические занятия матем / Практическое занятие 2
.docПрактическое занятие 2
Матрицы
Задания:
2.1. Даны
матрицы
и
.
Найти:
,
если:
1)
;
2)
.
Ответы:
1)
,
;
2)
,
,
2.2.
Даны матрицы
и
.
Найти:
,
если:
1)
;
2)
;
3)
;
4)
;
5)
.
Ответ:
1)
,
;
2)
;
3)
;
4)
;
5)
.
2.3.
Даны матрицы
найти все перестановочные (коммутирующие)
с ней квадратные матрицы
.
Проверить выполняемость равенства
,
если:
1)
; 2)
.
Ответ:
1)
;
2)
,
где
любые
числа (параметры).
2.4.
Даны матрицы
,
и
.
Найти
и показать, что
,
если:
1)
;
2)
Ответ:
1)
;
2)
.
2.5. Методом присоединений матрицы найти обратные для следующих матриц:
1)
. 2)
. 3)
.
4)
. 5)
. 6)
.
Ответ:
1)
.
2)
3)
. 4)
.
5)
. 6)
.
2.6. Методом элементарных преобразований найти обратные для следующих матриц:
1)
.
2)
.
3)
.
4)
.
5)
.
Ответ:
1)
.
2)
3)
.
4)
.
5)
.
2.7. Решить матричные уравнения:
1)
.
2)
.
3)
.
4)
.
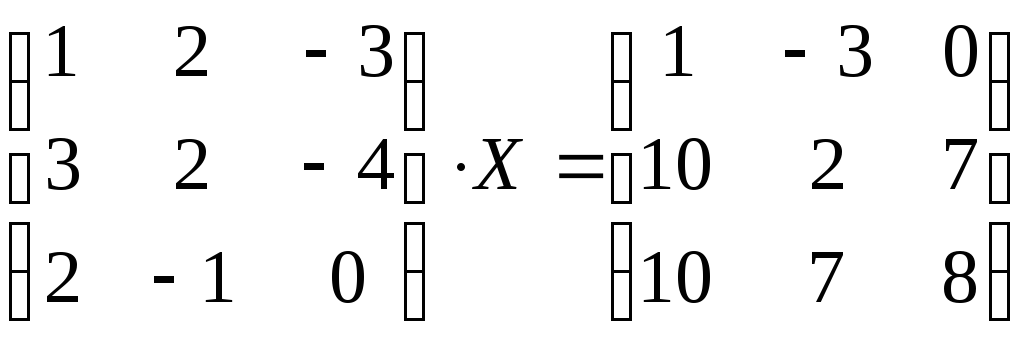5)
.
Ответ:
1)
.
2)
.
3)
.
4)
. 5)
.
Дополнительные сведения.
1. Операции над матрицами.
Матрицей
размера mn
или (mn)
–
матрицей
называется прямоугольная таблица из
чисел
состоящая из
строк и
столбцов.
Число строк
(столбцов) квадратной матрицы будем
называть порядком матрицы.
Суммой
–
матриц
и
называется матрица
того же размера, каждый элемент которой
равен сумме соответственных элементов
матриц
и
:
.
Произведением
матрицы
на число
(действительное или комплексное)
называется матрица
,
получающаяся из матрицы
умножением ее элементов на
:
.
Произведением
-матрицы
на
-матрицу
называется
-матрица
,
элемент которой
,
стоящий в
-й
строке и в
-м
столбце, равен сумме произведений
соответственных элементов
-й
строки матрицы
и
-го
столбца матрицы
:
.
2.
Обратная матрица. Квадратная
матрица
называется вырожденной
(особенной), если ее определитель равен
нулю, и невырожденной
(неособенной) в противном случае. Если
– невырожденная матрица, то существует
и притом единственная матрица
такая, что
,
где
– единичная матрица (т.е. такая, на
главной диагонали которой стоят единицы,
а все остальные элементы равны нулю).
Матрица
называется обратной
к матрице
.
Укажем основные методы вычисления обратной матрицы.
Метод
присоединенной матрицы.
Присоединенная матрица
определяется как транспонированная к
матрице, составленной из алгебраических
дополнений соответствующих элементов
матрицы
.
Таким образом,
.
Справедливо равенство
.
Отсюда следует,
что если
– невырожденная
матрица, то
.
Пример
1. Методом
присоединенной матрицы найти
,
если
.
Решение:
Имеем
.
Найдем алгебраические дополнения
соответствующих элементов матрицы
:
Поэтому
и
.
Метод элементарных преобразований. Элементарным преобразованием матрицы называются следующее:
-
перестановка строк (столбцов);
-
умножение строки (столбца) на число, отличное от нуля;
-
прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.
Для данной матрицы
-го
порядка построим прямоугольную матрицу
размера
,
приписывая к
справа единичную матрицу. Далее, используя
элементарные преобразования над
строками, приводим матрицу
к виду
,
что всегда возможно, если
невырождена. Тогда
.
Пример
2. Методом
элементарных преобразований найти
для
.
Образуем матрицу
:
.
Обозначив через
строки матрицы
,
произведем над ними следующие
преобразования:
В результате последовательно получаем
Следовательно
Домашнее задание к практическому занятию № 2.
Даны матрицы
и
.
Найти:
а)
; б)
; в)
; г)
; д)
.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
,
.
16)
.
17)
.
18)
.
19)
.
20)
.
21)
.
22)
.
23)
.
24)
.
25)
.
26)
.
27)
.
28)
.
29)
.
30)
.
Решение типового варианта
Даны две матрицы:
.
Найти: а)
;
б)
;
в)
;
г)
;
д)
.
Решение:
а) Произведение
имеет смысл, так как число столбцов
матрицы
равно числу строк матрицы
.
Находим матрицу
,
элементы которой
.
Имеем:
;
б) Вычислим
.
Очевидно, что
;
в) Обратная матрица
матрицы
имеет вид (см. формулу выше)
где
т.е. матрица
– невырожденная, и, значит, существует
матрица
.
Находим:
Тогда
г) Имеем:
д) Имеем:
т.е. обратная матрица найдена верно.