3. Практические задачи на экстремум

Пример 13. Каковы должны быть размеры (радиус основания и высота) открытого сверху цилиндрического бака максимальной вместимости, если для его изготовления отпущеномматериала?

Решение: Вместимость бака а на его изготовление пойдет материал площадьюОтсюда определяем высоту бака

Тогда вместимость бака

Найдем то значение при котором вместимостьбудет максимальной. Имеем:

м.

Так как то при найденном значениивместимость бака будет максимальной.

Высота бак находится из полученного выше соотношения:

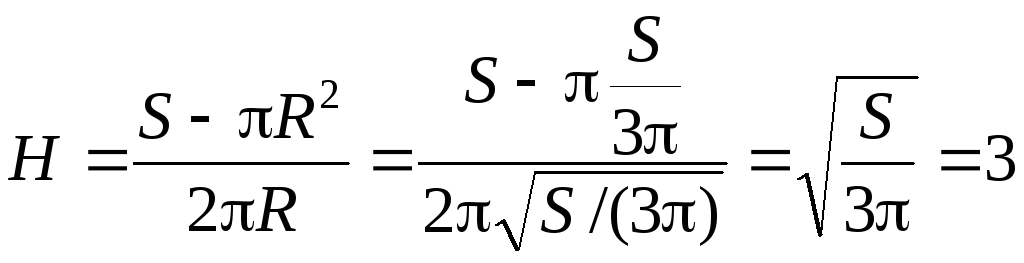м.

Домашнее задание к практическому занятию № 17

1. Решить следующие задачи.

1) Записать уравнение касательной к кривой в точке с абсциссой

2) Записать уравнение нормали к кривой в точке с абсциссой

3) Записать уравнение касательной к линии в точке с абсциссой

4) Записать уравнение касательной к линии в точке с абсциссой

5) Записать уравнение касательной к кривой в точке

6) Записать уравнение нормали к кривой в точке

7) Определить угловой коэффициент касательной к кривой в точке

8) В какой точке кривой касательная перпендикулярна к прямой?

9) Записать уравнение касательной к кривой в точке с абсциссой

10) Записать уравнение касательной к кривой в точке с абсциссой

11) Записать уравнение нормали к кривой в точке с абсциссой

12) Записать уравнение касательной к кривой в точке с абсциссой

13) Записать уравнение нормали к кривой в точке с абсциссой

14) Записать уравнение касательной к кривой в точке с абсциссой

15) Записать уравнение нормали к кривой в точке с абсциссой

16) Записать уравнение касательной к кривой в точке с абсциссой

17) Выяснить, в каких точках кривой касательная составляет с осьюугол

18) Выяснить, в какой точке кривой касательная составляет с осьюугол

19) Выяснить, в какой точке кривой касательная составляет с осьюугол

20) Выяснить, в каких точках кривой касательная составляет с осьюугол

21) Найти точки на кривой в которых касательные параллельны оси.

22) Найти точку на кривой касательная в которой параллельна прямой

23) Найти точку на кривой касательная в которой перпендикулярна к прямой

24) Найти точку на кривой касательная в которой параллельна прямой

25) Найти точку на кривой касательная в которой перпендикулярна к прямой

26) Найти точку на кривой касательная в которой параллельна прямой

27) Найти точку на кривой касательная в которой параллельна прямой

28) Выяснить, в какой точке кривой касательная параллельна прямой

29) Выяснить, в какой точке кривой касательная перпендикулярна к прямой

30) Выяснить, в какой точке кривой касательная параллельна прямой

2. Решить следующие задачи.

1) Траектория движения тела – кубическая парабола В каких ее точках скорости возрастания абсциссы и ординаты одинаковы?

Ответ:

2) Закон движения материальной точки в какой момент времени скорость ее движения будет равна 2 м/с?

Ответ: 10/3 с.

3) По оси движутся две материальные точки, законы движения которыхиC какой скоростью эти точки удаляются друг от друга в момент встречи?

Ответ: 40 м/с или 26 м/с.

4) Материальная точка движется по гиперболе так, что ее абсциссаравномерно возрастает со скоростью 1 м/с. С какой скоростью изменяется ордината точки, когда она проходит положение (6, 2)?

Ответ: –1/3 м/с.

5) В какой точке параболы ордината возрастает вдвое быстрее, чем абсцисса?

Ответ: (1/4, 1).

6) Закон движения материальной точки Найти скорость движения точки в момент временис.

Ответ: 22 м/с.

7) Закон движения материальной точки Найти скорость ее движения в момент временис.

Ответ: 100 м/с.

8) Закон движения материальной точки . Найти ее скорость в момент временис.

Ответ: –1 м/с.

9) Закон движения материальной точки . Найти ее скорость в момент временис.

Ответ: /2 м/с.

10) Закон движения материальной точки . Найти ее скорость в момент временис.

Ответ: 3/8 м/с.

11) Закон движения материальной точки . В какой момент времени ее скорость будет равна 42м/с?

Ответ: 3с.

12) Закон движения материальной точки . В какой момент времени ее скорость будет равна 190 м/с?

Ответ: 4 с.

13) Закон движения материальной точки . Найти скорость ее движения в момент временис.

Ответ: 78 м/с.

14) Закон движения материальной точки . Найти скорость ее движения в момент временис.

Ответ: 88 м/с.

15) По оси движутся две материальные точки, законы движения которыхи. С какой скоростью удаляются эти точки друг от друга в момент встречи?

Ответ: 42 м/с, 33 м/с.

16) По оси движутся две материальные точки, законы движения которыхи. С какой скоростью удаляются эти точки друг от друга в момент встречи?

Ответ: 39 м/с, 32 м/с.

17) По оси движутся две материальные точки, законы движения которыхи. В какой момент времени их скорости окажутся равными?

Ответ: 6 с.

18) Закон движения материальной точки . В какой момент времени скорость ее движения будет равна 10 м/с?

Ответ: 7 с.

19) Материальная точка движется по гиперболе так, что ее абсцисса равномерно возрастает со скоростью 1м/с. С какой скоростью изменяется ее ордината, когда точка проходит положение (4;5)?

Ответ: – 1,25 м/с.

20) В какой точке параболы ордината возрастает вдвое быстрее, чем абсцисса?

Ответ: .

21) По оси движутся две материальные точки, законы движения которыхи. С какой скоростью удаляются эти точки друг от друга в момент встречи?

Ответ: 42 м/с или 35 м/с.

22) В какой точке кривой ордината возрастет в четыре раза быстрее, чем абсцисса?

Ответ: .

23) В какой точке параболы абсцисса возрастает вдвое быстрее, чем ордината?

Ответ: .

24) В какой точке параболы абсцисса возрастает в пять раз быстрее, чем ордината?

Ответ: (1; 0,1).

25) По оси движутся две материальные точки, законы движения которыхи. В какой момент времени их скорости будут равными?

Ответ: 4с.

26) Закон движения материальной точки по прямой задан формулой . В какой момент времени скорость точки будет равна нулю?

Ответ: 78 м/с.

27) Тело движется по прямой по закону. Определить скорость и ускорение движения тела. В какие моменты времени оно меняет направление движения?

Ответ: 2с, 5с.

28) Зависимость между массой кг. вещества, получаемого в некоторой химической реакции, и временемвыражается уравнением. Определить скорость реакции, в случае, когдас.

Ответ: 28кг/с.

29) Материальная точка движется прямолинейно так, что , гдескорость,пройденный путь. Определить ускорение движения точки в момент, когда скорость равна 6м/с.

Ответ: .

30) Закон движения материальной точки . Найти скорость ее движения в момент временис.

Ответ: 15 м/с.

3. Решить следующие задачи:

1) Полотняный шатер объемом имеет форму прямого конуса. Каково должно быть отношение высоты конуса к радиусу его основания, чтобы на шатер пошло наименьшее количество полотна?

Ответ:

2) В равнобедренный треугольник с основанием и углом при основаниивписать параллелограмм наибольшей площадью так, чтобы одна из его сторон лежала на основании, а другая на боковой стороне треугольника. Найти длины сторон параллелограмма.

Ответ: и

3) Найти соотношение между радиусом и высотойцилиндра, имеющего приданном объеменаименьшую полную поверхность.

Ответ:

4) Требуется сделать коническую воронку с образующей, равной 20см. Какой должна быть высота воронки, чтобы ее объем был наибольшим?

Ответ: см.

5) Периметр равнобедренного треугольника равен Каково должно быть его основание, чтобы объем тела, образованного вращением этого треугольника вокруг его основания, был наибольшим?

Ответ:

6) Найти высоту конуса наибольшего объема, который можно вписать в шар радиусом

Ответ:

7) Проволокой, длина которой м, необходимо огородить клумбу, имеющую форму кругового сектора. Каким должен быть радиус круга, чтобы площадь клумбы была наибольшей?

Ответ: м.

8) Определить наибольшую площадь прямоугольника, вписанного в полукруг радиусом

Ответ:

9) Бревно длиной 20 м имеет форму усеченного конуса, диаметры оснований которого равны 2 м и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна, а объем был бы наибольшим. Каковы должны быть размеры балки?

Ответ: длина балки м, сторона поперечного сечениям.

10) С корабля, который стоит на якоре в 9 км от берега, нужно послать гонца в лагерь, расположенный в 15 км от ближайшей к кораблю точки берега. Скорость посыльного при движении пешком – 5 км/ч, а на лодке – 4 км/ч. В каком месте он должен пристать к берегу, чтобы попасть в лагерь в кратчайшее время?

Ответ: в 3 км от лагеря.

11) Полоса жести шириной , имеющая прямоугольную форму, должна быть согнута в виде открытого кругового цилиндрического желоба так, чтобы его сечение имело форму сегмента. Каким должен быть центральный угол, опирающийся на дугу этого сегмента, чтобы вместимость желоба была наибольшей?

Ответ: .

12) Из круглого бревна диаметром надо вырезать балку прямоугольного сечения. Каковы должны быть ширинаи высотаэтого сечения, чтобы балка, будучи горизонтально расположенной и равномерно нагруженной, имела наименьший прогиб? (Величина прогиба обратно пропорциональна произведению шириныпоперечного сечения и куба высоты.)

Ответ: .

13) Стоимость железнодорожной перевозки груза на 1 км () равна., а автомобильной. В каком местенадо начать строительство шоссе, чтобы возможно дешевле доставлять груз из пунктав? Известно, что(рис.1).

Ответ: на расстоянии от точки.

Рис.1

14) Человеку нужно добраться из пункта , находящегося на одном берегу реки, в пунктна другом ее берегу. Зная, что скорость движения по берегу враз больше скорости движения по воде, определить, под каким углом человек должен пересечь реку, чтобы достичь пунктав кратчайшее время. Ширина реки, расстояние между пунктамии(вдоль берега) равно.

Ответ: .

15) На прямолинейном отрезке , соединяющем два источника света:(силой) и(силой), найти точку, освещаемую слабее всего, если. (Освещенность обратно пропорциональна квадрату расстояния от источника света.)

Ответ: на расстоянии от точки.

16) Лампа висит над центром круглого стола радиусом . При какой высоте лампы над столом освещенность предмета, лежащего на его крае, будет наилучшей? (Освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света.)

Ответ:

17) Из всех цилиндров, вписанных в данный конус, найти тот, у которого боковая поверхность наибольшая. Высота конуса , радиус основания.

Ответ: радиус основания цилиндра , высота.

18) Из бумажного круга вырезан сектор, а из оставшейся его части склеена коническая воронка. Какой угол должен иметь вырезанный сектор, чтобы объем воронки был наибольшим?

Ответ:

19) Из всех конусов с данной боковой поверхностью найти тот, у которого объем наибольший.

Ответ: радиус основания конуса высота

20) Пункт находится на расстоянии 60 км от железной дороги. Расстояние по железной дороге от пунктадо ближайшей к пунктуточкисоставляет 285 км. На каком расстоянии от точкинадо построить станцию, от которой проложат шоссе к пунктучтобы затрачивать наименьшее время на передвижения между пунктамии, если скорость движения по железной дороге равна 52 км/ч, а скорость движения по шоссе – 20 км/ч.

Ответ: 25 км.

21) Канал, ширина которого м, под прямым углом впадает в другой канал ширинойм. Определить наибольшую длину бревен, которые можно сплавлять по этой системе каналов.

Ответ: м.

22) Найти высоту прямого кругового конуса наименьшего объема, описанного около шара радиусом

Ответ:

23) При каком наклоне боковых сторон равнобедренной трапеции площадь ее будет наибольшей, если боковые стороны равны а меньшее основание

Ответ:

24) Из фигуры, ограниченной кривой и прямымивырезать прямоугольник наибольшей площадью.

Ответ:

25) Равнобедренный треугольник, вписанный в окружность радиусом , вращается вокруг прямой, которая проходит через его вершину параллельно основанию. Какой должна быть высота этого треугольника, чтобы тело, полученное в результате его вращения, имело наибольший объем?

Ответ:

26) Требуется изготовить открытый цилиндрический бак вместимостью Стоимость 1мматериала, из которого изготавливается дно бака, составляета стоимость 1мматериала, идущего на стенки бака,При каком отношении радиуса дня к высоте бака затраты на материал будут минимальными?

Ответ:

27) Сосуд с вертикальными стенками высотой наполненный невязкой жидкостью, стоит на горизонтальной плоскости. Определить местоположение отверстия, при котором дальность струи будет наибольшей, если скорость вытекающей жидкости по закону Торричелли равнагдерасстояние от отверстия до поверхности жидкости;ускорение свободного падения.

Ответ: на середине высоты

28) Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен 15 м. При каком радиусе полукруга окно будет пропускать наибольшее количество света?

Ответ: 2,1 м.

29) На странице книги печатный текст занимает площадь ширина верхнего и нижнего полей равнаа правого и левогоПри каком отношении ширина к высоте текста площадь всей страницы будет наименьшей?

Ответ:

30) Из круглого бревна, диаметр которого требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб? Сопротивление балки на изгибпропорционально произведению шириныее поперечного сечения и квадрата его высотыт.е.

Ответ:

4. Провести полное исследование указанных функций и построить их графики.

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

21) 22)

23) 24)

25) 26)

27) 28)

29) 30)

5. Провести полное исследование данных функций и построить их графики.

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

21) 22)

23) 24)

25) 26)

27) 28)

29) 30)

6. Найти наименьшее и наибольшее значения функции на отрезке

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

21) 22)

23) 24)

25) 26)

27) 28)

29) 30)

Решение типового варианта

Пример 1. Записать уравнение касательной к кривой в точке с абсциссой

Решение: Ордината точки касания

В любой точке В точке касанияПоэтому имеем уравнение касательной (по точкеи угловому коэффициенту):

.

Пример 2. По оси движутся две материальные точки, законы движения которых и(в метрах,в секундах). В какой момент времени их скорости окажутся равными?

Решение: Находим скорости обеих точек:

Так как то

Пример 3. От канала шириной 32 м отходит под прямым углом другой канал шириной 4 м. Определить наибольшую длину бревен, которые можно сплавлять по этой системе каналов. (Толщину бревна не учитывать)

Решение: Обозначим длину бревна через Тогда:

.

Рис.2

Исследуем функцию на экстремум:

.

Если , то. Так как, то из последнего уравнения имеем:. В окрестности этого значениязнак производнойопределяется знаком ее числителя, т.е. выражения. Имеем:

,

,

т.е.

.

Следовательно, при расстояниебудет минимальным, поэтому наибольшая длинабревна, сплавляемого из одного канала в другой, не может быть больше этого расстояния. Окончательно получаем:

м.

Пример 4. Провести полное исследование функции и построить ее график.

Решение: Исследуем данную функцию, придерживаясь в основном схемы, предложенной выше.

Областью определения функции является множество .

Ордината точки графика припри.

Точки пересечения графика данной функции с осями координат: и.

Легко находим, что – вертикальная асимптота, причем:

,

.

Находим наклонные асимптоты:

,

.

Таким образом, существует единственная наклонная асимптота .

Исследуем функцию на возрастание, убывание, локальный экстремум:

.

Из следует, откуда. В интервале, следовательно, функция возрастает в этом интервале; в, то есть функция убывает. Поэтому функция в точкеимеет локальный максимум:. В интервале, следовательно, функция убывает на этом интервале; в, то есть функция возрастает. В точкеимеет локальный минимум:.

Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем

.

Очевидно, что в интервале , и в этом интервале кривая выпуклая; в, то есть в этом интервале кривая вогнута. Так как при функция не определена, то точка перегиба отсутствует. График функции изображен на рис. 3

Рис.3

Пример 5. Провести полное исследование функции и построить ее график.

Решение: Воспользуемся общей схемой исследования функции. Область определения функции . Так какпри, то график проходит через начало координат. Функция принимает положительные значения в интервале. Вертикальных асимптот нет. Ищем наклонные асимптоты:

,

.

Получаем горизонтальную асимптоту . Так как, то функция нечетна и ее график симметричен относительно начала координат. Исследуем функцию на монотонность:

.

Если тооткудаЭти точки разбивают числовую ось на три интервала: ви функция в этом интервале убывает; в, и функция возрастает; ви функция в этом интервале убывает. В точкеимеем минимум:

а в точке максимум:

Исследуем свойства функции, связанные со второй производной:

Если то, откуда. В интервале, т.е. кривая выпукла в этом интервале; в, т.е. кривая вогнута; вкривая выпукла; вкривая вогнута. Так как в точкахвторая производнаяменяет знак, то при этих значенияхна графике

функции получаем точки перегиба, ординаты которых: . Полученные данные позволяют построить график функции.

Рис.4

Пример 6. Найти наименьшее и наибольшее значения функции на отрезке.

Решение: Находим критические точки:

,

если , то

.

Если , то; если же, то.

Из всех найденных критических точек только ипринадлежат отрезку. Вычислим значения данной функции при:

,

.

Следовательно, наибольшего значения на отрезке данная функция достигает в точке:, а наименьшего – в точкахи:.

112