
Домашнее задание к практическому занятию № 3.
1. Проверить совместность систем уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)

9)
 10)
10)

11)
 12)
12)

13)
 14)
14)

15)
 16)
16)

17)
 18)
18)

19)
 20)
20)

21)
 22)
22)

23)
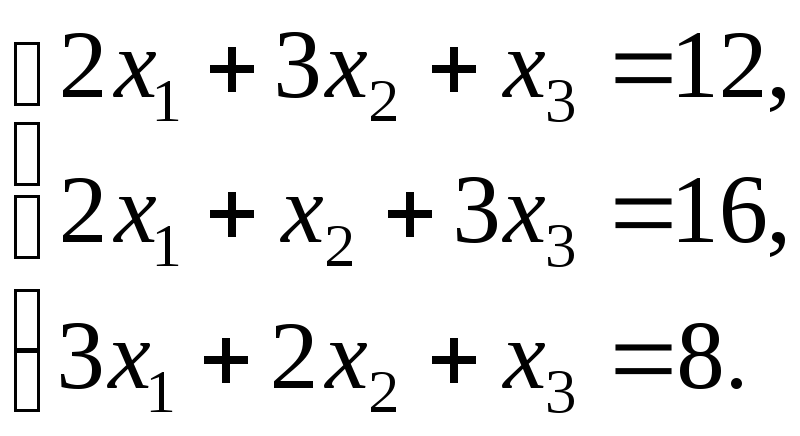 24)
24)

25)
 26)
26)

27)
 28)
28)

29)
 30)
30)

2. Проверить совместность систем уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)

9)
 10)
10)

11)
 12)
12)

13)
 14)
14)

15)
 16)
16)

17)
 18)
18)

19)
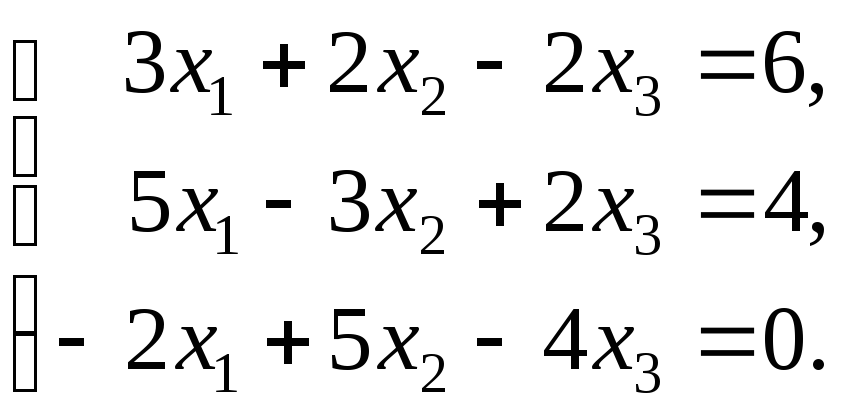 20)
20)

21)
 22)
22)

23)
 24)
24)

25)
 26)
26)

27)
 28)
28)

29)
 30)
30)

3. Решить однородную систему линейных алгебраических уравнений.
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)

9)
 10)
10)

11)
 12)
12)

13)
 14)
14)

15)
 16)
16)

17)
 18)
18)

19)
 20)
20)

21)
 22)
22)

23)
 24)
24)

25)
 26)
26)

27)
 28)
28)

29)
 30)
30)

4. Решить однородную систему линейных алгебраических уравнений.
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)

9)
 10)
10)

11)
 12)
12)

13)
 14)
14)

15)
 16)
16)

17)
 18)
18)

19)
 20)
20)

21)
 22)
22)

23)
 24)
24)

25)
 26)
26)

27)
 28)
28)

29)
 30)
30)

Решение типового варианта
Пример 1. Дана система линейных неоднородных алгебраических уравнений

Проверить, совместна ли эта система, и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
Решение: Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований найдем ранг матрицы

Данной системы и ранг расширенной матрицы

Для этого умножим
первую строку матрицы
![]() на
на
![]() и сложим со второй, затем умножим первую
строку на
и сложим со второй, затем умножим первую
строку на
![]() и сложим с третьей, поменяем местами
второй и третий столбцы. Получим
и сложим с третьей, поменяем местами
второй и третий столбцы. Получим

![]()

![]()
 .
.
Следовательно,
![]() (т.е числу неизвестных). Значит, исходная
система совместна и имеет единственное
решение.
(т.е числу неизвестных). Значит, исходная
система совместна и имеет единственное
решение.
а) по формулам Крамера
![]() ,
,
где




находим:
![]()
б) для нахождения
решения системы с помощью обратной
матрицы запишем систему уравнений в
матричной форме
![]() .
Решение системы в матричной форме имеет
вид
.
Решение системы в матричной форме имеет
вид
![]() .
Находим обратную матрицу
.
Находим обратную матрицу
![]() (она существует, так как
(она существует, так как
![]() ):
):
|
|
|
|
|
|
|
|
|
|
|
|

Решение системы:


Итак,
![]()
в) Решим систему
методом Гаусса. Исключим
![]() из второго и третьего уравнений. Для
этого первое уравнение умножим на 2 и
вычтем из второго, затем первое уравнение
умножим на 3 и вычтем из третьего:
из второго и третьего уравнений. Для
этого первое уравнение умножим на 2 и
вычтем из второго, затем первое уравнение
умножим на 3 и вычтем из третьего:

Из полученной
системы находим
![]() .
.
Пример 2. Дана система неоднородных алгебраических уравнений

Проверить, совместна ли эта система, и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера-Капелли. В расширенной матрице

меняем первый и третий столбцы местами, умножаем первую строку на 3 и прибавляем ко второй, умножаем первую строку на 2 и прибавляем к третьей, из второй строки вычитаем третью:

 .
.
Теперь ясно, что
![]() .
Согласно теореме Кронекера-Капелли, из
того, что
.
Согласно теореме Кронекера-Капелли, из
того, что
![]() ,
следует несовместность исходной системы.
,
следует несовместность исходной системы.
Пример 3. Решить однородную систему линейных алгебраических уравнений

Решение. Определитель системы
 ,
,
поэтому система
имеет единственное нулевое решение:
![]() .
.
Пример 4. Решить однородную систему линейных алгебраических уравнений

Так как
 ,
,
то система имеет
бесчисленное множество решений. Поскольку
![]() ,
возьмем любые два уравнения системы
(например, первое и второе) и найдем ее
решение.
,
возьмем любые два уравнения системы
(например, первое и второе) и найдем ее
решение.
Имеем:

Так как определитель
из коэффициентов при неизвестных
![]() и
и
![]() не равен нулю, то в качестве базисных
неизвестных возьмем
не равен нулю, то в качестве базисных
неизвестных возьмем
![]() и
и
![]() (хотя можно брать и другие пары неизвестных)
и переместим члены с
(хотя можно брать и другие пары неизвестных)
и переместим члены с
![]() в правые части уравнений:
в правые части уравнений:

Решаем последнюю систему по формулам Крамера :
![]() ,
,
где
![]() ;
;
![]() ;
;
![]() .
.
Отсюда находим,
что
![]() .
Полагая,
.
Полагая,
![]() ,
где
,
где
![]() произвольный коэффициент пропорциональности,
получаем решение исходной системы:
произвольный коэффициент пропорциональности,
получаем решение исходной системы:
![]() .
.
