
Домашнее задание к практическому занятию № 10.
1. Построить поверхности и определить их вид (название).
1) а)
![]() ; б)
; б)![]() .
.
2) а)
![]() ; б)
; б)![]() .
.
3) а)
![]() ; б)
; б)![]() .
.
4) а)
![]() ; б)
; б)![]() .
.
5) а)
![]() ; б)
; б)![]() .
.
6) а)
![]() ; б)
; б)![]() .
.
7) а)
![]() ; б)
; б)![]() .
.
8) а)
![]() ; б)
; б)![]() .
.
9) а)
![]() ; б)
; б)![]() .
.
10) а)
![]() ; б)
; б)![]() .
.
11) а)
![]() ; б)
; б)![]() .
.
12) а)
![]() ; б)
; б)![]() .
.
13) а)
![]() ; б)
; б)![]() .
.
14) а)
![]() ; б)
; б)![]() .
.
15) а)
![]() ; б)
; б)![]() .
.
16) а)
![]() ; б)
; б)![]() .
.
17) а)
![]() ; б)
; б)![]() .
.
18) а)
![]() ; б)
; б)![]() .
.
19) а)
![]() ; б)
; б)![]() .
.
20) а)
![]() ; б)
; б)![]() .
.
21) а)
![]() ; б)
; б)![]() .
.
22) а)
![]() ; б)
; б)![]() .
.
23) а)
![]() ; б)
; б)![]() .
.
24) а)
![]() ; б)
; б)![]() .
.
25) а)
![]() ; б)
; б)![]() .
.
26) а)
![]() ; б)
; б)![]() .
.
27) а)
![]() ; б)
; б)![]() .
.
28) а)
![]() ; б)
; б)![]() .
.
29) а)
![]() ; б)
; б)![]() .
.
30) а)
![]() ; б)
; б)![]() .
.
2. Записать уравнение и определить вид поверхности, полученной при вращении данной линии вокруг указанной оси координат, сделать рисунок.
1) а)
![]() ; б)
; б)![]() .
.
2) а)
![]() ; б)
; б)![]() .
.
3) а)
![]() ; б)
; б)![]() .
.
4) а)
![]() ; б)
; б)![]() .
.
5) а)
![]() ; б)
; б)![]() .
.
6) а)
![]() ; б)
; б)![]() .
.
7) а)
![]() ; б)
; б)![]() .
.
8) а)
![]() ; б)
; б)![]() .
.
9) а)
![]() ; б)
; б)![]() .
.
10) а)
![]() ; б)
; б)![]() .
.
11) а)
![]() ; б)
; б)![]() .
.
12) а)
![]() ; б)
; б)![]() .
.
13) а)
![]() ; б)
; б)![]() .
.
14) а)
![]() ; б)
; б)![]() .
.
15) а)
![]() ; б)
; б)![]() .
.
16) а)
![]() ; б)
; б)![]() .
.
17) а)
![]() ; б)
; б)![]() .
.
18) а)
![]() ; б)
; б)![]() .
.
19) а)
![]() ; б)
; б)![]() .
.
20) а)
![]() ; б)
; б)![]() .
.
21) а)
![]() ; б)
; б)![]() .
.
22) а)
![]() ; б)
; б)![]() .
.
23) а)
![]() ; б)
; б)![]() .
.
24) а)
![]() ; б)
; б)![]() .
.
25) а)
![]() ; б)
; б)![]() .
.
26) а)
![]() ; б)
; б)![]() .
.
27) а)
![]() ; б)
; б)![]() .
.
28) а)
![]() ; б)
; б)![]() .
.
29) а)
![]() ; б)
; б)![]() .
.
30) а)
![]() ; б)
; б)![]() .
.
3. Построить тело, ограниченное указанными поверхностями.
1) а)
![]() ;
;
б)
![]() .
.
2) а)
![]() ;
;
б)
![]() .
.
3) а)
![]() ;
;
б)
![]() .
.
4) а)
![]() ;
;
б)
![]() .
.
5) а)
![]() ;
;
б)
![]() .
.
6) а)
![]() ;
;
б)
![]() .
.
7) а)
![]() ;
;
б)
![]() .
.
8) а)
![]() ;
;
б)
![]() .
.
9) а)
![]() ;
;
б)
![]() .
.
10) а)
![]() ;
;
б)
![]() .
.
11) а)
![]() ;
;
б)
![]() .
.
12) а)
![]() ;
;
б)
![]() .
.
13) а)
![]() ;
;
б)
![]() .
.
14) а)
![]() ;
;
б)
![]() .
.
15) а)
![]() ;
;
б)
![]() .
.
16) а)
![]() ;
;
б)
![]() .
.
17) а)
![]() ;
;
б)
![]() .
.
18 а)
![]() ;
;
б)
![]() .
.
19) а)
![]() ;
;
б)
![]() .
.
20) а)
![]() ;
;
б)
![]() .
.
21) а)
![]() ;
;
б)
![]() .
.
22) а)
![]() ;
;
б)
![]() .
.
23) а)
![]() ;
;
б)
![]() .
.
24) а)
![]() ;
;
б)
![]() .
.
25) а)
![]() ;
;
б)
![]() .
.
26) а)
![]() ;
;
б)
![]() .
.
27) а)
![]() ;
;
б)
![]() .
.
28) а)
![]() ;
;
б)
![]() .
.
29) а)
![]() ;
;
б)
![]() .
.
30) а)
![]() ;
;
б)
![]() .
.
Решение типового варианта
Построить данные поверхности и определить их вид (название):
а)
![]() ;
б)
;
б)![]() .
.
а) Приведем уравнение к каноническому виду
![]() .
.
Получили уравнение
гиперболоида, расположенного так, как
показано на рис. 1; полуоси его «горлового»
эллипса
![]() ;
;
б) Приведем уравнение к каноническому виду
![]() .
.
Это уравнение
конуса второго порядка, ориентированного
указанным на рис.2. образом. Его сечения
плоскостями
![]() являются эллипсами.
являются эллипсами.
Записать уравнение поверхности, полученной при вращении:
параболы
 :
а) вокруг оси
:
а) вокруг оси ;
б) вокруг оси
;
б) вокруг оси ;
;эллипса
 :
а) вокруг оси
:
а) вокруг оси ;
б) вокруг оси
;
б) вокруг оси ;
;
1. В соответствии с общим правилом (11) получения уравнения поверхности вращения находим:
а)
![]()
(алгебраическая поверхность четвертого порядка (рис. 3));
б)
![]()
(параболоид вращения (рис. 4)).
Имеем:
а)
![]() .
.
Получили сплюснутый
вдоль оси
![]() эллипсоид вращения (сфероид), полуоси
его главных сечений
эллипсоид вращения (сфероид), полуоси
его главных сечений![]() (рис.5);
(рис.5);
б)
![]() .
.
(вытянутый вдоль
оси
![]() эллипсоид вращения (рис. 5):
эллипсоид вращения (рис. 5):![]() .
.
Построить тело, ограниченное данными поверхностями:
а)
![]() ;
;
б)
![]() .
.
|
Рис.1 |
Рис.2 |
|
Рис.3 |
Рис.4 |
|
Рис.5 |
Рис.6 |
|
Рис.7 |
|
а) Построение
выполнено на рис. 7:
![]() –
дуга параболы, являющейся пересечением
гиперболического параболоида
–
дуга параболы, являющейся пересечением
гиперболического параболоида![]() с плоскостью
с плоскостью![]() ;
;![]() – пересечение поверхности
– пересечение поверхности![]() с плоскостью
с плоскостью![]() – характерные точки тела;
– характерные точки тела;
б) Построение
выполнено на рис.8:
![]() – дуга параболы, являющейся пересечением
параболического цилиндра с плоскостью
– дуга параболы, являющейся пересечением
параболического цилиндра с плоскостью![]() – характерные точки тела.
– характерные точки тела.







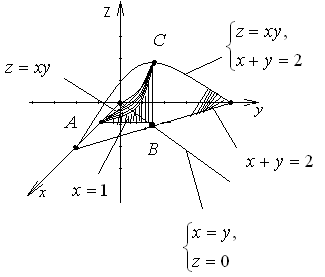
 Рис.8
Рис.8