Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Черчение / т 2.ppt
X
- •Тема 2 Плоскости и их проекции
- •1.Типы задач начертательной геометрии
- •ТИПЫ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ
- •Расстояние от точки А до горизонтально
- •Расстояние от точки до фронтали z
- •Определить натуральную величину отрезка
- •СПОСОБЫ ГРАФИЧЕСКОГО ЗАДАНИЯ ПЛОСКОСТЕЙ И ИХ КЛАССИФИКАЦИЯ
- •плоскость общего
- •Плоскости параллельные плоскостям проекций – занимают частное положение в
- •горизонтально
- •фронтально
- •профильно
- •Плоскости параллельные плоскостям
- •Фронтальная плоскость
- •Профильная плоскость
- •Взаимное
- •Определение взаимного положения прямой и
- •Возможны три случая относительного расположения прямой и плоскости:
- •Прямая принадлежит плоскости, если
- •Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо
- •Главные линии плоскости
- •плоскость общего положения –
- •плоскость общего положения – фронталь
- •плоскость общего положения -
- •она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой
- •Прямая линия перпендикулярная
- •Для нахождения точки пересечения прямой с
- •Линия пересечения прямой и
- •Взаимное
- •Плоскости параллельны, если две
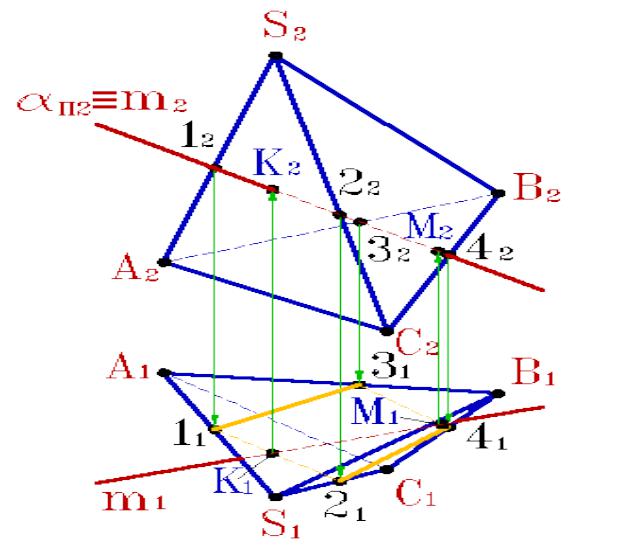
- •Пересечение плоскости общего положения заданной
- •Заключение
- •Многогранники
- •Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники
- •Призма - многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с
- •Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют
- •Гексаэдр - правильный шестигранник
- •Октаэдр - правильный восьмигранник
- •Додекаэдр - правильный
- •Икосаэдр - состоит из 20 равносторонних и равных
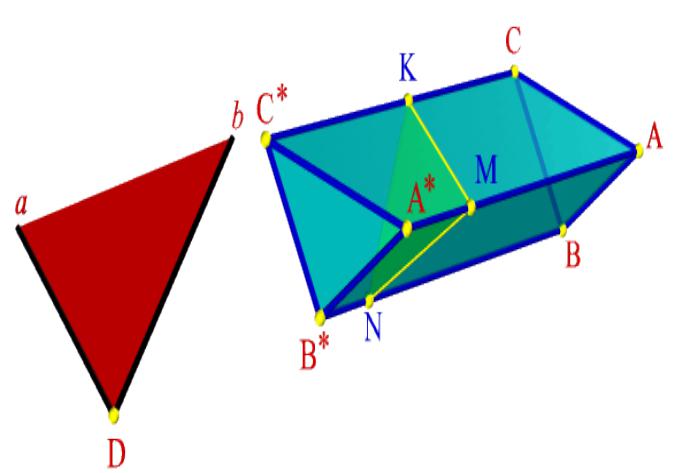
- •Построение сечения многогранника требует многократного решения задачи о нахождении точки пересечении прямой с
- •Для определения точек пересечения
- •Взаимное пересечение многогранников
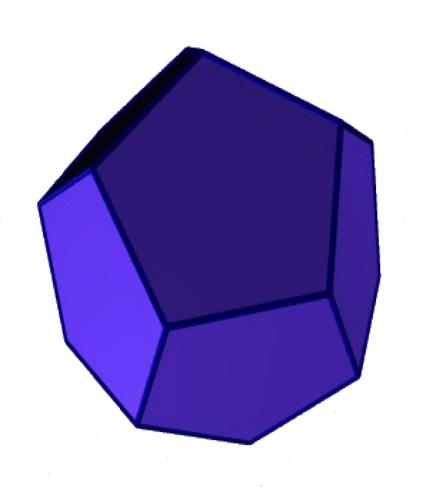
Додекаэдр - правильный
двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины

Икосаэдр - состоит из 20 равносторонних и равных
треугольников, соединенных по пять около каждой вершины
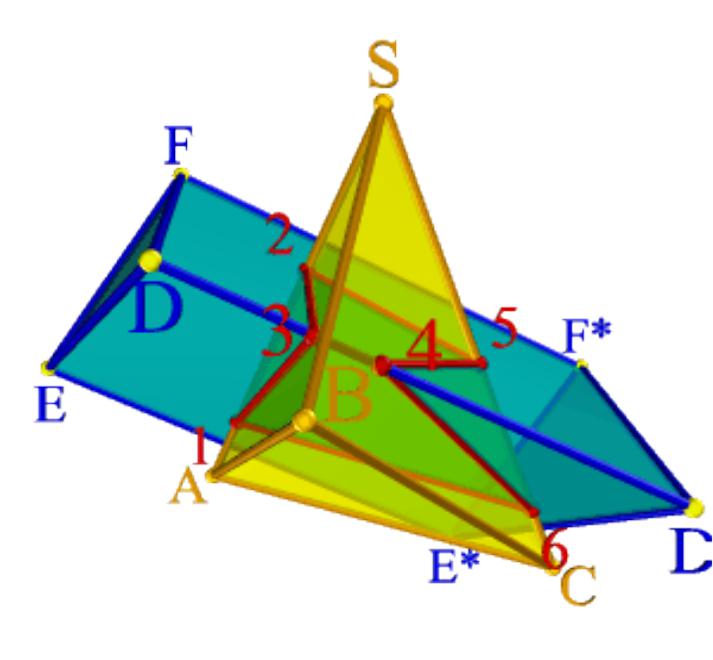
Построение сечения многогранника требует многократного решения задачи о нахождении точки пересечении прямой с плоскостью. Точки, в которых ребра многогранника пересекаются с заданной плоскостью, будут вершинами искомого сечения.
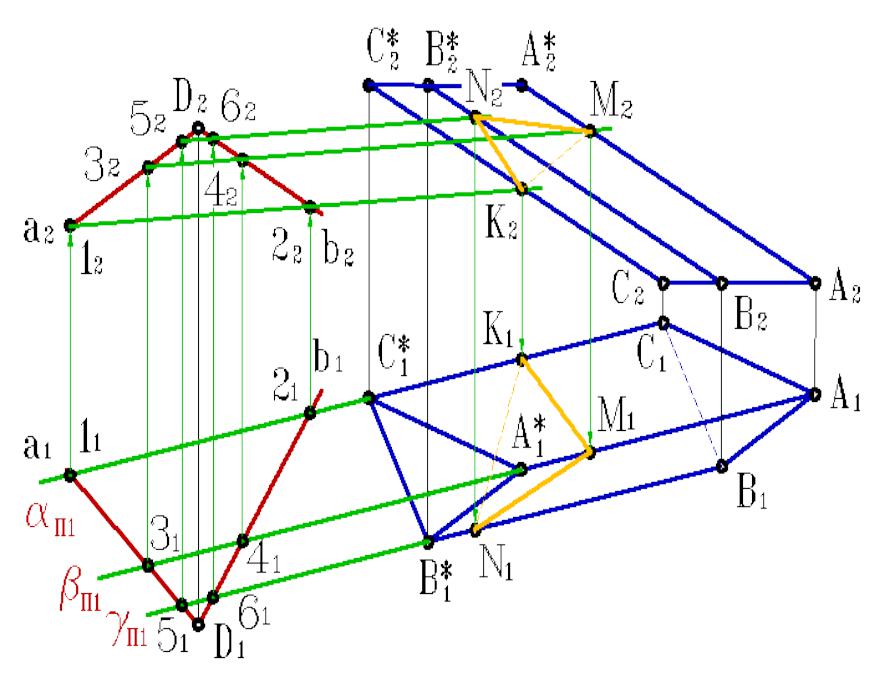
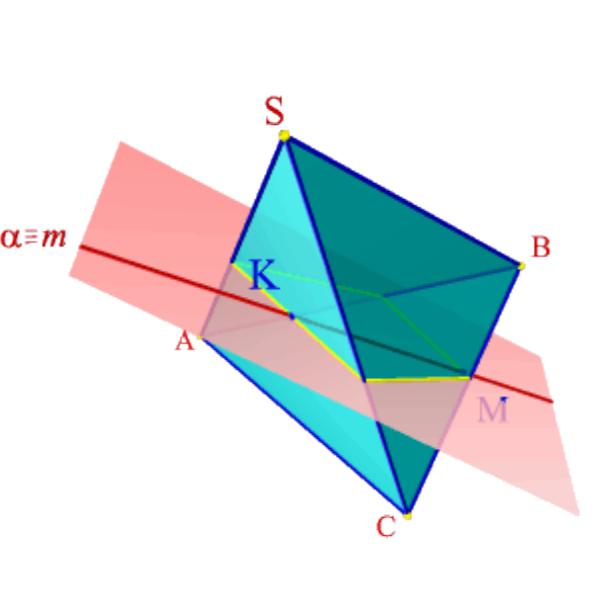
Для определения точек пересечения
прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с плоскостями граней