Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Черчение / т 3.ppt
Прямая линия перпендикулярная |
|||
плоскости |
B2 |
|
f2 |
D2 |
|
||
А2 |
|
|
h2 |
|
|
|
С2 |
D1 |
|
С1 |
h |
|
|
1 |
|
|
|
|
f1 |
А1 |
|
B1 |
|
Линия пересечения прямой и
Bплоскости
2 n2
А2 |
|
|
K2 |
С2 |
11=2 |
|
|||
|
С1f |
|||
1 |
2 |
n1 |
||
|
1 |
|
|
|
|
|
|
|
|
А1 |
11 |
K1 |
B |
|
|
|
|
|
1 |
|
|
|
|
1 |
Для определения точек пересечения
прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с плоскостями граней
Взаимное пересечение многогранников
Теорема о проецировании прямого угл
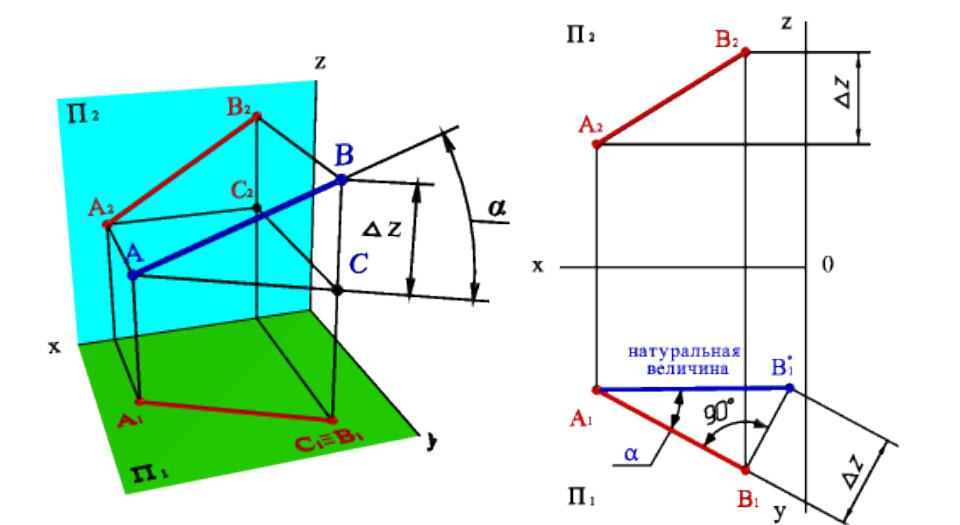
Определение длины отрезка прямой, линии углов наклона прямой к плоскостям проекций
А2
x12 |
B2 П2 |
|
П1 |
||
B1 |
||
А1 |
П4 |
|
B4 |
x14 А4