Примеры решения задач

Задача 3.1. Электрон находится в одномерном бесконечно глубоком потенциальном ящике шириной l. Определить наименьшую разность двух соседних энергетических уровней (в эВ) электрона в двух случаях: 1) l=10 см; 2) l=1 нм. Сравнить полученные результаты. Показать на графике распределение плотности вероятности обнаружения электрона на данном уровне.

Решение.

Из формулы (3.3) для собственных значений энергии электрона при его движении в потенциальном ящике следует, что отношение энергии равно E₁: E₂: E₃:…=1:4:9: …, поэтому наименьшая разность уровней

1) (Дж) = 1,1·10^-16 эВ.

2) (Дж) = 1,1 эВ.

Как видно из полученных результатов, в первом случае разность уровней столь мала, что дискретностью энергии можно пренебречь и считать, что в случае, когда электрон движется в ящике, размер которого много больше атомных размеров (~10^-10 м), его энергия изменяется непрерывно. Во втором случае электрон движется в потенциальном ящике, размер которого соизмерим с размерами атома. Значение ΔE получилось достаточно большим и дискретностью изменения энергии электрона пренебречь нельзя.

Ответ: 1) 1,1·10^-16 эВ; 2) (Дж) = 1,1эВ.

Задача 3.2. Электрон находится в бесконечно глубоком одномерном прямоугольном ящике шириной l. Определить: 1) вероятность того, что электрон находящийся в первом возбужденном состоянии, будет обнаружен в крайней левой четверти ящика; 2) вероятность нахождения электрона в середине ящика.

Решение.

Вероятность нахождения частицы в бесконечно узком интервале dx определяется формулой (3.4), следовательно, вероятность обнаружения частицы в левой четверти ящика, т.е. в интервале , равна.

Учитывая соотношение (3.2) и то, что первому возбужденному состоянию соответствует главное квантовое число n=2, получим

.

Произведя замену и, разбив интеграл на два, перейдем к выражению

,

.

Нетрудно показать, что вероятность обнаружения электрона в правой крайней четверти ящика тоже равна 0,5.

Д

Рис. 3.1

ля ответа на второй вопрос достаточно определить плотность вероятности обнаружения частицы в точке

.

Распределение плотности вероятности обнаружения электрона на втором уровне приведено на рис. 3.1.

Задача 3.3. Электрон с энергией 3,6 эВ движется в положительном направлении оси x, встречая на своем пути потенциальный барьер. Чему равна высота барьера (в эВ), если вероятность прохождения через него электрона равна 0,2, а ширина барьера 0,5 нм?

Решение.

Вероятность W прохождения частицы сквозь потенциальный барьер по физическому смыслу совпадает с коэффициентом прозрачности D, поэтому может быть определена по формуле (3.5)

,

где U – искомая высота потенциального барьера.

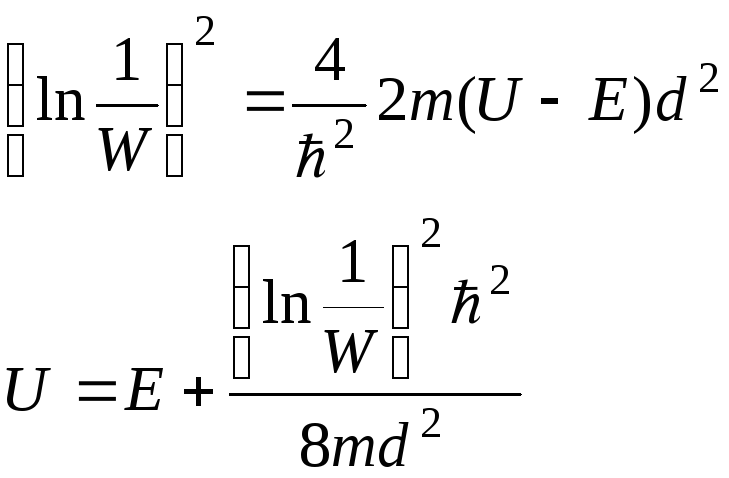
(эВ).

Ответ: U=3,6 эВ.

Задача 3.4. Определить возможные значения орбитального момента импульса электрона в возбужденном атоме водорода, если энергия возбуждения 12,09 эВ.

Решение.

Орбитальный момент импульса электрона определяется квантовым числом ℓ по формуле (3.7). Так как ряд возможных значений ℓ ограничен величиной (n-1), найдем главное квантовое число n с помощью формулы

E =hν=E_n-E₁; E =hcR.

Учитывая, что hcR= E _i=13,6 эВ, получим 12,09=13,6, откудаиn=3, следовательно, ℓ=0, 1, 2.

Используя формулу (3.7), получим:

при ℓ=0 L_ℓ=0;

при ℓ=1 L_ℓ==1,49·10^-34 Дж·с;

при ℓ=2 L_ℓ==2,6·10^-34 Дж·с.

Ответ: 0; 1,49·10^-34 Дж·с; 2,6·10^-34 Дж·с.

Задача 3.5. Определить наименьший угол, который может образовать вектор орбитального момента импульса электрона в атоме с направлением внешнего магнитного поля. Электрон в атоме находится в d-состоянии.

Решение.

d-состоянию электрона соответствует значение орбитального квантового числа ℓ=2, следовательно, магнитное квантовое число m_ℓ, определяющее проекцию орбитального момента импульса электрона на направление магнитного поля, может принимать значения: -2, -1, 0, +1, +2.

Орбитальный момент импульса равен (3.7)

.

Этот вектор занимает в магнитном поле такое положение, что его проекции на направление этого поля равны (3.8):

L_H = –2ħ, –1ħ, 0, +1ħ, +2ħ.

На рис. 3.2 представлены возможные ориентации вектора орбитального момента импульса электрона во внешнем магнитном поле. Из рисунка видно, что для наименьшего угла α

α=35˚10′.

Ответ: α=35˚10′.

4. Строение ядра. Энергия связи. Радиоактивность

Основные формулы:

Ядро обозначается тем же символом, что и нейтральный атом: , гдеZ – зарядовое число, определяющее число протонов в ядре, A – массовое число, определяющее число нуклонов (протонов и нейтронов) в ядре.

Закон радиоактивного распада

N=N₀exp(-λt), (4.1)

где N₀ – число ядер в начальный момент времени (t=0), N – число ядер в момент времени t, λ – постоянная радиоактивного распада.

Количество атомов, распавшихся за время t

(4.2)

Период полураспада T – промежуток времени, за который число ядер уменьшается в два раза. Период полураспада и постоянная распада связаны соотношением

(4.3)

Если подставить (4.3) в соотношение (4.1), закон радиоактивного распада можно представить в другом виде

(4.4)

В случае, когда промежуток времени Δt мал по сравнению с периодом полураспада Т (Δt<<T), то число распавшихся ядер можно определять по приближенной формуле

ΔN ≈ λ·N·Δt (4.5)

Среднее время жизни τ радиоактивного изотопа – промежуток времени, за который число ядер уменьшается в e раз

(4.6)

Активность радиоактивного изотопа – число ядер, распавшихся в единицу времени

(4.7)

начальная активность (при t=0)

A₀=λN₀ (4.8)

Активность изменяется с течением времени по закону

(4.9)

Уравнения α- и β- распадов (правила смещения):

(4.10)

(4.11)

Закон поглощения γ-излучения веществом

I=I₀e^–μx, (4.12)

где I₀ – интенсивность γ-излучения, падающая на слой вещества толщиной x, I - интенсивность γ-лучей, прошедших слой x, μ – линейный коэффициент поглощения.

Энергия ядерной реакции (или тепловой эффект реакции)

, (4.13)

где и - суммы масс покоя частиц, соответственно, до и после реакции,с – скорость света в вакууме. Если >0, тореакция идет с выделением энергии; если <0, тореакция идет с поглощением энергии.

Энергетический выход ядерной реакции чаще измеряют не в системе СИ (Дж), а в МэВ.

В этом случае массу частиц измеряют в атомных единицах массы (а.е.м.), а значение .

Все ядерные реакции идут в соответствии с законами сохранения заряда, массового числа (число нуклонов), полной энергии и импульса.

Под полной энергией подразумевается полная релятивистская энергия, определяемая по формуле

, (4.14)

где - сумма энергий покоя частиц до реакции,- сумма их кинетических энергий. Справа стоят те же физические величины, относящиеся к частицам, образующимся в результате реакции.

Энергия связи ядра, т.е. энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его частицы без сообщения им кинетической энергии, определяется формулой

(4.15)

где m_p, m_n и m_я , соответственно, массы протона, нейтрона и ядра.

Так как в справочных таблицах приводятся значения масс атомов, а не ядер, надо перейти к соотношению, содержащему эти величины. Масса ядра m_я= m_а-Zm_e, где m_e – масса электрона, тогда

Учитывая, что - масса атома водорода, можно записать

(4.16)