1.2 Эффект Фарадея. Феноменологическое рассмотрение.

Магнитное вращение плоскости поляризации линейно поляризованного излучения (эффект Фарадея) было обнаружено Фарадеем в 1845г. Это был первый эксперимент, в котором обнаружилась связь между оптическими и магнитными явлениями.

Фарадеевское вращение начало широко применяться для определения параметров энергетической структуры после работы Митчелла, в которой было предложено находить величину эффективной массы из исследования эффекта Фарадея в ИК области спектра. В настоящее время практически все наиболее достоверные значения эффективных масс m при T≥77K в большинстве исследованных полупроводников получены из изучения эффекта Фарадея на свободных носителях. Исследования эффекта Фарадея при ћω~E_g в области низких температур и сильных магнитных полей позволяют определить значения g-факторов.

Эффект Фарадея заключается во вращении плоскости поляризации линейно поляризованного излучения при его распространении через вещество, находящееся в магнитном поле, параллельном направлению распространения излучения. Схема, иллюстрирующая фарадеевское вращение в полупроводнике, показана на рис.1.

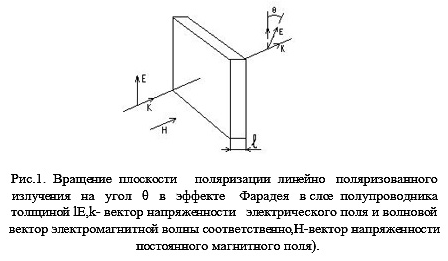
Знак эффекта Фарадея определяется только направлением магнитного поля, т.е. вращение происходит в одну и ту же сторону по отношению к наблюдателю, вне зависимости от того, распространяется ли излучение вдоль магнитного поля или против него. Вращение считается положительным, если плоскость поляризации поворачивается вправо по отношению к наблюдателю, смотрящему вдоль магнитного поля. На рис.6 поворот плоскости поляризации в эффекте Фарадея соответствует положительному углу вращения θ. Величина угла θ пропорциональна первой степени магнитного поля.

Независимость знака магнитного вращения плоскости поляризации от направления распространения излучения следует из симметрии поля (группа ∞/m). Применение операции симметрии – отражения в плоскости, перпендикулярной направлению магнитного поля,- не приводит к изменению знака θ. Это отличает магнитное вращение от естественного, происходящего в оптически активных средах, которые являются подгруппами симметрии группы ∞/2. В последнем случае поворот вокруг оси второго порядка, приводит к изменению направления естественного вращения плоскости поляризации на обратное.

Феноменологическое рассмотрение магнитного вращения плоскости поляризации света основано на представлениях о различии характеристик среды для двух неодинаковым образом поляризованных компонент излучения.

Пусть линейно поляризованная электромагнитная волна нормально падает на слой вещества. Линейное колебание вектора E волны можно представить как суперпозицию циркулярно право- и лево- поляризованных компонент, угловые скорости вращения которых одинаковы. При включении магнитного поля для право- и лево- поляризованных компонент возникают неодинаковые условия для распространения. Частоты вращения электрических векторов двух компонентов в системе координат, связанной с вращающимся электроном, отличаются для связанного электрона, находящегося в центральном поле сил атома, от частоты волны ω на ларморовскую частоту ±ω_L=. Вследствие этого показатель преломления, являющийся функцией частоты, будет различным для право- и лево- поляризованных компонент, и эти компоненты будут распространяться с различной скоростью.

Экспериментально различная скорость распространения циркулярно право- и лево- поляризованных пучков света в слое вещества, помещенного в магнитное поле, была показана Риги и Беккерелем по смещению интерференционных полос. Смещение возникало при включении магнитного поля, что говорит о разной скорости распространения через кристалл, помещенный в магнитное поле двух поляризованных по кругу в разные стороны пучков света.

Прямое доказательство разложения линейно поляризованного излучения, падающего на магнитоактивный кристалл, на две циркулярно поляризованные в разные стороны компоненты было осуществлено Брейсом, который в качестве диспергирующего элемента использовал призму специальной конструкции. Так как право- и лево- поляризованные компоненты имеют разные скорости распространения, то на выходе из призмы, помещенной в магнитное поле они должны отклоняться на разные углы. Угол развода этих лучей, однако, чрезвычайно мал, так как показатели преломления для двух циркулярно поляризованных в разные стороны компонент в обычных полях напряженностью порядка 10⁴ Э различаются между собой на величину порядка 10^-5. Для увеличения угла развода компонент Брейс использовал специальную конструкцию двух призм, разделенных пластинкой в полволны. После двадцатикратного прохождения через такую конструкцию первоначально линейно поляризованного излучения удалось геометрически разделить право- и лево- поляризованные компоненты.

Рассмотрим процесс распространения линейно поляризованного излучения, распространяющегося вдоль направления магнитного поля, через слой вещества, поворачивающего плоскость поляризации на некоторый угол θ (магнитоактивная среда).

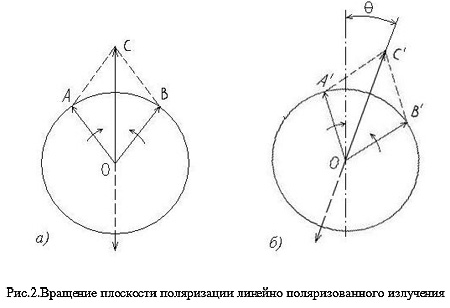
До вступления в магнитооптически активную среду (рис 2,а) векторы ОА и ОВ, изображающие электрические векторы двух циркулярно поляризованных в разные стороны компонент излучения, вращаются в разные стороны с одинаковой угловой скоростью. Результирующим вектором двух циркулярных компонент является вектор ОС, сохраняющий свое направление в пространстве и представляющий собой линейно поляризованное излучение. При распространении излучения по магнитооптически активному кристаллу показатели преломления для право- и лево- поляризованного излучения получаются разными, поэтому компоненты распространяются с различными скоростями. Вследствие этого, если при вступлении в среду компоненты имели одинаковую фазу, при выходе из нее они приобретут некоторую разность фаз. Схема, иллюстрирующая положение циркулярно поляризованных компонент на выходе из среды, показана на рис. 2,б. Векторы ОА' и ОВ' также вращаются в разные стороны с одинаковой угловой скоростью, но теперь их результирующий электрический вектор ОС' колеблется в плоскости, составляющей угол θ с его первоначальным положением до входа в среду. При совпадении направления ОА' с первоначальным положением результирующего вектора ОС видно, что разность фаз между компонентами ОА' и ОВ' равна 2θ, т.е. угол поворота плоскости поляризации в эффекте Фарадея равен половине разности фаз между двумя циркулярно поляризованными в разные стороны компонентами излучения.

Угол поворота плоскости поляризации можно выразить через значения показателей преломления n_-=n(ω+ω_L) и n₊=n(ω-ω_L) для двух компонент, поляризованных по кругу. Число оборотов вектора индукции для правополяризованной по кругу компоненты на единице длины будет 1/λ₊, а для левополяризованной – 1/λ_-, где

λ_+,-=(2)

ω – частота излучения, с – скорость света в вакууме. Разность числа оборотов этих компонент и определит разность фаз на длине l. Таким образом, для угла вращения плоскости поляризации получаем выражение

θ===[рад] (3)

Видно, что плоскость поляризации поворачивается в сторону вращения той циркулярно поляризованной компоненты, скорость распространения которой больше.

Полученное для θ выражение обусловлено разностью фаз, возникающей при прохождении компонент, поляризованных по правому и левому кругам, через объем кристалла. Однако кроме объемного вращения плоскости в некоторых случаях становится существенным вращение на границе раздела двух сред (θ_пов), а также вращение, связанное с интерференцией волны внутри тонких слоев исследуемого материала (θ_инт). И в общем случае величина определяется тремя слагаемыми:

θ=θ_об+θ_пов+θ_инт(4)

В спектральном диапазоне λ≤50 мкм, в котором обычно проводятся исследования ИК фарадеевского вращения:

θ==, (5)

Из этого выражения видно подобие спектральной зависимости θ(ω) спектрам отражения или пропускания методов модуляционной спектроскопии, позволяющих получить информацию о зонном спектре полупроводников вблизи критических точек для изучения особенностей спектров отражения или пропускания, маскирующихся на фоне сплошного отражения (пропускания). В методах модуляционной спектроскопии величина измеряемого сигнала также связана с производной диэлектрической проницаемости по частоте излучения или другому параметру.

Поворот плоскости поляризации в магнитном поле можно выразить через так называемую постоянную Верде V, которая входит в эмпирический закон:

θ =VHl. (6)

Значение постоянной Верде для различных полупроводниковых материалов колеблется в широких пределах (V~(10^-3-10^-7)) в зависимости от величины эффективной массы и концентрации носителей, g-факторов, длины волны излучения, температуры. В полупроводниках при частотах излучения ω, далеких от характеристических частот ω_с, ν=1/τ, где ω_с – частота циклотронного резонанса, в магнитных полях напряженностью Н≤10⁵Э обычно V не зависит от величины Н.