Расчет комплексного сопротивления шины

Параметры шины в синусоидальном режиме определяем вновь с помощью теоремы Умова-Пойнтинга . (5.138)

Учитывая, что электромагнитная энергия поступает в шину из окружающего пространства только через ее боковые поверхности' а также обозначенные на рис. 137 направления векторов и на этих поверхностях, из (5.138) получим

. (5.139)

Подготовим данные для подстановки в (5.139). Из (5.135) и (5.136) при z = 0

, (5.140)

. (5.141)

Из (5.135) и (5.136) при z = a (5.142)

,

. (5.143)

Подстановка (5.140)—(5.143) в (5.139) позволяет подучить выра­жение для внутреннего сопротивления шины А:

. (5.144)

С учётом того, что (5.145)

окончательно для комплексного сопротивления средней шины имеем

. (5.146)

Как и ранее, интерес представляют два крайних режима, когда ра→0 и ра≥2.

В первом случае шина является прозрачной для электромагнитной волны, ток в ней распределяется равномерно и из (5.146) при shра ≈ ра, chpa ≈ 1, как и на постоянном токе,

. (5.147)

Во втором случае ярко проявляются поверхностный эффект и эффект близости. При больших значениях аргумента (pa) shpa →∞, cthpa ≈ 1 и, следовательно, из (5.146)

. (5.148)

Сопоставляя (5.148) и (5.125), нетрудно видеть, что в трехфаз­ном шинопроводе при ярко выраженном поверхностном эффекте сопротивление центральной шины вдвое превышает сопротивления крайних шин. В связи с этим для обеспечения в целом однороднос­ти параметров трехфазного шинопровода необходима соответству­ющая транспозиция шин на отдельных участках линии. Если же сравнить это сопротивление с сопротивлением уединенной шины, то окажется, что проявление эффекта близости увеличивает его в трехфазной системе в 4 раза. Интересно отметить, что при огово­ренных условиях (ра≥2) из (5.21) и (5.22) следует, что на левой и правой поверхностях шины плотности тока соответственно равны , т.е. их начальные фазыотличаются на угол 2π/3. Это важное обстоятельство свидетельствует о том, что мгновенные значения токов в одной и той же шине име­ют в течение двух третей периода противоположные направления.

Эквивалентные схемы замещения трехфазного шинопровода при симметричной системе токов

При расчетах систем с трехфазными шинопроводами необходи­мо учитывать, что электромагнитные поля существуют не только внутри самих шин, но и в пространствах между ними. Эти внут­ренние и внешние поля связаны уравнениями Максвелла—Фара-дея и обуславливают единый процесс передачи энергии от источ­ника к нагрузке.

Выше было показано, что граничные условия для расчета по­лей в шинах определяются с помощью метода наложения. Они за­висят от токов в шинах, а следовательно, и внутренние комплексные сопротивления шин становятся зависящими от режи­ма работы всей трехфазной цепи. Помимо этого и внешние маг­нитные потоки, сцепленные с шинами, являются функциями то­ков в шинах, а это значит, что и напряжения электромагнитной индукции напрямую зависят и от режима работы линии и расстоя­ния между шинами. Поэтому, исходя из методологических соображения, здесь будет рассмотрен простейший случай, когда трехфаз­ная линия запитана симметричной системой токов и замкнута на­коротко в конце. При такой постановке, естественно, оказывается несимметричной система линейных и фазных напряжений в линии.

На рис. 34 изображены две проекции трехфазной линии. На нем указаны геометрические размеры шинопровода, условно-поло­жительные направления векторов поля , а также электричес­ких токов линейных напряжений и магнитных потоков в пространствах между шинами и в шинеА —

Рис.34

Токи фаз формируют систему прямой последовательности ,

С помощью закона электромагнитной индукции или второго урав­нения Максвелла в интегральной форме для данной системы пред­ставляется возможным составить три контурных уравнения типа

Здесь магнитный поток пронизывает поверхность, опирающу­юся на замкнутый контурl. Как следует из рис. 34, контур СА (ле­вая сторона шины А, внутренняя сторона шины С и напряжение ,) сцеплен с потокоми, следовательно, для него имеем

. (5.149)

Аналогично для контура А В

(5.150)

и внесшего контура ВС, сцепленного с потоками ,

(5-151)

В связи с тем, что в шинах В и С расчет поля осуществляется при таких же граничных условиях, как и в двухпроводной линии из (5.149)—(5.151) имеем:

, (5.152)

. (5.153)

Учитывая, что в пространстве между шинами Л, С и А, В найдем, что

(5.154)

(5.155)

Магнитный поток в шине А определим путем интегрирования (5.136) по сечению шины:

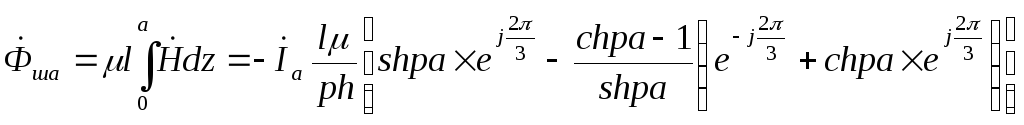, (5.156)

или после несложных преобразований

(5.156)

Из приведенных решений (5.135), (5.136) для шины А имеем

. (5.157)

. (5.158)

И, наконец, внутреннее сопротивление шины А

. (5.159)

Делаем подстановку (5.152), (5.155), (5.157) в (5.149)

. (5.160)

Добавим в (5.160) два равных по величине и противоположных по знаку слагаемых

Тогда после преобразований

или, учитывая, что , для линейного напряжения получим:

(5.161)

Раскроем далее уравнение для контура, образованного шинами A и B. Для этого подставим (5.153), (5.155), (5.158) в уравнение (5.150):

. (5.162)

Добавим, как и ранее, в (5.160) два слагаемых

.

После приведения подобных с учетом (5.159) имеем

,

а так как , то окончательно для линейного напря­жения получим

. (5.163)

Введем обозначение . (5.164)

Тогда контурные уравнения (5.162) и (5.163) примут вид

, (5.165)

. (5.166)

Легко видеть, что полученным уравнениям соответствует следующая эквивалентная схема с сосредоточенными параметрами (рис. 35)

_;27Г

1

Рис. 35 Рис.36

Так как для цепи с тремя ветвями можно со­ставить лишь два независи­мых контурных уравнения, то уравнение (5.151) для контура В, С должно яв­ляться следствием двух первых (5.149) и (5.150). В связи с этим по уравне­нию (5.151) можно прове­рить правильность решения задачи в целом. Так, делая подстановку (5.152), (5.153)—(5,151) в (5.132) и учитывая (5.164), находим

. (5.167)

Это же уравнение является и линейной комбинацией (5.165) и (5.166) или контурным уравнением для схемы на рис. 36.

С помощью тео­ремы о компенса­ции в полученную схему замещения (рис. 35) введем вместо сопротивле­ния Z_A эквивалент­ную ЭДС: E_A = I_AZ_A. Если далее осуще­ствить вынос ЭДС (Е_А) за узел и разделить цепь на от­дельные ветви, то после несложных преобразований можно получить схему замеще­ния для каждой фазы отдельно (рис. 37).

Рис. 37

Полученные уравнения и схема замещения трехфазного шинопровода позволяют сделать следующие выводы:

1. При симметричной системе токов в общем случае параметры всех трех фаз отличаются друг от друга даже при одинаковых раз­мерах шин и расстояниях между ними, так как в фазы В и С сопро­тивление Z_M входит с разными знаками.

2. Сопротивления Z_M вносятся лишь в крайние шины и если при этом ток в крайней шине опережает по фазе на угол 2π/3 ток цен­тральной шины, то сопротивление Z_M вносится в эту шину со зна­ком плюс, и если отстает, то со знаком минус.

3. Для прозрачных шин, когда поверхностный эффект практи­чески не проявляется, вносимые сопротивления Z_M no величине близки к нулю.

4.При постановке исходной задачи предполагалось, что в соот­ветствии с рис. 32 толщина шин (а) и расстояния между шинами (b) одинаковы. Однако полученные результаты в виде уравнений(5,165), (5.166) и схема замещения (рис. 35) позволяют значитель­но расширить область их практического использования. В частности, могут быть решены задачи о расчете параметров трехфазных шинопроводов, когда шины имеют разные толщины и физические свой­ства (γ), а также различные расстояния между собой.