Комплексное сопротивление шины при наличии эффекта близости

Для расчета сопротивления шины при наличии эффекта близо­сти вновь воспользуемся теоремой Пойнтинга, которая позволяет определить Z_шины

В качестве замкнутой поверхности выберем поверхность шины на длине l и разобьем эту поверхность на составляющие (рис. 27) Sзамкн ⁼ S₁+S₂+S_3,4+2S_4T. Определим значения потоков вектора для каждой из этих поверхностей.

Рис.27

С учетом, что атоП=П_z. Как видно, на всех поверхностях, за исключением S₁ и S₂, векторы и перпендикулярны и, следовательно, через эти по­верхности поток вектора Пой­нтинга отсутствует. К тому же, если обратиться к (5.114), то приz = О H(0) = 0. Если это так, то и .

Таким образом, полный поток вектора определяется лишь потоком через поверх-ностьS₁. При этом паралле­лен (направление векторов одинаково) и всюду на S₁, мо­дуль вектора =const. В итоге

.

Раскроем это выражение, для чего (5.ИЗ) и (5.114) перепишем при z=a:

, (5.115)

(5.116)

и, следовательно,

. (5.117)

Отметим, что сопротивление Z определено по результатам ис­следования электромагнитного поля только внутри шины и поэто­му его называют внутренним Z = Z_вн = R_вн +jx_вн.

Преобразуем (5.117), учитывая, что р²=jωμγ. Тогда выражение для комплексного внутреннего сопротивления шины будет иметь вид

. (5.118)

Если сопоставить выражения (5.117) и (5.115) соответственно для внутреннего сопротивления шины и вектора электрической на­пряженности на ее поверхности z = а, то нетрудно установить, что

, (5.119)

где Z_вн.о. — удельное (на единицу длины) внутреннее сопротивле­ние шины.

Как и ранее, интерес представляют два крайних случая, когда

1. ра « 1 (поверхностный эффект не проявляется);

2. ра≥2 (случай ярко выраженного поверхностного эффекта).

В первом случае первое слагаемое при разложении функции в степенной ряд cthpa ≈ l/pa и, следова­тельно, для прозрачной шины, как и на постоянном токе

.

Если pa≥2, то cthpa≈1, a

.

Очевидно, что в данном случае R*_~=lp/h∆ т.е. активное сопротивление шины при ярко выраженном эффекте оказывается обратно пропорциональным глубине проникновения ∆ (рис. 28).

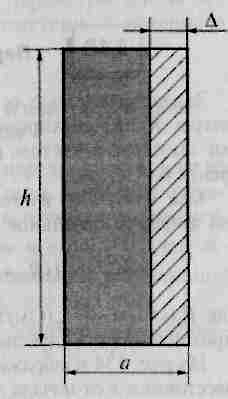
Рис. 28

Важно отметить, что в случае проявле­ния эффекта близости ток в шине про­текает уже не в двух поверхностных слоях, как ранее в уединен­ной шине, а в одном по­верхностном слое и это естественно, приводит к увеличению активного сопротивления шины в два раза.

В настоящем парагра­фе рассматривался вари­ант, в котором токи в шинах имели противопо­ложные направления. При формировании промыш­ленных шинопроводов часто используется парал­лельное соединение шин. Легко показать (рис. 29), что при таком способе соединения шин, при до­пущении h » a, h » b, напряженность уже на внутренних повер­хностях шин окажется равной нулю. Поэтому эквивалентное сопро­тивление двух шин будет определяться из расчета двойного повер­хностного слоя глубиной ∆. Но точно такое же сопротивление по­лучается и для уединенной шины, обтекаемой током I, т. е. при ярко выраженном эффекте близости наличие двух шин не умень­шает активное сопротивление системы.

Рис. 29