Квантовая электродинамика отличается очень высокой точностью прогнозов относительно свойств микрообъектов. Так, вычисленное на ее основе значение собственного магнитного момента электрона совпадает с экспериментально найденной величиной с точностью до 10-6.

1.6. Квантовые числа

Классическая механика, позволяющая охарактеризовать движение любого макрообъекта, оказывается принципиально неприменимой к описанию движения микрообъектов, в том числе электрона.

Квантово-механическое состояние электрона в атоме может быть охарактеризовано набором четырех квантовых чисел, которые определяют энергию (n), момент импульса (ℓ), проекцию момента импульса на заданное направление (mℓ) и проекцию спина на направление момента импульса (ms).

Рассмотрим более подробно каждое из квантовых чисел, представляющих собой по сути ключ к шифру, с помощью которого удается зашифровать квантовые состояния электрона.

Главное квантовое число (n) принимает значения в ряду целых чисел от 1 до бесконечности: 1, 2, 3, 4, 5,... и характеризует энергетический уровень электрона.

При n = 1 электрон находится в самом низком по энергии разрешенном состоянии. По мере возрастания n энергия электрона повышается. Условно принято нумеровать энергетические уровни с помощью значений главного квантового число (рис. 1.2.).

Электронам с одним и тем же главным квантовым числом n принято давать буквенные обозначения: электроны с n = 1 называют K-электронами, с n = 2 – L-электронами, с n = 3 – M-электронами и далее: N, O, P, Q. Этими же буквами обозначают оболочки в электронной структуре атома.

Главное квантовое число несет информацию и о размерах электронной орбитали: чем больше значение n, тем больше орбитальный радиус.

25

Е

_________ n = 3 (третий энергетический уровень)

Рис. 1.2. Энергетические уровни

Орбитальное квантовое число (ℓ) определяет геометрическую форму электронной орбитали и принимает целочисленные значения в ряду: 0, 1, 2, 3, ..., n-1 (где n – главное квантовое число). Каждому значению орбитального числа ℓ приписывают орбиталь определенной формы (рис. 1.3.) и обозначают ее латинскими буквами s (ℓ=0), p (ℓ=1), d (ℓ=2), f (ℓ=3)...(первые буквы от названий спектральных линий в спектре атома водорода: sharp, principal, diffuse, fundamental).

Изучение спектральных характеристик атомов выявило эффект расщепления спектральных линий, что потребовало введения наряду с понятием энергетических уровней соответствующего понятия энергетических подуровней. Значения орбитального квантового числа ℓ характеризуют энергетические подуровни электрона в пределах каждого энергетического уровня для многоэлектронного атома. Подуровни обозначаются теми же буквами: s, p, d и f.

Так, на первом энергетическом уровне (n = 1) имеется всего один подуровень s (ℓ = 0), на втором (n = 2) – два подуровня: s (ℓ = 0) и p (ℓ = 1) и т.д. (рис. 1.4).

-

26

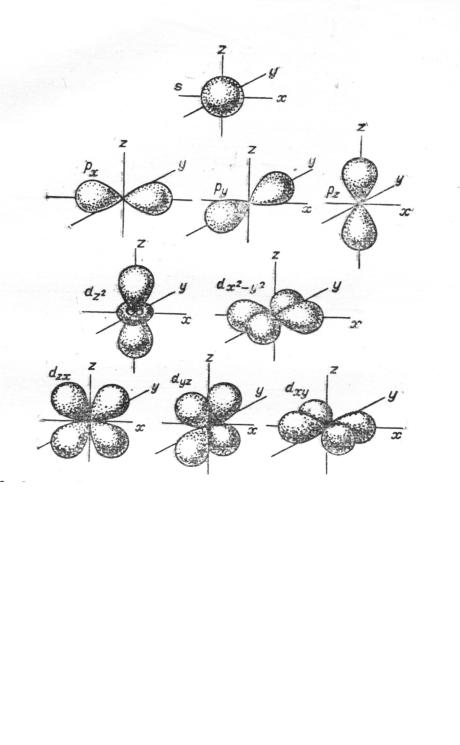
Рис. 1.3. Формы орбиталей

Рис. 1.4. Энергетические подуровни

Третье квантовое число называется магнитным квантовым числом (mℓ) и принимает целочисленные значения в диапазоне от -ℓ до + ℓ включительно: -

ℓ, ...-1, 0, +1, ... +ℓ .

27

Все орбитали, относящиеся к одному и тому же подуровню, в изолированном атоме при обычных условиях обладают одинаковой энергией. Орбитали, имеющие одинаковую энергию, называются вырожденными. В условиях, когда атом взаимодействует с другими атомами или с электрическим полем, пространственное расположение и энергия орбиталей могут изменяться.

Значения mℓ характеризуют разрешенные ориентации электронного облака в магнитном поле, под действием которого вырождение орбиталей снимается, и орбитальные энергии становятся квантовыми (дискретными). Число таких разрешенных ориентаций связано с геометрической формой орбиталей. Количество значений этого квантового числа позволяет определить число орбиталей на данном энергетическом подуровне.

Так, на s-подуровне (ℓ=0) – всего одна орбиталь (рис. 1.3.), характеризующаяся единственным значением магнитного квантового числа: mℓ = 0.

На p-подуровне (ℓ=1) – три орбитали (для ℓ=1 mℓ принимает три значения -1, 0 и +1), каждая из которых ориентирована: по оси х (орбиталь px), по оси у (орбиталь py) и по оси z (орбиталь pz) декартовой системы координат (рис. 1.3.). Оси трех соответствующих гантелеобразных орбиталей направлены под углом 900 друг к другу.

При ℓ=2 (d-подуровень) число mℓ имеет пять разрешенных значений: -2, - 1, 0, +1, +2 (рис. 1.3.). Пять d-орбиталей также обозначаются с помощью индексов, связанных с координатами x, y, z: dxy, dxz, dyz, dz2 и dx2-y2.

Буквой f обозначают подуровень с ℓ = 3 (f-подуровень), для которого магнитное квантовое число принимает семь значений: -3, -2, -1, 0, +1, +2, +3. Этот подуровень является совокупностью семи орбиталей.

Спиновое квантовое число (ms) – единственное квантовое число, не связанное с решениями уравнения Шредингера. При каждом заданном значении mℓ спиновое квантовое число принимает всего два значения: +½ и -½.

Спиновое квантовое число s характеризует величину спинового углового момента электрона. Магнитное спиновое квантовое число определяет направление спинового углового момента электрона.

28