Метрология / Том 1. Общие сведения. Основные параметры и требования. Конструктивные и силовые схемы / Glava4-4-1-Silovyje_skhemy_GTD

Глава 4 - Силовые схемы ГТД

При работе ГТД все его детали и узлы испытывают воздействие разнообразных нагрузок - газовых, центробежных, инерционных, вибрационных, акустических, от температурных деформаций, от крутящих и изгибающих моментов и др. Усилия от этих нагрузок передаются от детали к детали. В итоге усилия суммируются и передаются на внешнюю подвеску двигателя или взаимно компенсируются («уничтожаются») без передачи на наружные элементы ГТД. Детали и узлы, которые воспринимают основные внутренние усилия и по которым осуществляется их дальнейшая передача, называют силовыми. Совокупность силовых деталей и узлов определяет силовую схему двигателя.

Для удобства анализа работы деталей и узлов ГТД, входящих в силовую схему, применяется ее упрощенное графическое изображение. Обычно для таких схем используют условные изображения деталей и узлов, но обязательно показывают их взаимное расположение и наличие всех существующих связей между отдельными элементами. Силовая схема двигателя во многом зависит от конструктивных особенностей его узлов – компрессора, камеры сгорания и турбины, сопла, опор ротора, а также от выбора схемы крепления двигателя к самолету или к раме (наземные ГТУ). Как правило, при прочностных расчетах силовые схемы корпусов и роторов рассматривают отдельно.

При анализе работы деталей, входящих в силовую схему ГТД, необходимо учитывать их температурное состояние. Часть деталей нагрета до высокой температуры и, следовательно, температурные деформации этих деталей могут являться дополнительными нагружающими факторами.

Силовая схема ГТД позволяет представить общую картину взаимодействия отдельных силовых элементов двигателя, помогает определить усилия, действующие на конкретную деталь, что необходимо для оценки прочности и жесткости конструкции.

4.1- Усилия, действующие в ГТД

Âряде случаев усилия, действующие на детали ГТД, замыкаются внутри детали и внешне не проявляются. Это прежде всего относится к деталям, работающим в поле центробежных сил (диски, валы, рабочие лопатки компрессора и турбины). Такие усилия называются внутренними.

Усилия в узлах ГТД, в основном, передаются на соседние элементы силовой схемы, частично замыкаются внутри двигателя, а частично передаются через детали системы подвески на самолет. Так сила тяги передается на самолет как равнодействующая осевых составляющих сил, действующих на элементы силовой схемы двигателя. Усилия, не замыкающиеся внутри двигателя называют свободными.

Основные нагрузки можно разделить на три группы по природе возникновения:

-газовые - обусловлены перепадом давления

âгазовом тракте двигателя и изменением скорости и направления газового потока;

-массовые (силы инерции и инерционные моменты) - возникают при вращении роторов двигателя, при эволюциях самолета, при взлете и посадке, при наличии статического и динамического дисбалансов роторов;

-температурные - возникают из-за неравномерного нагрева и/или охлаждения деталей, различного коэффициента линейного расширения их материалов, а также при стеснении температурных деформаций.

Силы и моменты, действующие на узлы и детали двигателя, можно разделить на несколько видов по характеру деформации:

-растягивающие или сжимающие силы - возникают вследствие давления газов на детали двигателя и от действия центробежных сил вращающихся масс;

-изгибающие моменты - возникают от газовых сил, масс узлов и деталей, а также от инерционных сил;

-крутящие моменты - возникают в роторах от действия воздуха и газов на рабочие лопатки компрессора и турбины и в корпусных деталях от действия воздуха и газов на направляющие лопатки компрессора и сопловые лопатки турбины.

В зависимости от направления действия нагрузки могут быть разделены на осевые и поперечные, действующие в вертикальной и горизонтальной плоскостях. Моменты различного происхождения могут действовать вокруг всех трех осей – продольной (совпадающей с осью двигателя), вертикальной и горизонтальной.

4.1.1 - Осевые газовые силы

Осевое усилие Ðî, возникающее на элементах конструкции двигателя от газовых сил, определя-

Статические силы возникают из-за изменения статического давления Pñ газа во входном и выходном сечении элемента. Газодинамические силы возникают из-за изменения импульса газа (воздуха) при прохождении его через рассматриваемый элемент конструкции.

В общем случае усилие от статического давления определяется как:

ãäå ð - статическое давление в рассматриваемом сечении;

F - площадь рассматриваемого сечения. Динамическое усилие от изменения импуль-

са газа определяется как:

ãäå m - расход газа (воздуха);

V1 è V2 - скорость газа (воздуха) во входном и выходном сечениях рассматриваемого элемента.

Рассмотрим определение осевых сил в отдельных узлах и деталях ГТД.

За положительное направление сил примем направление движения воздуха (газа) в проточной части двигателя.

4.1.1.1 — Входное устройство двигателя

Определяем усилие на внутреннюю стенку входного устройства (см.Рис. 4.1).

Выбраны два сечения I-I – входное и II-II – выходное. Из газодинамического расчета в сечениях известны скорости воздуха (V1, V2)и статические давления (P1, Ð2).

Равнодействующая сил статического давления равна:

ãäå f1 è f2 – площадиíèé. входного и выходного сече- В нашем случае:

f1= (π / 4)d12,

(4.5)

f2=(π / 4)(d22 - d32).

Динамическая составляющая определяется по формуле (4.3).

Кроме того, на внешнюю стенку входного устройства действует осевая сила Ðâ, получающаяся от давления Ðâíåø воздуха на наружную стенку обтекателя (определяется расчетом или продувкой входного устройства в аэродинамической трубе).

Таким образом, суммарная осевая сила, действующая на входное устройство двигателя рассчи- тывается следующим образом:

Ðî âó= Ðc+Ðä+Ðâ= P1 f1 – Ð2 f2+ m(V2 - V1)+ Ðâ,

(4.6)

Рис. 4.1 – Схема действия статических сил во входном устройстве

4.1.1.2 — Осевой компрессор дискового типа

Для осевого компрессора дискового типа приложенная к ротору осевая сила определяется (см.Рис. 4.2):

ãäå Ðñòi – осевая сила, действующая на каждое рабочее колесо.

Осевая сила, действующая на отдельное рабочее колесо определяется следующим образом:

ãäå Ðñi – сумма статических давлений, действующих на рабочее колесо (т.е. на лопатки и диски);

Ðäi – газодинамическое усилие, вызванное изменением импульса воздуха при прохождении через лопатки.

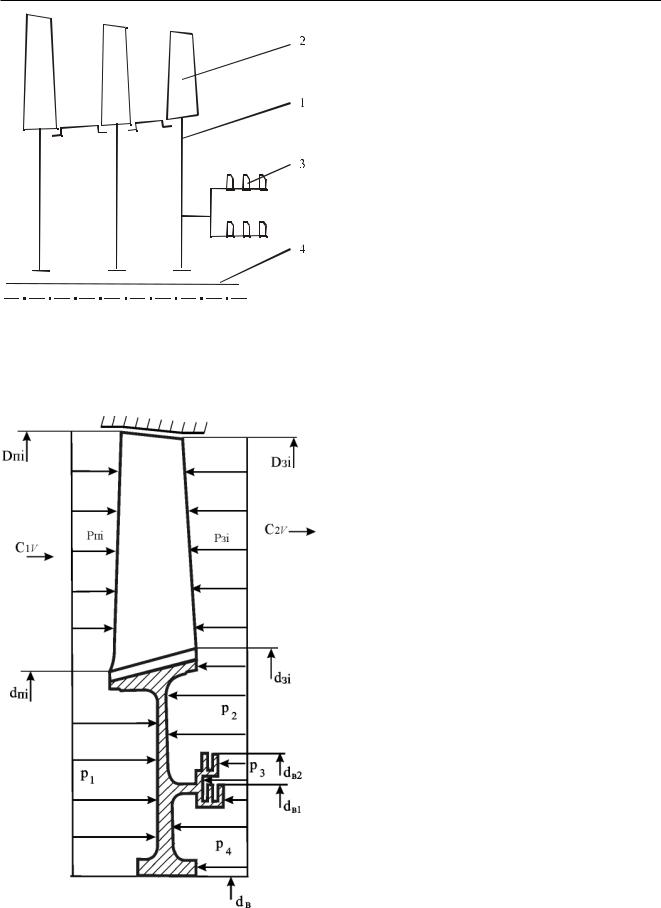
Рис. 4.2 – Схема осевого компрессора дискового типа 1 – диски; 2 – рабочие лопатки;

3 – лабиринтные уплотнения; 4 - вал

Рис. 4.3 – Схема действия статических сил на рабочее колесо осевого компрессора

В нашем примере рассмотрен вариант расче- та более сложного по конструкции рабочего колеса КВД с двухступенчатым лабиринтным уплотнением за рабочим колесом. Необходимо отметить, что в современных ГТД давление воздуха за компрессором достигает значительных величин - свыше 30 кгс/см2. Поэтому для минимизации утечек воздуха из проточной части применяются лабиринтные уплотнения из нескольких ступеней. Естественно, для рабочих колес промежуточных ступеней, где отсутствуют лабиринтные уплотнения, расчет суммы сил статических давлений значительно проще и представляет частный случай рассматриваемого примера.

Сумма сил статических давлений, действующих на рабочее колесо (см. Рис. 4.3), будет равна:

Ðñ= pïiπ /4( Dï i2-dï i2) + piπ /4(dïi2-dâ2) –

–pçi π /4(Dçi2-dçi2) – p2 π /4(dç12-dâ22) –

–p3π /4(dâ22- dâ12) – p4π /4(dâ12- dâ2)

(4.9)

Динамическая составляющая осевого усилия для рабочего колеса:

ãäå m – расход воздуха;

C2v è C1v – осевые составляющие скорости воздуха на входе и выходе из рабочего колеса.

Таким образом, осевое усилие на отдельном рабочем колесе осевого компрессора определяем как:

+ m (C2v – C1v)

(4.11)

Конструктивно изменяя диаметральное расположение лабиринтов, можно довольно в широких пределах варьировать величину осевой силы, действующей на диск. Таким методом широко пользуются при отстройке суммарного осевого усилия, передаваемого на опору ротора (раздел 4.1.1.6).

Осевое усилие, действующее на лопатки НА компрессора осевого типа, определяется аналогич- ным способом.

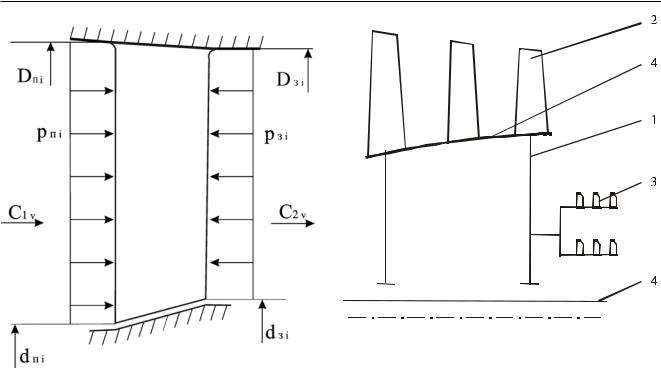
Рис. 4.4 – Схема действия статических сил на лопатку направляющего аппарата осевого компрессора

Осевая сила, действующая на проточную часть НА i ступени (см. Рис. 4.4), определяется так же, как и для рабочего колеса, по следующей формуле:

Pñòi = pïi (Dïi2 – dïi2) π /4 – pçi( Dçi2 – dçi2) π /4 +

Осевые силы на рабочие лопатки и НА компрессора действуют в сторону входа и достигают величин, в несколько раз превышающих тягу двигателя. Их определение необходимо для расчета на прочность и деформацию элементов конструкции роторов, корпусов осевого компрессора и опор.

Осевые силы вызывают растяжение ротора компрессора и корпуса. Усилия растяжения возрастают от первой ступени к последней, т.к. происходит сложение осевых сил ступеней.

Рис. 4.5 – Схема осевого компрессора барабанного типа 1 – диски; 2 – рабочие лопатки;

3 – лабиринтные уплотнения;

4 – барабан ротора; 5 - вал

Определение осевых усилий для осевых компрессоров барабанного типа (см. Рис. 4.5) производится по этой же методике, но оно упрощено, т.к. для средних ступеней компрессора нет необходимости определять перепады статических давлений на дисках.

4.1.1.3 — Камера сгорания

Осевые усилия, действующие на КС, определяются как сумма приложенных к ней статических и динамических усилий.

Для КС, изображенной на Рис. 4.6, осевая сила, действующая на внутренние поверхности, будет равна:

Pîêñ = mâV1 – mãV2 + P1 (Dï2 – dï2) π /4 -

ãäå P1, V1, P2, V2 – статические давления и скорости воздуха и газа на входе и выходе из КС;

– расход воздуха на входе в КС;

– расход газа на выходе из КС;

– геометрические размеры КС на входе и выходе.

Учитывая, что расход газа на выходе из КС больше расхода воздуха на входе в нее всего на 1…2 %, эту формулу можно упростить, т.е.:

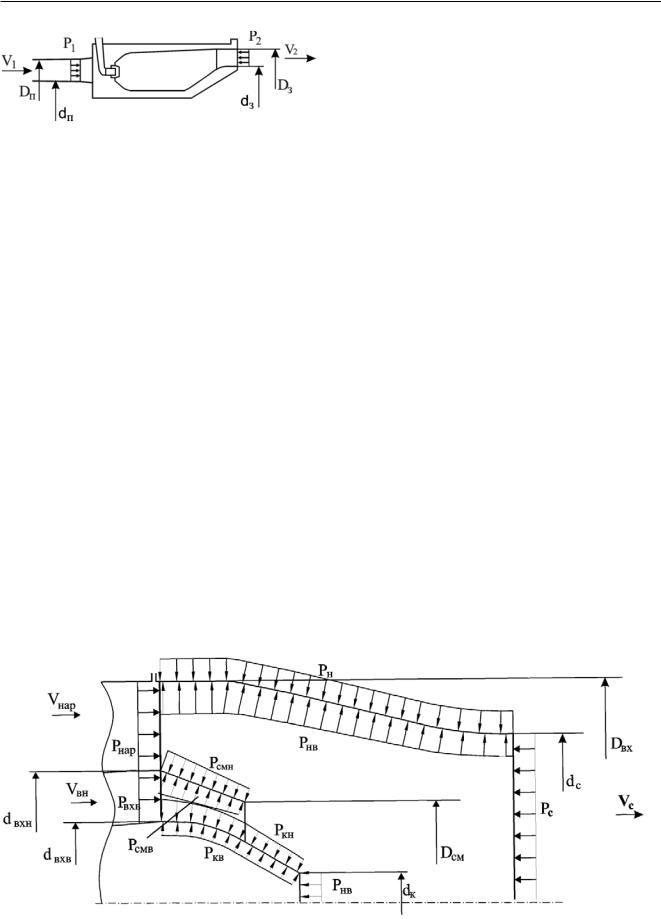
Рис. 4.6 – Схема действия осевых сил на КС

Осевая сила КС действует в сторону компрессора и достигает величины значительно превышающей величину тяги двигателя.

4.1.1.4 — Турбина

Осевое усилие от газовых сил, действующее на рабочее колесо и сопловые аппараты турбины, определяется точно так же, как и для компрессора, при этом осевая сила турбины всегда направлена в сторону сопла.

4.1.1.5 — Сопло

Осевое усилие, действующие на сопло, определяется как сумма осевых составляющих стати- ческих сил, действующих на разные элементы сопла, и динамических усилий потока воздуха (газа).

В наиболее сложном случае двухконтурного двигателя с внутренним смешением потоков осевая сила может быть определена следующим образом (для простоты расчетов примем, что смешение потоков воздуха наружного контура и газа внутрен-

него контура происходит мгновенно в плоскости смешения):

В свою очередь:

∑ Ðîñò = Ðîâõ-Ðîñð-Ðîê+Ðîâí+Ðîñì+Ðîê

(4.16) Определим величину каждой из составляю-

ùèõ.

Осевая равнодействующая сил статического давления на входе:

в сопло

Для упрощения расчетов наружный диаметр внутреннего контура на входе в сопло принимаем равным внутреннему диаметру канала наружного контура.

Осевая равнодействующая сил статического давления на выходе из сопла:

ãäå Ðñ - статическое давление газа на срезе сопла; dc – диаметр сопла.

Осевая равнодействуюшая сила на срезе сопла:

ãäå Ðíâ - среднее внутреннее статическое давление воздуха на наружную стенку сопла (для

упрощения примем Ðíâ = (Ðíàð + Ðñ)/2 Ðí - статическое наружное давление

(часто это давление принимается равным атмосферному, т.е. Ðí = Ðàòì).

Таким образом:

Ðîâí = π /4(Dâõ2 – dñ2)(Ðíàð + Ðñ – 2Ðàòì)/2

(4.21)

Аналогично определяется осевая составляющая сил статического давления на стенку смесителя:

смесителя.

После преобразований получим:

Ðîñì = π /4(dâõí2 – Dñì2)(Ðâí – Ðíàð)/2

(4.23) Осевая составляющая сил статического дав-

ления на внутренний корпус сопла:

Ðîê = π /4(dâõí2 – dê2)Ðêâ –

– π /4(dâõí2 – dê2)(Ðâí +Ðêâ)/2

(4.24)

ãäå (Ðâí +Ðêâ)/2 – среднее наружное статическое давление на корпус сопла.

После преобразований получим:

Ðîê = π /4(dâõâ2 – dê2)(Ðêâ – Ðâí)/2

(4.25) Сумма динамических усилий от потока воз-

духа и газа через сопло составит:

∑ Ð=(mâ íàð+ mã âí)Vc - mâ íàðVíàð – mã âí Vâí

(4.26)

– расход воздуха через наружный контур;

– расход газа через внутренний контур;

– скорость газа на срезе сопла;

– скорость воздуха в наружном контуре на входе в сопло;

– скорость газа во внутреннем контуре на входе в сопло.

Осевая сила, действующая на сужающееся реактивное сопло, всегда имеет направление «назад» (т.е. против полета для авиационных двигателей). На расширяющуюся часть сопла Лаваля осевое усилие имеет направление «вперед»

Предложенная выше модель расчета осевых сил, действующих на сопло, предназначена для относительно конструктивно сложного двухконтурного авиационного ГТД. Определение осевых сил для других конструкций сопла может рассматриваться как частный случай приведенной методики.

4.1.1.6 — Осевая сила

В газотурбинных двигателях вал турбины связан с валом компрессора, благодаря чему осевая сила компрессора в значительной степени уравновешивается осевым усилием турбины, а неуравновешенная часть осевого усилия воспринимается упорным подшипником ротора и передается через

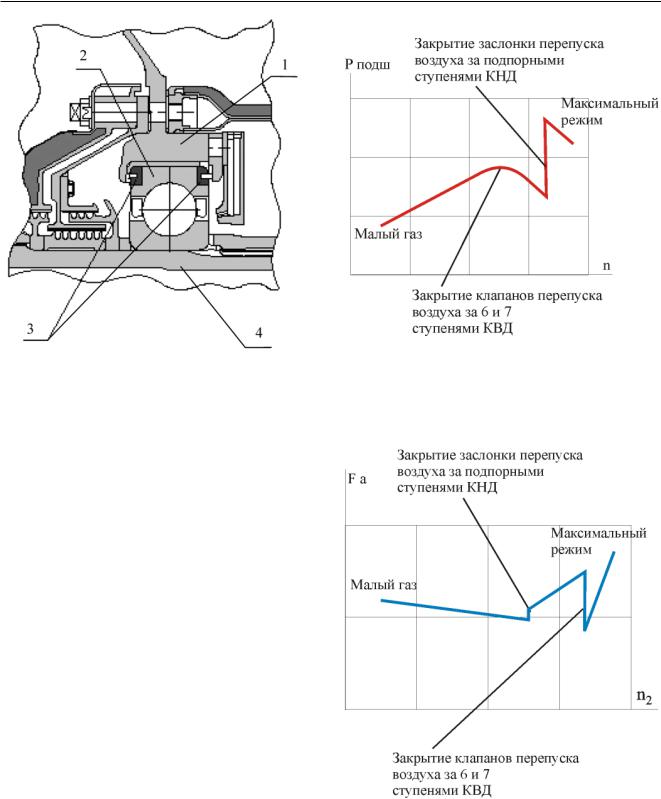
Рис. 4.9 – Опора шарикоподшипника с тензокольцами для замера осевого усилия 1 – опора (корпус); 2 – шарикоподшипник;

3 - кольца с тензодатчиками;

4 – âàë

На Рис. 4.10 в качестве примера показано фактическое изменение осевой силы на роторе низкого давления во всем диапазоне работы двигателя ПС-90А, замеренное во время наземных испытаний. Осевая сила при всех условиях работы направлена в одну сторону (по направлению полета).

Для объяснения характера изменения осевой силы, действующей на шарокоподшипник (далее просто ОС), напомним, что она является малой разностью больших усилий, действующих на роторы компрессора и турбины.

Осевые усилия, действующие на компрессор и турбину являются суммой большого числа газостатических и газодинамических сил, приложенных к отдельным элементам или деталям ротора. При изменении режима работы двигателя происходят непропорциональные изменения составляющих осевого усилия. Особенно заметное влияние на эти изменения оказывают закрытие (открытие) отборов воздуха за различными ступенями компрессора, связанное с необходимостью повышения устойчивости работы КВД и КНД на различных режимах работы двигателя. Как видно из Рис. 4.10 на низких режимах работы двигателя, до закрытия клапанов перепуска за 6 и 7 ступенями КВД, по мере увеличения режима работы и параметров двигателя более интенсивным был рост

Рис. 4.10 – Осевая сила на роторе низкого давления двигателя ПС-90А

Рис. 4.11 – Осевая сила на роторе высокого давления двигателя ПС-90А

газовых сил «компрессорной» части ротора и суммирующее усилие («осевая сила») направленное «вперед» также увеличивалось. После закрытия клапанов перепуска за 6 и 7 ступенями КВД, более

интенсивным стал рост газовых сил «турбинной» части ротора и осевая сила стала уменьшаться при увеличении режима работы. Эта закономерность сохранилась несмотря на скачкообразное увеличе- ние осевой силы в момент закрытия заслонок перепуска воздуха за КНД.

Аналогичным образом можно объяснить изменение осевой силы, действующей на шарикоподшипник ротора ВД, хотя характер изменения ее противоположен (см. Рис. 4.11).

Сумма осевых усилий, приложенных к различ- ным узлам двигателя, численно равна тяге, развиваемой ГТД.

На Рис. 4.12 показано расчетное распределение сил, действующих на узлы двигателя ПС-90А на максимальном режиме работы в земных условиях. Внутренние усилия в элементах конструкции двигателя значительно превышают те усилия, которые передаются на силовые элементы самолета или рамы (для наземных установок). Правильное определения этих усилий, построение реальных схем воздействия сил на каждую отдельную основную деталь силовой схемы двигателя позволит принимать оптимальные решения как с точки зрения прочностных и ресурсных, так и с точки зрения массовых показателей для этих деталей.

4.1.2 - Крутящие моменты от газовых сил

C достаточной точностью крутящие моменты от газовых сил, возникающие на лопатках рабочих колес (РК) и НА можно вычислить на основе треугольников скоростей на среднем радиусе ступени перед и за соответствующими элементами [4.1]. Таким образом, для РК и НА компрессора (см. Рис. 4.13) расчетные формулы можно записать:

радиусе.

Как видно из формул, крутящие моменты равны разности моментов количеств движения воздуха относительно оси вращения ротора.

Рисунок 4.13 — Определение крутящего момента на лопатках компрессора

Для РК момент имеет положительный знак, что означает подвод энергии к воздушному потоку и увеличение кинетической энергии вращательного движения воздуха. Окружное усилие и момент на рабочем колесе от воздействия воздуха направлены против направления вращения.

Для НА момент получается с отрицательным знаком, что означает уменьшение кинетической энергии вращательного движения и переход ее в давление. Окружное усилие и момент, действующие на НА, направлены в сторону вращения РК.

Крутящие моменты, действующие на ротор и корпус компрессора, суммируются начи- ная с первой ступени. Наибольшие крутящие моменты действуют за последней ступенью компрессора. Крутящий момент для любого промежуточного сечения ротора или корпуса определяется как сумма моментов всех предыдущих ступеней. Расчет этих моментов необходим для оценки прочности элементов конструкций ротора и корпуса.

Величины крутящих моментов, действующих на ротор и статор турбины, определяются аналогич- ным образом. Но процессы, происходящие в турбине, носят противоположный характер, а следовательно - направление действия крутящего момента будет направлено в другую сторону.

4.1.3 — Инерционные силы и моменты

Инерционные силы и моменты возникают в деталях двигателя от статической и динамической неуравновешенности роторов, а также от изменения скорости и траектории самолета, на котором закреплен двигатель.

Неуравновешенные силы и моменты роторов двигателя передаются на корпуса через подшипниковые опоры. Направление действия этих сил меняется во времени, а величины этих сил пропорциональны квадрату частоты вращения ротора. Благодаря высокой точности балансировки роторов амплитуды этих сил и моментов невелики. Однако, действуя с высокой частотой, они способны вызывать вибрации корпусов и усталостные повреждения в них. Более подробно вопросы статической и динамической неуравновешенности роторов рассмотрены в разделе 14.5.

При разгоне и торможении самолета появляется дополнительная осевая сила (к силе обусловленной газовыми нагрузками), нагружающая ротор двигателя и передаваемая на корпус через упорные подшипники. Значение этой силы может превышать массу ротора в несколько раз. Кроме того, эта дополнительная сила нагружает узлы крепления двигателя к самолету.

При отклонении траектории полета самолета от прямолинейной возникает угловое ускорение, которое вызывает гироскопический момент и инерционные перегрузки. Величина гироскопического момента пропорциональна угловому ускорению и частоте вращения ротора и может быть определена как:

При отсутствии точных данных момент инерции ротора (кг см сек) можно определять приближенно по формуле: