2.3. Напряженность электрического поля в диэлектрике

Для количественного описания поля в диэлектриках внесем диэлектрик в однородное электростатическое поле. Поле создается двумя бесконечными равномерно заряженными плоскостями. Пластинка из однородного диэлектрика расположена как на рис. 2.4.

Заряды, входящие в состав диполей диэлектриков, называются связанными. Под действием электрического поля они не могут покинуть пределов молекулы, в состав которой входят, а лишь смещаются из своих положений равновесия. Поляризация диэлектриков сопровождается появлением поверхностных зарядов на его границах.

В тех местах, где линии напряженности выходят из диэлектрика, на поверхности возникают положительные связанные заряды, то есть положительные заряды смещаются по полю, отрицательные –против поля (рис. 2.4) Таким образом, на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью (+),а на левой – избыток отрицательного заряда с поверхностной плотностью (–). Плотность связанных зарядов определяет поляризованность диэлектрика:.

Таким образом, появление нескомпенсированных поверхностных связанных зарядов приводит к возникновению внутри диэлектрика дополнительного электрического поля с напряженностью(поле, созданное двумя бесконечными заряженными плоскостями, т.е. гранями), которое направлено против внешнего поля и ослабляет его

. (2.4)

Внешнее поле – это поле, созданное свободными зарядами, в данном случае бесконечными заряженными пластинами.

Напряженность внешнего поля определяется по формуле

. (2.5)

Результирующая напряженность поля внутри диэлектрика равна:

или в скалярном виде с учетом направления

. (2.6)

Напряженность электрического поля определяется всеми зарядами: и сторонними , и связанными. С учетом (2.4) и (2.5) можно записать

. (2.7)

Так как поверхностная плотность связанных зарядов меньше поверхностной плотности свободных зарядов, то не все поле компенсируется зарядами диэлектрика, часть линий напряженности поля пройдет сквозь диэлектрик, другая же обрывается на связанных зарядах (рис. 2.4).

Рис. 2.4. Диэлектрик в однородном электростатическом поле

Следовательно, результирующее поле внутри диэлектрика меньше, чем внешнее поле. Величина, показывающая во сколько раз поле в вакууме больше, чем поле в диэлектрике, называется относительной диэлектрической проницаемостью вещества .

Относительная диэлектрическая проницаемость связана с диэлектрической восприимчивостью вещества

. (2.8)

Отсюда следует, что диэлектрическая проницаемость больше диэлектрической восприимчивости для всех веществ.

Таким образом, результирующее поле внутри диэлектрика будет определяться по формуле

. (2.9)

Следовательно, относительная диэлектрическая проницаемость ε характеризует электрические свойства диэлектрика, т.е. способность диэлектрика к поляризации.

2.4. Теория метода

Эквивалентная схема электрической цепи для измерения относительной диэлектрической проницаемости представлена на рис. 2.5.

C R

~ u₀

Рис. 2.5. Схема электрической цепи

для измерения относительной диэлектрической проницаемости

Реактивное сопротивление конденсатора цепи переменного синусоидального тока определяется выражением

, (2.10)

где C – емкость конденсатора,  – частота переменного напряжения (тока).

Величину переменного тока можно определить по закону Ома, обобщенного для цепей переменного тока:

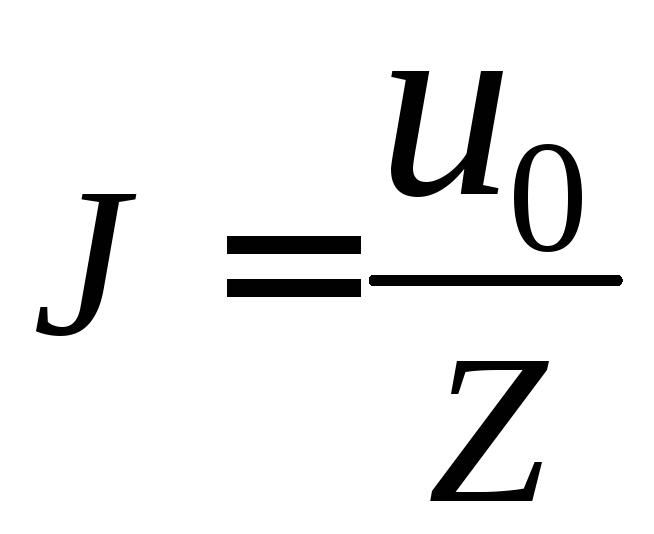(2.11)

или

, (2.12)

где u₀ – напряжение на выходе генератора, Z – полное сопротивление цепи, R – активное сопротивление, u – падение напряжения на активном сопротивлении, регистрируемое цифровым вольтметром.

Возведя выражение (2.11) в квадрат получим:

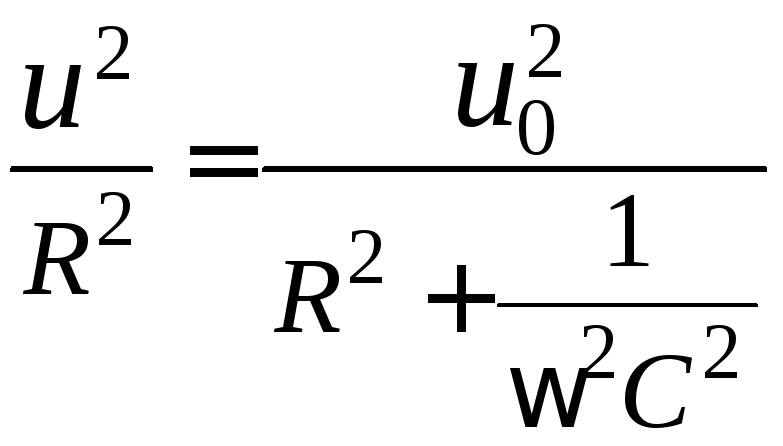, (2.13)

откуда

.

Используя формулу для расчета емкости плоского конденсатора

, (2.14)

можно получить выражение для вычисления относительной диэлектрической проницаемости

. (2.15)

Если величины R и С подобрать таким образом, чтобы в используемом диапазоне частот выполнялось условие: , то значениемu в подкоренном выражении соотношения (2.16) можно пренебречь, так как u << u₀.

Тогда выражение (2.16) можно упростить и представить в виде

. (2.17)