Лабораторная работа № 3

Измерение длины световой волны с помощью дифракционной решетки

1. Цели и задачи работы

Цели работы:

• Ознакомление студентов с методикой измерения длины световой волны с помощью дифракционной решетки.

Задачи работы:

• Измерить длину световой волны с помощью дифракционной решетки.

• Определение погрешности измерений.

2. Теоретическая часть

Дифракционная решетка представляет собой совокупность большого числа очень узких параллельных щелей, разделенных непрозрачными промежутками. Общая ширина щели и непрозрачного промежутка называется периодом решетки. Например, если на дифракционной решетке имеется 100 штрихов на 1 мм, то период, или постоянная дифракционной решетки равна .

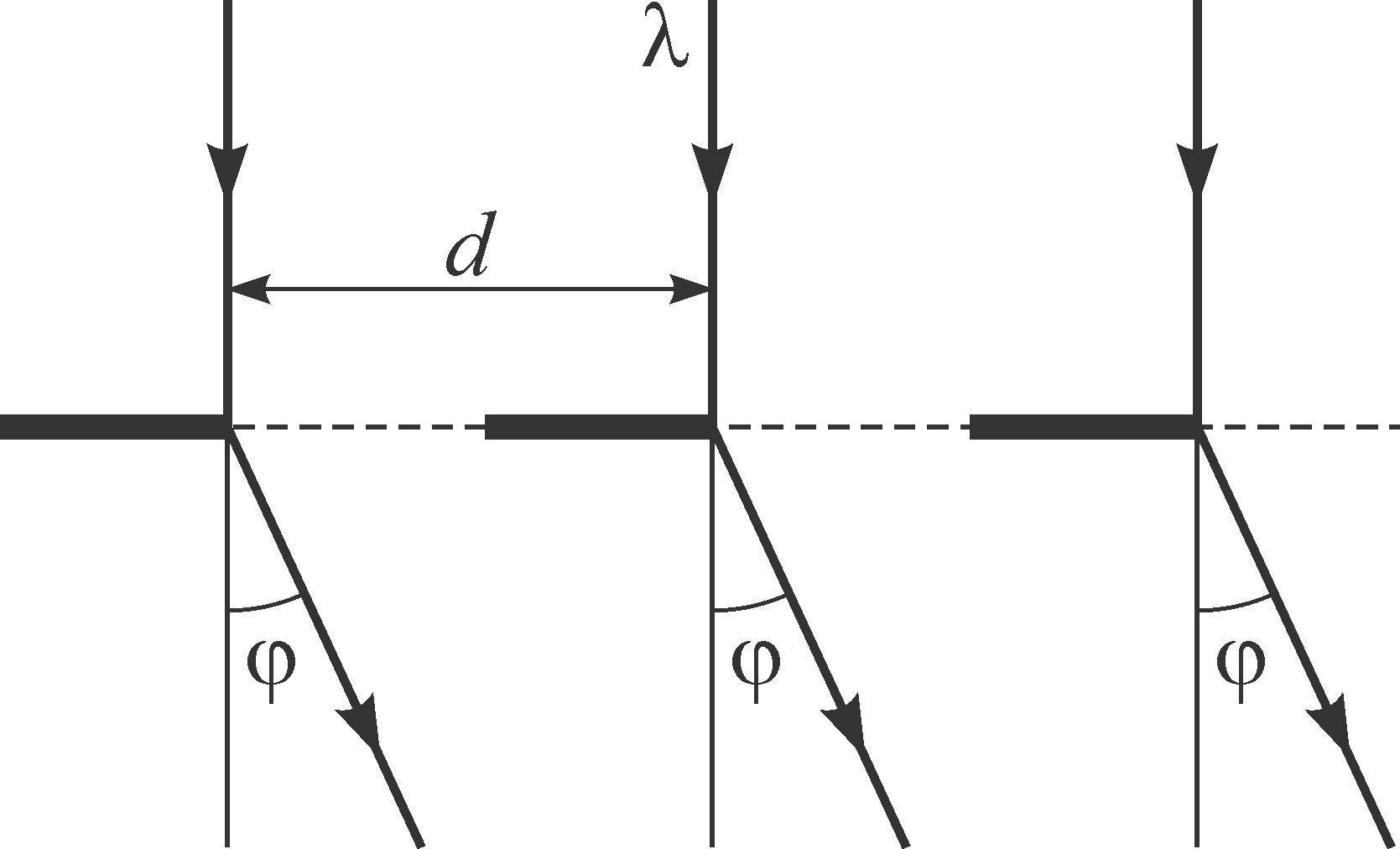
На рис. 8 представлена схема хода лучей через решетку. Лучи, проходящие через решетку перпендикулярно ее плоскости, попадают в зрачок наблюдателя и образуют на сетчатке глаза обычное изображение источника света. Лучи, огибающие края щелей решетки, в соответствии с принципом Гюйгенса, имеют некоторую разность хода, зависящую от угла . Если эта разность пропорциональна k, где k – целое число, то каждая такая пара лучей образует на сетчатке изображение источника, цвет которого определяется соответствующей длиной волны .

Смотря сквозь решетку на источник света, наблюдатель, кроме этого источника, видит расположенные симметрично по обе стороны от него дифракционные спектры. Ближайшая пара спектров (1-го порядка) соответствует разности хода лучей, равной  для соответствующего цвета. Более удаленная пара спектров (2-го порядка) соответствует разности хода лучей равной 2 и т.д.

Рис. 8. Ход лучей через дифракционную решетку

На оптической скамье может передвигаться пластина, в которой прорезана щель 1 прямолинейной формы (рис. 9). На пластине укреплена шкала с делениями. Щель освещается электрической лампочкой 2. Между лампочкой и щелью вставляется монохроматический светофильтр. На другом конце оптической скамьи укреплен держатель 3, в который вставляется дифракционная решетка 4. Если смотреть на освещенную монохроматическим светом щель через дифракционную решетку, то по бокам ее видна дифракционная картина.

Пусть каждое боковое дифракционное изображение смещено в сторону на величину S. Из рис. 9 видно, что , где R – расстояние от решетки до щели 1.

Рис. 9. Схема установки

Так как угол  мал, то можно с достаточной степенью точности заменить на , т.е. .

Сравнивая последнее выражение с условием главного дифракционного максимума , получаем расчетную формулу для нахождения длины световой волны:

.

(1)

1. Приборы и принадлежности:

• Дифракционная решетка – 1 шт.

• Шкала со щелью – 1 шт.

• Источник света – 1 шт.

• Линейка – 1 шт.

• Светофильтры – 7 шт.

4. Порядок выполнения работы

1. Поместить дифракционную решетку с периодом в рамку прибора и укрепите его на подставке.

2. Включить источник света. Смотря через дифракционную решетку, увидеть по обе стороны щитка на черном фоне заметные дифракционные спектры нескольких порядков. В случае наклонного положения спектров повернуть решетку на некоторый угол до устранения перекоса.

3. Установить шкалу на расстояние R от дифракционной решетки.

4. Вставить в рамку светофильтр, начиная с красного и по шкале щитка рассматриваемой через решетку, определить расстояние S от щели до наблюдаемых линий 1-го и 2-го порядка. Результаты измерений занести в таблицу 6.

5. Проделать п. 4 для лучей другого цвета вставляя в рамку остальные светофильтры.

6. Проделать пп. 4 – 5 три раза перемещая шкалу на расстояние R 10 – 15 см.

7. Определить длину световой волны по формуле (1) для всех цветов лучей и занести в таблицу 6. Вычислить среднюю арифметическую длину каждой световой волны.

8. Рассчитать абсолютную и относительную погрешность измерения.

Таблица 6. Длина световой волны различных цветов

k

R, мм

S, мм

, нм

К

О

Ж

З

Г

С

Ф

К

О

Ж

З

Г

С

Ф

1

2

Среднее значение длины волны

5. Контрольные вопросы

1. В чем заключается принцип Гюйгенса-Френеля?

2. Какие волны называются когерентными?

3. Что называется дифракцией света? Как объясняется это явление?

4. Каков порядок следования цветов в дифракционных спектрах? Какова окраска нулевого максимума?

5. Чем отличаются дифракционные спектры, даваемые решетками с одинаковым количеством щелей, но с различными постоянными, и решетками с одинаковыми постоянными, но с различным количеством щелей?

6. Как изменится действие дифракционной решетки, если ее поместить в воду?

7. Как объяснить образование дифракционного спектра от одной щели на экране от лучей, прошедших через щель? От чего зависит распределение интенсивности в центре экрана?

8. Одномерная дифракционная решетка. Как объясняется образование дифракционной картины на экране? В каких точках наблюдаются максимумы интенсивности, в каких минимумы и почему?

9. Чем отличаются дифракционные картины при освещении решетки монохроматическим светом и белым светом? Как объяснить эти явления?

10. Что такое интерференция света? Участвует ли это явление при образовании дифракционного спектра на щели или решетке?

11. Белый свет падает нормально на одномерную дифракционную решетку, содержащую 100 щелей на 1 мм. Как распределится интенсивность света на экране? Сколько дополнительных минимумов между двумя главными максимумами образуется на экране? Каковы условия образования главных максимумов и главных минимумов?

12. Белый свет падает нормально на дифракционную решетку и на тонкую линзу большего диаметра. Как объяснить картины, образовавшиеся на экране при прохождении света через линзу и дифракционную решетку?

13. Каковы длины волн видимого света? Подвержены ли они дисперсии?

14. От чего зависит ширина полос дифракционного спектра? Что наблюдается на экране, если ширина щели намного больше длины волны ? Как объясняется это явление?

15. Что называется линейной и угловой дисперсией дифракционной решетки?

16. Что называется разрешающей силой дифракционной решетки?

17. Приведите пример дифракционных картин, получающихся для двух спектральных линий с помощью решеток, отличающихся разрешающей силой и линейной дисперсией.

5