
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
2 |
1 |
0 |
1 |
2 |
3 |
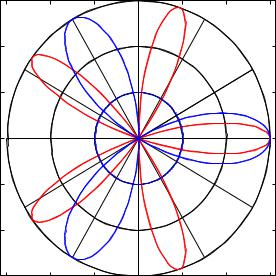
Рис. 4: Графики функций = 3cos(5') и 1 = 3cos(3') в полярных координатах |
||||||
4Построения в пространстве
Для построения поверхностей в gnuplot применяется команда splot. Обращение к ней происходит аналогично команде plot, за исключением некоторых особенностей. Выделим некоторые команды, применяемые исключительно к объемным построениям (их описание см. в построениях):
set zrange [<нач. значение>:<конечн. значение>] set surface
set pm3d
set palette <параметры настройки цвета>
set view <поворот по x> <поворот по z> <масштаб> <масштаб по z> set contour base|surface
set isosamples <целое число>
Следует отметить, что при параметрических построениях в пространстве в качестве параметров выступают переменные u,v. В остальном все так же, как и в случае плоскости.
Выполним некоторые построения.
set terminal postscript eps enhanced color set output "splot3.eps"
set grid
set xrange [-10:10] set yrange [-10:10] splot x*y
7

100
50
0
-50
-100
 10
10
5
-10 |
0 |
|
-5 |
||
|
||
0 |
-5 |
|
|
5 |
-10 10
Рис. 5: Поверхность, заданная функцией z = x y
set terminal postscript eps enhanced color |
|
|
set output "splot4.eps" |
|
|
set grid xtics ytics ztics |
# вкл. сетку по всем осям |
|
set xlabel "x" |
|
|
set ylabel "y" |
|
|
set key top |
# поместить легенду вверху |
|
set border 4095 |
# отобразить границы бокса |
|
set xrange [-15:15] |
|
|
set yrange [-15:15] |
|
|
set zrange [-0.25:1] |
# вид по оси Oz |
|
set pm3d |
# заливка поверхности палитрой |
|
set palette defined ( 1 "blue", 1 "yellow", 2 "red" ) |
# настройка палитры RGB |
|
splot sin(sqrt(x**2+y**2))/sqrt(x**2+y**2) ls 6 |
|
|
|
|
sin(sqrt(x**2+y**2))/sqrt(x**2+y**2) |
|
|
|
|
0.6 |
|
|
|
0.5 |
1 |
|
|
0.4 |
0.8 |
|
|
0.3 |
|
|
0.2 |
|
0.6 |
|
|
|
|
|
0.1 |
|
|
|
|
|
0.4 |
|
|
0 |
0.2 |
|
|
-0.1 |
|
|
-0.2 |
|
0 |
|
|
|
|
|
-0.3 |
|
|
|
|
|
-0.2 |
|
|
|
|
|
|
15 |
|
|
|
10 |
-15 |
|
|
5 |
|
|
0 |
|
-10 |
|
|
|
|
-5 |
y |
|
-5 |
0 |
||
|
-10 |
|
|
|
5 |
|
|
x |
10 |
-15 |
|
|
|
15 |
|
p
sin x2 + y2
Рис. 6: Поверхность, заданная функцией z = p
x2 + y2
8
set terminal postscript eps enhanced color set output "splot4_1.eps"
unset key |
|
unset pm3d |
# откл. заливку поверхности |
unset surface |
# откл. сетку поверхности |
unset colorbox |
# откл. вывод colorbox-а (см. рис.) |
set contour surface |
# линии уровня на поверхности |
unset xlabel |
|
unset ylabel |
|
unset ztics |
|
set zrange [-0.25:1] |
|
set samples 300 |
|
set view 0,0,1,1 |
# вид сверху |
splot sin(sqrt(x**2+y**2))/sqrt(x**2+y**2) lw 2
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
-15 |
|
|
|
|
-15 |
-10 |
-5 |
0 |
5 |
10 |
15 |
|
p |
|
|
|
|
|
|
|
|
|
sin |
+ y |
|
|
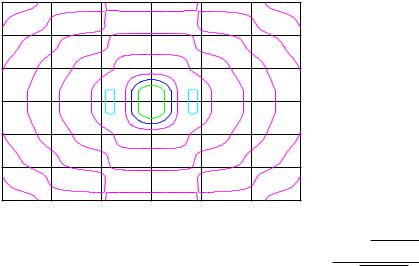
Рис. 7: Линии уровня поверхности, заданной функцией z = |
p |
|
|
|||||||
|
|
|
|
|
|
|
|
x2 |
|
2 |
set terminal postscript eps enhanced color set output "splot6.eps"
unset key unset pm3d
set grid xtics ytics ztics set samples 100
set parametric
splot [-2*pi:2*pi] cos(u)*cos(v),cos(u)*sin(v),sin(u)
9
1
0.8
0.6
0.4
0.2
0 -0.2 -0.4 -0.6 -0.8
-1
1
0.8
0.6
-1 |
|
|
|
|
|
|
|
|
0.4 |
-0.8 -0.6 |
|
|
|
|
|
|
|
0.2 |
|
|
-0.4 |
|
|
|
|
|
|
0 |
|
|
|
-0.2 |
|
|
|
|
|
-0.2 |
|
|
|
|
0 |
|
|
|
|
-0.4 |
|
|
|
|
|
0.2 |
|
|
|
||
|
|
|
|
|
0.4 0.6 |
|
|
-0.6 |
|
|
|
|
|
|
|
0.8 |
|
-0.8 |
|
|
|
|
|
|
|
|
1 |
-1 |
|
|
|
|
|
|
|
|
|
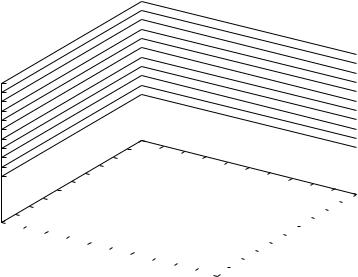
Рис. 8: Эллипсоид, заданный параметрически
5Использование дискретных данных
Одной из отличительных особенностей gnuplot является то, что формировать данные для построения графиков можно не только задавая промежутки изменения переменных, но и делая это вручную, причем можно как использовать заранее подготовленный файл с данными, так и вводить их в интерактивном режиме ’на лету’. Рассмотрим первый вариант (данные из файла).
В качестве примера зададим матрицу значений в текстовом файле, после чего произведем построение в gnuplot. Итак, создаем в директории ngnuplotnbinn файл mtrx1 и в нем:
1 1 |
5 |
# данные в виде матрицы ixj, i=1,j=1 |
1 2 |
-3 |
# i=1,j=2... |
1 3 |
-8 |
|
2 1 |
-4 |
|
2 2 |
6 |
|
2 3 |
1 |
|
Затем в командной строке gnuplot:
set terminal postscript eps enhanced color set output "splot7.eps"
splot "mtrx1" lw 3 # строим график по дискретным данным
10

"mtrx1.txt"
6
4
2
0
-2
-4
-6
-8
3
2.5
1 |
2 |
|
1.2 |
||
|
||
1.4 |
1.5 |
|
1.6 |
||
|
||
1.8 |
1 |
|
2 |
Рис. 9: Точечный график: визуализация данных из файла
В том случае если данные представлены в текстовом файле mtrx2 в виде матрицы
1 2 |
1 3 |
|
-1 3 1 |
-4 |
|
1 2 |
-3 |
4 |
5 1 |
1 5 |
|
..то команда для построения графика будет иметь вид:
set terminal postscript eps enhanced color set output "splot8.eps"
splot "mtrx2" matrix lw 3 # строим график по дискретным данным
11
