9 Transforms

the distance between the vertex of the fan-beam projections and the center of rotation when the projection data was created. For example, this code recreates the image I from the projection data P and distance D.

I = ifanbeam(P,D);

By default, the ifanbeam function assumes that the fan-beam projection data was created using the arc fan sensor geometry, with beams spaced at 1 degree angles and projections taken at 1 degree increments over a full 360 degree range. As with the fanbeam function, you can use ifanbeam parameters to specify other values for these characteristics of the projection data. Use the same values for these parameters that were used when the projection data was created. For more information about these parameters, see “Computing Fan-Beam Projection Data” on page 9-37.

The ifanbeam function converts the fan-beam projection data to parallel-beam projection data with the fan2para function, and then calls the iradon function to perform the image reconstruction. For this reason, the ifanfeam function supports certain iradon parameters, which it passes to the iradon function. See “The Inverse Radon Transformation” on page 9-29 for more information about the iradon function.

Reconstruct Image From Fanbeam Projections

The commands below illustrate how to use fanbeam and ifanbeam to form projections from a sample image and then reconstruct the image from the projections. The test image is the Shepp-Logan head phantom, which can be generated by the phantom function. The phantom image illustrates many of the qualities that are found in real-world tomographic imaging of human heads.

1Generate the test image and display it.

P = phantom(256); imshow(P)

9-40

Fan-Beam Projection Data

2Compute fan-beam projection data of the test image, using the FanSensorSpacing parameter to vary the sensor spacing. The example uses the fanbeam arc geometry, so you specify the spacing between sensors by specifying the angular spacing of the beams. The first call spaces the beams at 2 degrees; the second at 1 degree; and the third at 0.25 degrees. In each call, the distance between the center of rotation and vertex of the projections is constant at 250 pixels. In addition, fanbeam rotates the projection around the center pixel at 1 degree increments.

D = 250;

dsensor1 = 2;

F1 = fanbeam(P,D,'FanSensorSpacing',dsensor1);

dsensor2 = 1;

F2 = fanbeam(P,D,'FanSensorSpacing',dsensor2);

dsensor3 = 0.25

[F3, sensor_pos3, fan_rot_angles3] = fanbeam(P,D,...

'FanSensorSpacing',dsensor3);

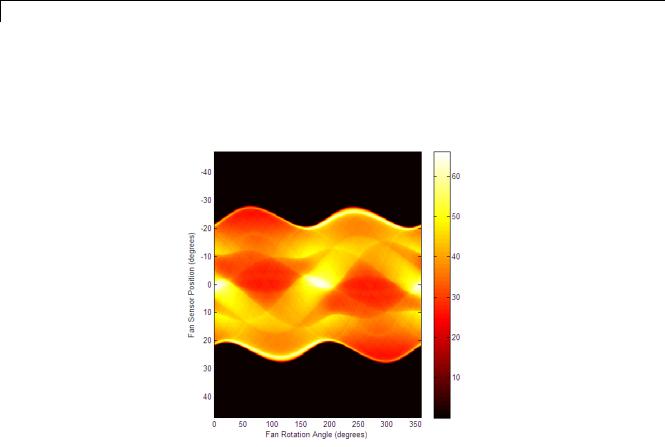
3Plot the projection data F3. Because fanbeam calculates projection data at rotation angles from 0 to 360 degrees, the same patterns occur at an

offset of 180 degrees. The same features are being sampled from both sides. Compare this plot to the plot of the parallel-beam projection data of the head phantom using 90 projections in “Reconstruct Image from Parallel Projection Data” on page 9-32.

figure, imagesc(fan_rot_angles3, sensor_pos3, F3)

9-41

9 Transforms

colormap(hot); colorbar

xlabel('Fan Rotation Angle (degrees)') ylabel('Fan Sensor Position (degrees)')

4Reconstruct the image from the fan-beam projection data using ifanbeam. In each reconstruction, match the fan sensor spacing with the spacing used when the projection data was created in step 2. The example uses the OutputSize parameter to constrain the output size of each reconstruction to be the same as the size of the original image |P|.

output_size = max(size(P));

Ifan1 = ifanbeam(F1,D, ...

'FanSensorSpacing',dsensor1,'OutputSize',output_size); figure, imshow(Ifan1)

Ifan2 = ifanbeam(F2,D, ...

'FanSensorSpacing',dsensor2,'OutputSize',output_size); figure, imshow(Ifan2)

9-42

Fan-Beam Projection Data

Ifan3 = ifanbeam(F3,D, ...

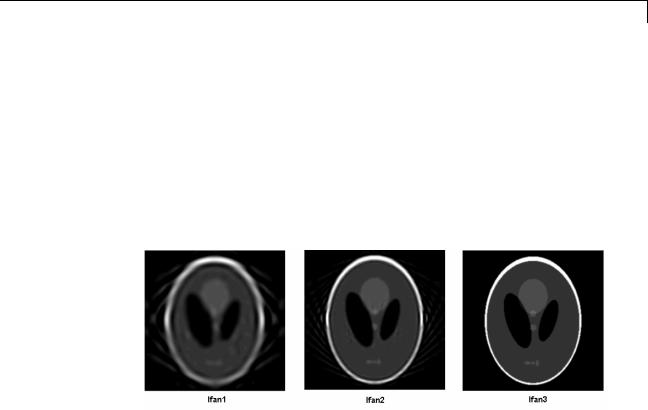
'FanSensorSpacing',dsensor3,'OutputSize',output_size); figure, imshow(Ifan3)

The following figure shows the result of each transform. Note how the quality of the reconstruction gets better as the number of beams in the projection increases. The first image, Ifan1, was created using 2 degree spacing of the beams; the second image, ifan2, was created using 1 degree spacing of the beams; the third image, ifan3, was created using 0.25 spacing of the beams.

Reconstructions of the Head Phantom Image from Fan-Beam Projections

9-43

9 Transforms

9-44