4.3. Оборудование

Прибор Лермонтова с исследуемой проволокой, набор грузов, микрометр.

4.4. Порядок выполнения работы

1. Измерить длину проволоки и ее диаметр, необходимый для определения площади поперечного сечения . Диаметр измерить в нескольких местах и для расчетов взять среднее значение.

2. Отрегулировать микрометр, вращая опорный винт, чтобы при отсутствии нагрузки на проволоке, стрелка микрометра была на нуле шкалы.

3. Последовательно нагружая проволоку грузами массой , произвести измерения. Разгрузку нити произвести в обратном порядке с повторным отсчетом показаний микрометра для каждой нагрузки и занести в табл. 11.

Таблица 11

№	, Н	, м	, Н/м2	, м	, м		ср, м		, Н/м2
					прямое	обратное
1
2
…

4. Вычислить значения по формуле (4.1), значенияпо формуле (4.2). Учесть, что в данном случае действующая сила является силой тяжести.

4. Вычислить значения по формуле (4.3) и среднее значение модуля Юнга_ср. Определить среднюю абсолютную и относительную погрешности измерений и результат представить в виде

Н/м²,

4. Построить график зависимости оти убедиться, что между ними имеется линейная зависимость. Определить значение_ср из построенного графика.

Контрольные вопросы

1. В чем заключается явление деформации? Приведите примеры.

2. Какие виды деформации вы знаете? Чем они отличаются друг от друга?

3. Что называют абсолютной величиной деформации и относительной деформацией?

4. Как формулируется закон Гука? Какие физические величины он связывает?

5. В чем состоит физический смысл коэффициента упругости и модуля упругости?

6. В чем состоит физический смысл модуля Юнга?

7. Какие деформации называют упругими? Что называют пределом прочности? Нарисуйте диаграмму напряжений для какого-нибудь вещества и на нем покажите области, соответствующие пределу упругости, пределу текучести и пределу прочности.

8. Как объяснить явление деформации с точки зрения молекулярного строения вещества?

9. Приведите примеры технического применения явления деформации.

Лабораторная работа № 5

Определение коэффициента Пуассона воздуха методом адиабатического расширения

5.1. Цели и задачи работы

Целью работы является:

• Изучение метода определения коэффициента Пуассона.

Задачей работы является:

• Определение коэффициента Пуассона воздуха по данным измере­ния его давления после адиабатического расширения и последующе­го изохорного нагревания.

5.2. Теоретическая часть

5.2.1. Теплоемкость, коэффициент Пуассона

Количество теплоты , необходимое для нагревания массы однородного вещества от температурыдо температуры, пропорционально массе вещества и изменению температуры

, (5.1)

где - удельная теплоемкость вещества. Из формулы (5.1) следует

. (5.2)

Отсюда видно, что удельной теплоемкостью называют количество теплоты, необходимое для нагревания вещества массой 1 кг на 1 К.

Молярной теплоемкостью называют количество теплоты, необходимое для нагревания 1 моля вещества на 1 К

,

где - количество молей вещества,- молярная масса вещества. Из определения удельной теплоемкости следует, что она связана с молярной теплоемкостью соотношением

. (5.3)

Состояние газа может быть охарактеризовано тремя величинами – давлением , объемоми температурой. Уравнение, связывающее эти величины, называют уравнениемсостояния вещества. Для идеального газа уравнением состояния является уравнение Менделеева-Клайперона, которое имеет вид

, (5.4)

где - универсальная газовая постоянная.

Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись уравнением состояния (5.4) и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты , переданное системе, затрачивается на увеличение ее внутренней энергиии на работу, совершаемую системой против внешних сил

(5.5)

Воспользовавшись определением молярной теплоемкости, получим

(5.6)

Из формулы (6.6) видно, что теплоемкость может иметь различные значения в зависимости от способа нагревания газа, так как одному и тому же значению могут соответствовать различные значенияи.

Внутренняя энергия идеального газа – это энергия теплового движения молекул и атомов в молекулах. Она складывается из кинетических энергий поступательного и вращательного движения молекул и энергии колебаний атомов в них. Согласно закону равнораспределения энергии по степеням свободы молекулы, на каждую поступательную и вращательную степень свободы молекулы приходится в среднем энергия, равная , гдеk – постоянная Больцмана, а на каждую колебательную степень свободы – энергия, равная kT. Таким образом, средняя энергия теплового движения молекулы идеального газа равна

,

где - число степеней свободы молекулы.Числом степеней свободы молекулы называют число независимых координат, определяющих положение молекулы в пространстве.

Внутренняя энергия  молей газа равна

.

Отсюда следует, что внутренняя энергия данного количества идеального газа зависит от его абсолютной температуры, но не зависит от объема, что является следствием модели идеального газа, в которой потенциальной энергией межмолекулярного взаимодействия пренебрегают.

Изменение внутренней энергии газа определяется формулой

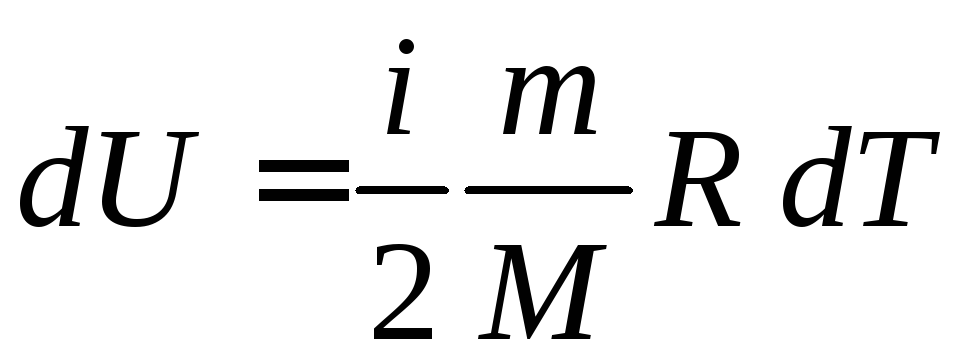. (5.7)

Рассмотрим основные процессы, протекающие в идеальном газе:

1. Изохорический процесс. Процесс называется изохорическим, если объем газа при изменении температуры остается неизменным. В этом случае =0, а следовательно=0 (элементарная работа газа=р), то есть вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (5.6) следует, что молярная теплоемкость газа при постоянном объеме равна

. (5.8)

2. Изобарический процесс. Процесс, протекающий при постоянном давлении, называется изобарическим. Для этого случая формула (5.6) перепишется в виде

. (5.9)

Используя уравнение состояния (5.4) получаем:

(5.10)

Но , следовательно,=0, поэтому. Подставляя это выражение в уравнение (5.9) получим

. (5.11)

Сравнивая уравнения (5.8) и (5.11) видим, что

. (5.12)

Уравнение (5.12) называется уравнением Майера.

3. Изотермический процесс. Изотермическим процессом называется процесс, протекающий при постоянной температуре. В этом случае =0 и, то есть внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу.

4. Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим. Первое начало термодинамики для такого процесса будет иметь вид

, или ,

то есть при адиабатическом процессе расширения или сжатия, работа совершается газом только за счет изменения запаса внутренней энергии.

Выведем уравнение адиабатического процесса. При адиабатическом расширении работа совершается за счет убыли внутренней энергии . Так каки, то

.

Разделив уравнение (5.10) на последнее уравнение и учитывая (5.12), получим

,

,

где - показатель адиабаты.

Интегрируя и потенцируя последнее уравнение, получим уравнение Пуассона

. (5.13)

Согласно кинетической теории газов,

. (5.14)

Эта формула справедлива как для молярных, так и для удельных теплоемкостей газов.