Глава 5. Модуляционные преобразования сигналов в системах электросвязи

5.1. Амплитудная модуляция

Передача сигналов в пространстве осуществляется с помощью «направляющих» объектов и сред. В системах электросвязи такими объектами и средами являются проводные (медные, оптические) линии передач, пространство радиоэфира и т.п. В рамках направляющих сред образуют различные каналы передачи сигналов. Полоса частот первичных сигналов, как правило, расположена в нижней части частотного спектра, а полосы частот каналов могут иметь самое разнообразное распределение по интервалам от очень низких, до гипервысоких частот. Другими словами, диапазон частот первичных сигналов и каналов их передачи несогласованны. При этом эффективно передаваемая полоса частот многих каналов (особенно широкополосных) намного шире полосы частот первичных сигналов, что позволяет передавать множество сигналов в одном канале. Следовательно, для передачи первичных сигналов возникает необходимость в их преобразовании:

1. Для осуществления переноса (трансформации) спектра первичных сигналов в эффективно передаваемую полосу частот каналов.

2. Для трансформации спектра первичных сигналов в заданный частотный интервал широкополосных каналов с целью уплотнения каналов в многоканальных системах.

В процессе переноса спектра первичных сигналов применяют дополнительный сигнал несущее гармоническое колебание. Несущее колебание должно быть согласованно по частоте с каналом передачи, т.е. должно быть в интервале эффективно передаваемой полосы частот канала передачи. В процессе трансформации спектра первичный сигнал как бы «нанизывается» на несущее колебание, наделяя несущее колебание своими признаками и становясь при этом переносчиком абонентского сообщения.

Процесс преобразования первичного сигнала с помощью изменения его одного (или нескольких) параметров несущего колебания (переносчика) по закону первичного сигнала называется модуляцией.

Различают непрерывную и импульсную модуляции. К непрерывной модуляции относят амплитудную и угловую модуляции. Рассмотрим подробнее амплитудную модуляцию первичного сигнала.

Используем в качестве переносчика сообщений (несущее колебание) гармонический сигнал

,

где соответственно амплитуда и частота несущего колебания.

Изменяя амплитуду несущего колебания по закону первичного сигнала, получим сигналамплитудной модуляции (АМ). Математическая модель амплитудно-модулированного сигнала представляется выражением

, (5.1)

где огибающая (амплитуда) АМ сигнала, являющаяся функцией первичного сигнала;коэффициент передачи модулятора (крутизна выходной характеристики модулятора). Формулу (5.1) ещё представляют в форме

, (5.2)

где коэффициент глубины АМ;модуль максимальной величины первичного сигнала. Величина коэффициента модуляции влияет на искажение первичного сигнала при модуляции. На практике, для избегания «перемодуляции» и, следовательно, нелинейных искажений первичного сигнала, величинувыбирают не более 0,50,7. На рисунке 5.1 приведёна временная диаграмма при АМ.

Формулы (5.1)-(3.2) описывают АМ с неподавленной несущей. Более эффективной (с точки зрения затрат энергии на перенос единицы абонентской информации) является балансная амплитудная модуляция (БАМ), Модель БАМ можно описать формулой

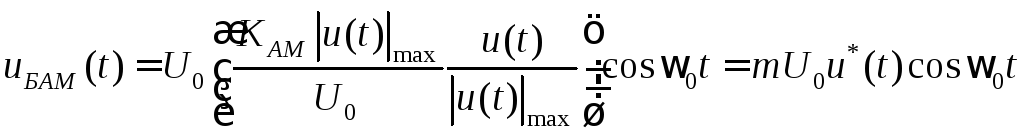, (5.3)

где девиация (максимальное отклонение) амплитуды в ходе модуляции. БАМ обеспечивает подавление (в реальности частичное подавление) несущего колебания. Чтобы понять это, рассмотрим спектральный состав АМ- и БАМ-сигналов.

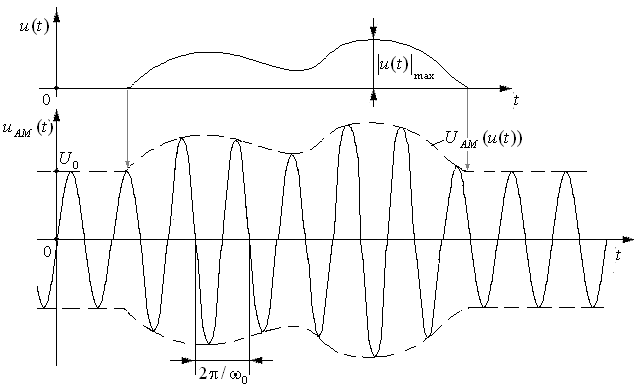
Рис. 5.1. Временные диаграммы при амплитудной модуляции

В качестве первичного сигнала возьмём гармонический сигнал тональной частоты (тональная частота). АМ сигнал тональной частоты согласно (5.2) равен

, (5.4)

где и. Применяя формулу Эйлера для функции, выражение (5.4) перепишем в виде

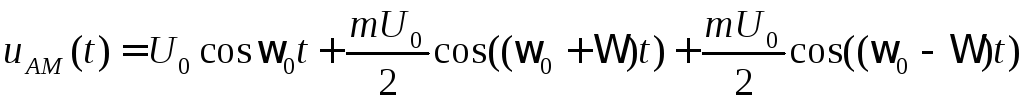. (5.5)

Формулу (5.5) легко получить также, используя известную в тригонометрии формулу произведения косинусов .

Из (5.5) видно, что спектральный состав включает компоненты на частоте несущей () и на боковых частотах: верхней () и нижней (). Аналогично, подставив выражение для первичного сигнала тональной частоты в (5.2), можно получить амплитудный спектр БАМ. Он будет отличаться от АМ отсутствием, но при этом верхний и нижний боковые лепестки спектра останутся. Линейчатые амплитудные спектры первичного, АМ и БАМ сигналов частоты даны на рисунке 5.2. Амплитудный спектр модулированного сигнала получается из спектра первичного сигнала путем переноса начала координат в точку, и симметричным расположением относительно этой точки боковых лепестков с изменением амплитуды враз.

Рис. 5.2. Амплитудные спектры первичного, АМ-, БАМ

сигнала тональной частоты

Рассмотрим АМ модуляцию более сложного первичного сигнала, представленного усечённым рядом Фурье (см. также параграф 3.1)

,

где соответственно амплитудный и фазовый спектр;период повторения первичного сигнала. Полагая, что-аягармоника разложения первичного сигнала максимальна, т.е., и, получим формулу АМ-сигнала в виде

(5.6)

где отношение-й гармоники к максимальной.

Амплитудный спектр модулированного периодического сигнала включает совокупность составляющих на основной частоте и боковых лепестках. При этом спектр боковых лепестков состоит из гармоник на частотах и() с амплитудами.

В качестве иллюстрации на рисунке 5.3 приведён амплитудный спектр АМ периодической последовательности импульсов. Спектр импульсной последовательности до модуляции изображён на рисунке 3.5 (см. также главу 3). Спектр АМ сигнала импульсной последовательности линейчатый, с интервалом между линиями рад/сек. Он зеркально симметричен относительно точки. Прилинейчатый спектр становится непрерывным (на рисунке 5.3 он обозначен пунктирной линией).

Рис. 5.3. Амплитудный спектр АМ импульсных сигналов,

Проведём частотный анализ балансной амплитудной модуляции для общего случая. Пусть первичный сигнал является непериодическим узкополосным квазигармоническим (т.е. «почти» гармонического) сигналом. Исходный сигналхарактеризуется комплексной спектральной характеристикой(определяемой по формуле (3.7) параграфа 3.1), АЧХ которого имеет верхнюю границу() (рисунок 5.4).

Для дальнейших рассуждений вместо сигнала удобно рассматривать его комплексные представления

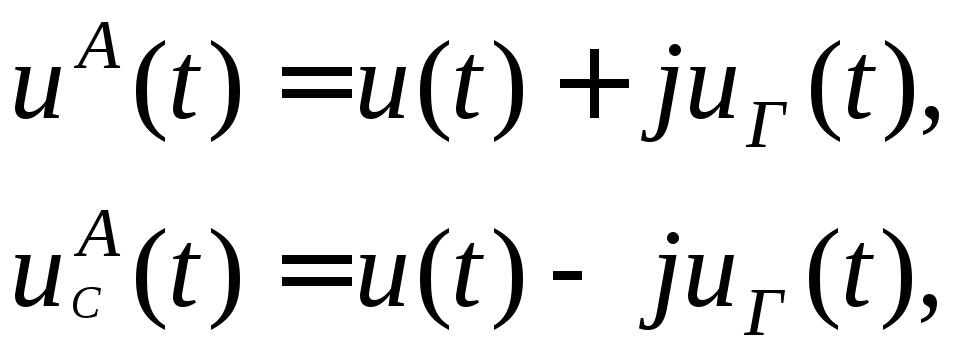(5.7)

где соответственно аналитический сигнал и его комплексное сопряжёние;сигнал, сопряжённый спо Гильберту (сопряжённым по Гильберту называется такой сигнал, у которого все гармонические составляющие спектра имеют такие же амплитуды, как у исходного сигнала, но при этом фазы смещены на угол). Выражения (5.7) обуславливают неоднозначность описания гармонических (квазигармонических) сигналов, которые можно представлять как функцией, так и сопряжённой ей функцией.

Сигналы характеризуются комплексными спектральными характеристиками соответственно, которые связаны ссоотношениями

(5.8)

(5.9)

В формулах (5.8) и (5.9) также учитывается ограничение спектра по частоте.

Формулы (5.9), (5.10) нетрудно получить, применив к (5.7) преобразование Фурье, и воспользовавшись соотношением (связывающим спектральные характеристики исходного и гильберто-сопряжённогосигналов)

,

где знаковая функция (, если, и, если).

Согласно формулам (5.8), (5.9) спектр исходного сигнала можно рассматривать как на положительных, так и на отрицательных частотах (см. рисунок 5.4).

Суммируя выражения (5.7), получим

.

Воспользуемся выражением (5.3)

. (5.11)

По формуле прямого преобразования Фурье (3.7) найдем спектральную характеристику БАМ сигнала

. (5.12)

Рис. 5.4. АЧХ исходного (первичного) и БАМ сигналов.

Из (5.12) можно увидеть, что в результате БАМ спектр соответствующих аналитических сигналов смещаются на величину , как в область положительных, так и отрицательных частот (на рисунке 5.4 показана трансформация спектра и его элементарного участка только в область положительных частот). При этом согласно (5.8),(5.9) в области положительных частот имеем

(5.13)

и в области отрицательных частот

Для положительных частот (имеющих смысл практического применения) уравнение (5.12) примет окончательный вид

или . (5.14)

Следовательно, спектральная плотность амплитуд БАМ (АМ) сигнала повторяет (копирует) форму аналогичного спектра исходного (первичного) сигнала. Спектр БАМ является результатом смещения спектра первичного сигнала из точки 0 в точку (см. рисунок 5.4). При этом интенсивность боковых полос модулированного сигнала меньше исходного враз. Ширина спектра АМ (БАМ) сигнала равна:.

Средняя плотность мощности АМ сигнала =на эквивалентном сопротивлении в 1[Ом], соответствующая элементарному участку спектра наодной боковой полосе, будет определяться как

,

где приращение амплитуды гармоник первичного сигнала, измеренная в единицах напряжения или тока (см. параграф 3.1) . Спектральная плотность мощностина одной боковой полосе равна

, (5.15)

где спектральная плотность мощности первичного сигнала. Из (5.15) видно, что спектральная плотность мощности (энергетический спектр) АМ (БАМ) сигнала такжеповторяет форму энергетического спектра исходного (первичного) сигнала, смещённого из точки 0 в точку (см. рисунок 5.4). При этом энергия боковых полос модулированного сигнала меньше исходного враз. Эффективная ширина энергетического спектра не изменяется.

Полная мощность модулированного сигнала определяется выражением

,

где мощность несущего колебания (для БАМ).

В качестве ещё одной иллюстрации на рисунке 5.5 приведёны спектральные плотности мощности ислучайного телеграфного сигнала (см. параграф 3.1), на этом же рисункеэффективная полоса пропускания модулированного сигнала.

Рис. 5.5. Спектральная плотность мощности

первичного и БАМ сигналов