Глава 3. Математические модели, характеристки и параметры сигналов электросвязи

3.1. Модели детерминированных сигналов электросвязи

В системах многоканальной связи первичные сигналы представляются электрическими колебаниями (напряжения, тока), изменяющимися во времени. При этом используемые физические процессы не доступны органам чувств человека и требуют специальных средств измерений. Сигналы в каналах связи подвергаются различным изменениям, искажениям. С целью анализа передачи сигналов по каналам связи необходимо изучать модели и методы их описания. Математические модели и характеристики сигналов является фундаментом понимания процессов передачи сигналов в технике многоканальной связи.

3.1.1. Модели описания сигналов функциональными методами. Сигналы изменяются с течением времени, поэтому удобной формой представления сигналов является функция времени . Она устанавливает связь между значениями электрических параметров сигналови временем. Сигналы электросвязи могут быть детерминированными (регулярными) и случайными. Модель детерминированных сигналов представляется соответственно детерминированной функций. Для детерминированной функции её мгновенные значения однозначно предопределены заранее.

Самыми простейшими формами представления детерминированных функций являются табличное и графическое. Более сложным описанием является аналитическое представление, в котором записывается в виде формулы. Например, гармонические колебания (осцилляции) тока и напряжения можно представить аналитически в виде функций синуса и (или) косинуса. Так, модель гармонического сигнала в синусоидальной форме записи имеет вид

, (3.1)

где амплитуда сигнала (измеряется в таких же физических величинах, что и);угловая величина или аргумент функции синус (измеряется в радианах);постоянная Пифагора;циклическая частота (измеряется в рад/сек), циклическая частота есть мгновенная скорость изменения угловой величиныи является её производной по времени, т.е.:период повторения сигнала (измеряется в сек), величиначастота изменения сигнала, представляющая количество повторения формы сигнала в единицу времени (единица измерения - герц);начальная фаза колебания сигнала (измеряется в радианах),определяет момент запаздывания либо опережения сигнала,исвязаны формулой. Графическое изображение синусоидального колебания и его параметров приведено на рисунке 3.1.

Рис. 3.1. Графическое изображение гармонического

(синусоидального) колебания

Более сложные по форме сигналы можно описать во временной области методом аппроксимации. Суть аппроксимации заключается в замене некоторых участков временного тренда простыми (элементарными) функциями, например, линейными, гиперболическими, параболическими, экспоненциальными и т.п. На рисунке 3.2 приведён пример кусочно-линейной аппроксимации процесса сложной формы на временном интервале. В данном случае разобьём сигнална три временных участка,,. Каждый временной участок можно описать с помощью линейной функции (рисунок 3.2),

Аппроксимирующая модель исходного процессабудет выглядеть так

Рис.3.2. Пример кусочно-линейной аппроксимации сигнала

К недостаткам описания сигналов электросвязи во временной области можно отнести громоздкость записи, неоднозначность выбора функций аппроксимации, снижение точности описания реальных физических процессов.

3.1.2. Описание сигналов методами спектральной аппроксимации. Спектральные методы описания сигналов дают более универсальную модель представления процессов передачи сообщений.

Рассмотрим некоторый периодический (повторяющийся во времени) процесс, описываемый функцией . С математической точки зрения процесс называется периодическим, если он удовлетворяет равенству

, (3.2)

где период повторения (измеряется в сек);любое целое число, задающее кратность повторения сигнала.

Большинство периодических процессов в электросвязи можно разложить в тригонометрический ряд Фурье

. (3.3)

Общий смысл (3.3) означает, что многие периодические сигналы аппроксимируются гармоническими функциями синус и косинус, аргумент которых кратен основной частоте , определяемой периодом повторениясигнала. Иначе говоря, сигнальный процесс рассматривается как совокупность простейших колебаний (осцилляций), как некоторый аккорд, состоящий из отдельных нот, определяющие структуру процесса. В формуле (3.3)коэффициенты разложения (определяют амплитуду каждого синусоидального и косинусоидального колебаний, являющиеся спектром) определяются по формулам:

, . (3.4)

Коэффициент в формуле (3.3) определяет наличие постоянной (средней) составляющей ви вычисляется как

. (3.5)

Рассмотрим разложение в ряд Фурье периодической последовательности импульсов амплитудой, длительностьюи периодом(рисунок 3.3).В соответствии с формулами (3.4)

а) б)

Рис. 3.3. а) Периодическая последовательность импульсов,

б) Одиночный импульс

и рисунком 3.3 вычислим коэффициенты :

;

;

.

Коэффициенты разложения получены также из условия, что на временных участках(см. рисунок 3.3,а).

Модель , аппроксимирующая периодическую последовательность импульсовна рисунке 3.3, может быть представлена усечённым рядом Фурье ():

Функция является приближённой математической моделью исходного процесса(см. рисунок 3.3,а). Точность описания процесса(или ошибка аппроксимации) будет тем выше (меньше), чем больше слагаемых будет использоваться в усечённом ряде. То есть, если, то.

Следует отметить, что спектральное представление моделей сигналов в электросвязи не ограничивается только тригонометрическим рядом Фурье (3.3). Вместо функций синуса и косинуса в (3.3) могут быть использованы и другие базисные функции разложения, например, с помощью ортонормированных нестационарных полиномов Лежандра, различных вейвлет-функций и др. В этом случае аппроксимацию временных процессов осуществляют обобщённым рядом Фурье. Вопрос о применении нетригонометрических функций в обобщённом ряде Фурье диктуется характером решаемых задач и свойством анализируемых сигналов.

Дальнейшим развитием метода гармонической аппроксимации сигналов (3.3) является описание сигнала в форме интеграла Фурье, комплексная форма которого имеет вид

, (3.6)

где некоторая переменная размерности циклической частоты, являющаяся переменной интегрирования;переменная интегрирования размерности времени;мнимая единица. Формула (3.6) является результатом предельного перехода разложения периодической функции в ряд Фурье (3.3), если период повторенияфункции увеличить до бесконечности. Математическая форма (3.6) позволяет производить частотный анализ (его физический смысл рассматривается ниже) непериодических сигналов. В этом случае непериодические сигналы условно полагают периодическими, период повторения которых надо «ожидать» бесконечно долго.

Интеграл Фурье (3.6) часто представляют в виде двух формул. Для этого вводят в рассмотрение комплексную спектральную характеристику , которую вычисляют как

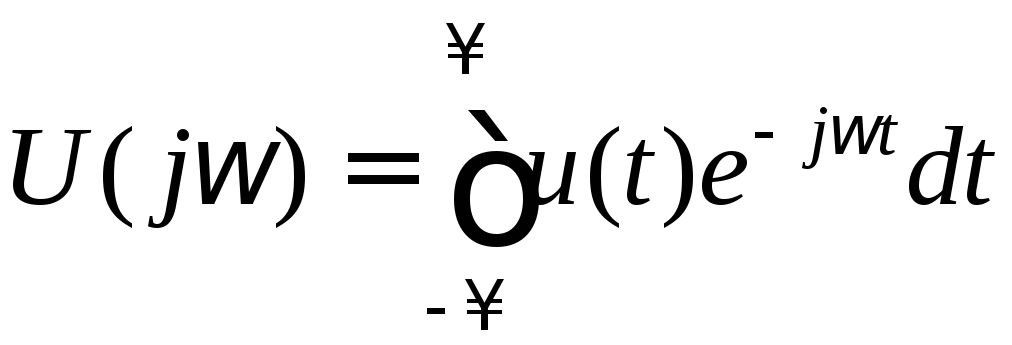. (3.7)

Тогда (3.6) перепишется в виде

. (3.8)

Формулу (3.7) называют прямым преобразованием Фурье функции , а формулу (3.8)обратным преобразованием Фурье.

Подчеркнём, что прямое и обратное преобразование Фурье, а также ряд Фурье имеют важное фундаментальное значение в гармоническом анализе физических процессов в технике связи и во многих других областях знаний.

В качестве иллюстрации рассмотрим пример прямого преобразования Фурье экспоненциальной функции:

(3.9)

Согласно (3.6) комплексная спектральная характеристика равна

. (3.10)

Естественно предположить, что обратное преобразование комплексной функции даёт(для). На самом деле, подставляяв (3.8), получим решение

,

где вычет подынтегральной функции;особая точка комплексной функции(в рассматриваемом примереполюс, значение получается из решения уравнения). Тогда в соответствии с правилами вычисления вычета однократного полюса комплексной подынтегральной функции имеем

3.1.3 Модели описания сигналов на основе частотного представления. Описание сигналов на основе частотного представления является логическим следствием методов спектрального гармонического анализа. Ряд Фурье (3.3) для периодического сигнала с периодом повторенияс помощью тригонометрических преобразований можно упростить до вида

, (3.11)

где ,(3.12)

называют соответственно амплитудным и фазовым частотным спектром периодического сигнала; при этом и. В отличие от (3.3) в разложении (3.11) используется только один тип функцийкосинус, амплитудаи фазовый аргументкоторых зависит от номерагармоники как независимой переменной. Так как, то амплитудный и фазовый частотный спектр удобно графически изобразить в виде диаграммы отрезков (спектральных линий) длины,, проведённых перпендикулярно оси, на которую наносятся значенияили. При этом частотный спектр периодических сигналов имеет дискретный (разрывный) характер, его ещё называют линейчатым. Расстояние между отдельными спектральными линиями в общем случае будет равно.

Построим амплитудно-фазовый частотный спектр функции , модель которого представлена функцией синус. Для этого перепишем (3.1) в виде

.

Амплитудный частотный спектр гармонической функции (3.1) приведён на рисунке 3.4 выше оси , фазовый частотный спектр – дляниже. Её амплитудный частотный спектр представляет линию высотой, проведённую на оси частот в точке. Линия высотойв точке(см. рисунок 3.4) является фазовым спектром гармонического сигнала (3.1).

Рис.3.4. Линейчатый частотный спектр гармонической функции

Рассмотрим ещё один пример получения частотных спектров для периодической последовательности импульсов (рисунок 3.3,а). Спектры импульсов получим на основе формул (3.12) и коэффициентов разложения в ряд Фурье:

; (3.13)

.

Линейчатый амплитудный частотный спектр периодических импульсов изображён на рисунке 3.5. Он представлен набором линий, проведённых через точки кратных основной частоте , и имеют также спектральную линию в точке, что говорит о наличии постоянной составляющей в однополярной последовательности импульсов (см. рисунок 3.3,а). При этом фазовый частотный спектр последовательности импульсов равен нулю во всех точках разложения, его график не приводится.

Подчеркнём, что между периодическими функциями и их частотными спектрами существует взаимно-однозначное соответствие: периодическая функция полностью определяет её частотные спектры, и наоборот, зная частотные спектры, можно указать какой периодической функции они принадлежат. Благодаря этому в ряде задач электросвязи оказывается удобным операции над периодическими процессами заменять операциями над частотными спектрами, характеризующие эти процессы.

Рис. 3.5. Линейчатый амплитудный частотный спектр периодической последовательности импульсов

При увеличении периода повторения сигнала, величинауменьшается, соответственно уменьшается расстояние между линиями линейчатого спектра. В пределе, при увеличениидо бесконечности (), длина отрезка между смежными спектральными линиями уменьшается до нуля, линии как бы «смыкаются». Вместе они образуют непрерывный частотный спектр, на рисунке 3.5 огибающая линия непрерывного спектра обозначена пунктирной линией. Непрерывный частотный спектр соответствует одиночному импульсу длительности, который изображён на рисунке 3.3,б.

Модель непрерывного частотного спектра амплитуд одиночного импульса может быть получена из формулы (3.13). Перепишем (3.13) в виде

.

Далее, устремляя , дискретная переменнаябудет превращаться в непрерывную переменную(имеющей размерность циклической частоты), ибудет функцией от, которую обозначим как. Тогда формулу дляможно переписать следующим образом

. (3.14)

Подчеркнём, что описывает огибающую амплитудного спектра одиночного импульса, который по мере того, как, становится непериодическим сигналом (см. рисунок 3.3,б). Существенное «физическое» отличиеоттакже заключается в том, чтохарактеризует распределение относительных амплитуд гармоник разложения (в знаменателе формулы 3.14 присутствует), тогда какхарактеризует распределение абсолютных значений амплитуды-й гармоники разложения с частотой. Другими словами,есть спектральная плотность амплитуд, т.е. средняя величина амплитуд гармоник, приходящая на единицу длины частотного интервала. При этомизмеряется в физических единицах (как) приведённых к рад/сек, тогда какизмеряется в тех же физических единицах, что и сам сигнал.

Частотные спектральные характеристики непериодических сигналов могут быть получены напрямую с помощью комплексной функции, являющейся результатом Фурье преобразованием сигнала(см. (3.7)). На основе формул Эйлера () и чётности функции косинус () перепишем (3.7) в виде

, (3.15)

где соответственно веществен- ная и мнимая части комплексной спектральной характеристики. Функциютакже можно представить в показательной форме

, (3.16)

где амплитудно-частотная характеристика (АЧХ) непериодического сигнала;фазо-частотная характеристика (ФЧХ) непериодического сигнала. АЧХ отражает закон распределения плотности амплитуд гармоник разложения сигналаот частоты, ФЧХзакон распределения начальной фазы гармоник этого разложения от. Так как частотапринимает непрерывный ряд значений, то графики функцийописываются непрерывными линиями.

Построим АЧХ и ФЧХ комплексной функции примера (3.10). Разложимна вещественную и мнимую составляющие

,

где .

Тогда и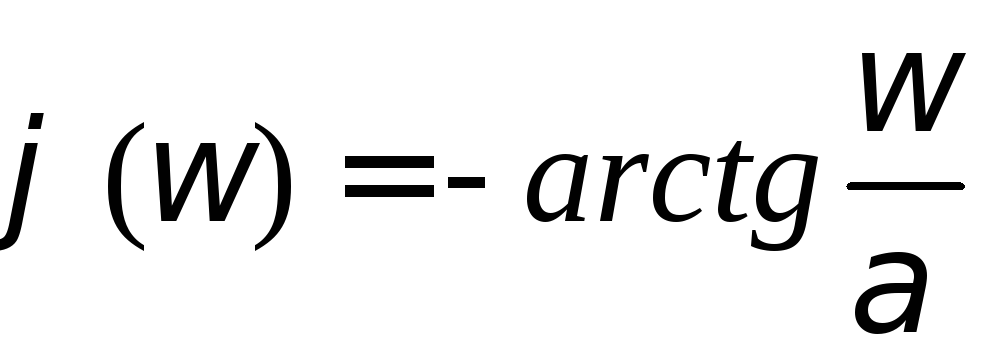, графики которых изображены на рисунке 3.6.

Рис. 3.6. АЧХ и ФЧХ экспоненциального сигнала

Следует отметить, что для непериодического сигнала абсолютная величина амплитуды гармоник разложения равна нулю. Для практических целей вводят понятие приращения амплитуды гармоникразложения непериодического сигнала, которая вычисляется по формуле (она выводится из (3.8))

. (3.17)

Величина пропорциональна площади фигуры, приведённой на рисунке 3.6.