6.2. Линейное разделение сигналов. Oртогональные переносчики

Увеличение числа уплотняемых каналов без увеличения числа физических линий возможно путём наделения сигналов особыми индивидуальными признаками, которые бы приводили к различению уплотняемых каналов с целью их дальнейшего разделения. Такими признаками в обще случае могут быть параметры переносчиков сигналов: амплитуда, частота, фаза в случае непрерывной модуляции, временное положение, длительность или форма импульсов при дискретной модуляции.

Пусть необходимо организовать одновременную и независимую работу индивидуальных каналов по общему групповому тракту. Предположим, что каждый канал есть результат я балансной амплитудной или узкополосной угловой модуляции первичного сигнала, линеаризованная модель которых в упрощённой форме имеет вид

, (6.5)

где соответственно первичный сигнал и функция переносчика-го канала,.

Будем также полагать, что сумма верхних границ эффективно передаваемых участков спектра первичных сигналов намного меньше частотыканальных переносчиков, т.е.

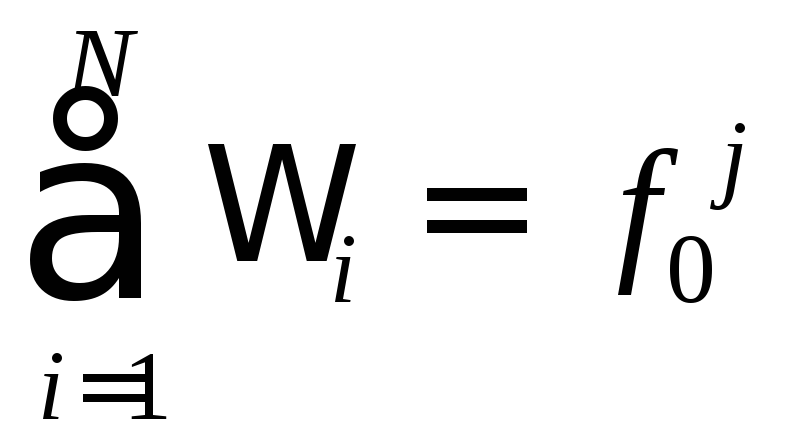для всех . (6.6)

Сигнал группового тракта в соответствии с формулами (6.5) и (6.2) равен

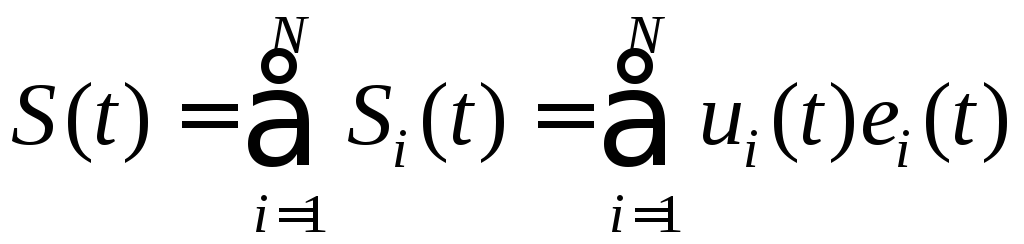. (6.7)

Функцию модели группового сигнала можно увязать с фильтрующими свойствами дельта-функции (см. также формулу (4.9) третьей главы), а именно

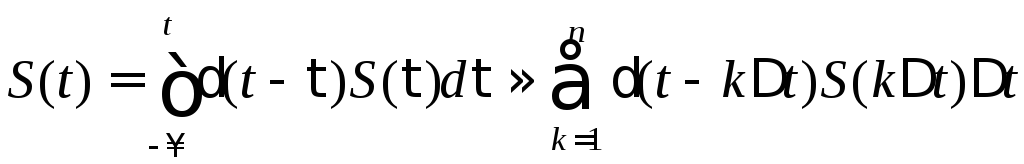, (6.8)

где дельта-функция;-ый дискретный отсчёт сигнала;время дискретизации.

Согласно (6.7) подставим в (6.8) значения канальных сигналов , взятые в отсчётные моменты времени,

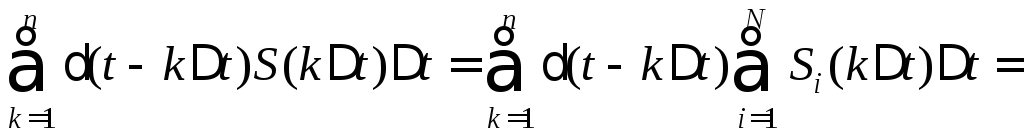
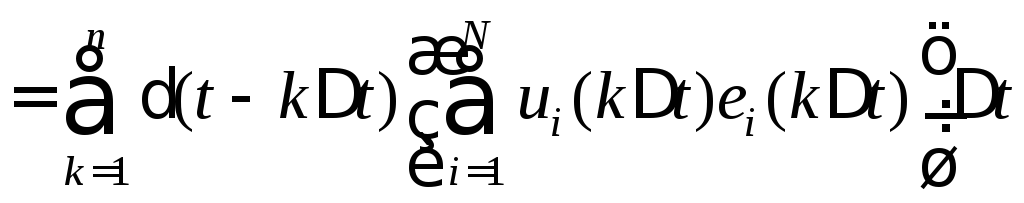. (6.9)

Если считать, что в канале передачи отсутствуют искажения и помехи, то оценка группового сигнала (см. рисунок 6.1) равна сигналу.

На приёмной стороне системы будем наблюдать за сигналом в течение короткого промежутка времени, также для удобства возьмём. Так как интервалотносительно короткий, то согласно (6.6) изменение сигналов,будет обусловлено действием только одних переносчиков, а не первичных сигналов. Тогда можно положить, что значения первичного сигнала являются константами для выбранного промежутка времени наблюдения, т.е.

, . (6.10)

Нетрудно видеть, что условие (6.9) будет выполняться, если будут соблюдаться система равенств по отдельным отсчётам группового сигнала:

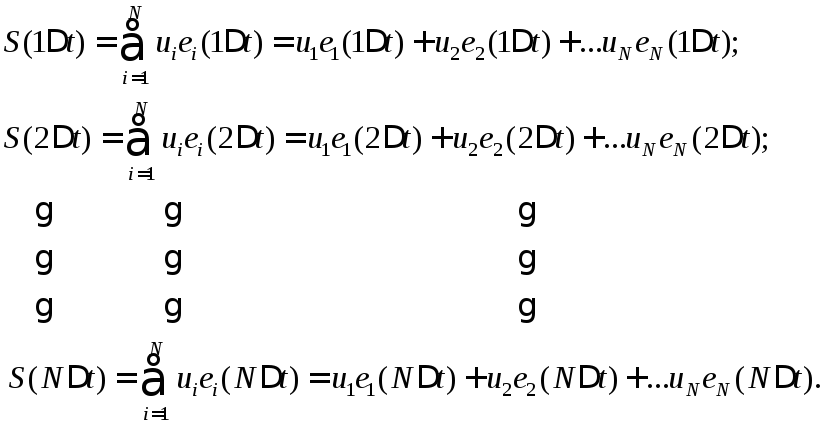(6.11)

Система (6.11) получена с учётом (6.10).

Выражение (6.11) может быть переписано в компактной матричной форме. Введем в рассмотрение вспомогательный вектор отсчётов группового сигнала, вектор первичных сигналови матрицу переносчиков:

.

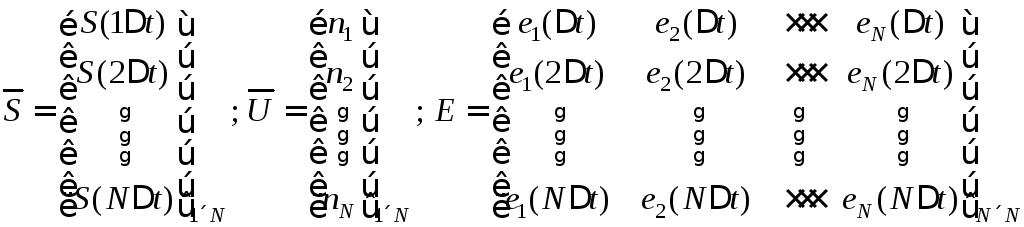С учётом введенных обозначений система (6.11) будет описываться так

. (6.12)

Так как передача группового сигнала происходит без искажения, то выделение первичных сигналов осуществляется по данным отсчётов группового сигнала. При этом признаки канальных сигналов определяются матрицей переносчиков, которая должна быть «известной» для аппаратуры разделения каналов в приёмной части многоканальной системы. Другими словами, задача разделения каналов сводится к определению вектора отсчётных значений первичных сигналовпри условии, что известными являются вектор наблюдения группового сигналаи матрица переносчиков. Следовательно, чтобы определить векторнадо решить систему линейных уравнений (6.12). Решение (6.12) можно записать в виде

, (6.13)

где матрица обратная;единичная матрица размерности. Как видно из (6.13), решение системы линейных уравнений (6.12) связано с обращением квадратной матрицы переносчиков.

Из курса линейной алгебры известно, что обращение квадратной матрицы связано с вычислением её определителя. Обозначим определитель матрицы как. Также из теории решения линейных уравнений известно, что единственность (однозначность) решения (6.13) возможно, если

. (6.14)

Ненулевое значение определителя (6.14) возможно тогда и только тогда, когда столбцы (и строки) матрицы линейно независимы. Условие линейной независимости столбцов формулируется так: взвешенная сумма столбцов матрицыравна нулевому вектору, т.е.

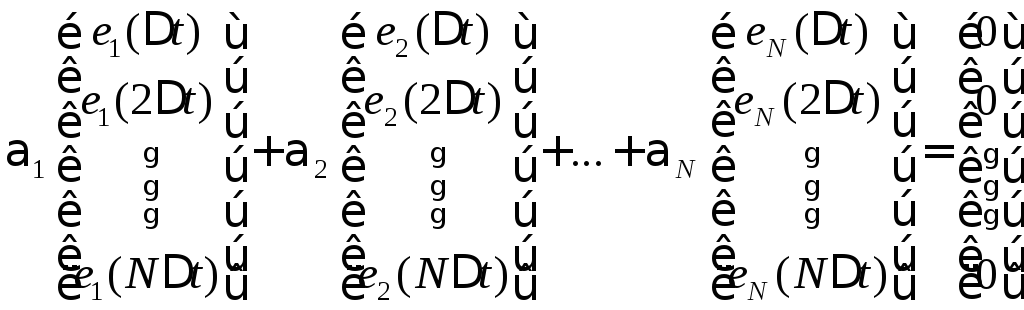, (6.15)

только тогда, когда числа . Если найдётся хотя бы одно число, то определитель (6.14) будет равен нулю и система (6.12) не будет иметь единственного и однозначного решения, что говорит невозможности разделения каналов на приёмной стороне многоканальной системы.

Каждый столбец представлен в (6.15) отсчётами переносчиков -го канала. Следовательно, первое условие построения многоканальных систем связи заключается в обеспечениилинейной независимости переносчиков канальных сигналов.

Переносчики сигналов могут быть представлены непрерывными функциями времени (). В общем случае условие линейной независимости переносчиков канальных сигналов записывается в виде

только когда для некоторого временного интервала, в течение которого осуществляется многоканальная передача сигналов.

Например, гармонические переносчики вида () являются линейно независимыми, если будут иметь разные частотыдля каждого канала. В противном случае они будут линейно зависимыми, даже, если будут характеризоваться разными значениями амплитуд.

Как видно из формулы (6.13) для того, чтобы восстановить вектор первичного сигнала необходимо произвести обращение матрицы, что является достаточно трудоёмкой операцией, которая усложняется при увеличенииколичества каналов.

Решение уравнения (6.12) существенно упрощается, если матрица E является ортогональной, т.е. её обратная матрица равняется транспонированной матрице

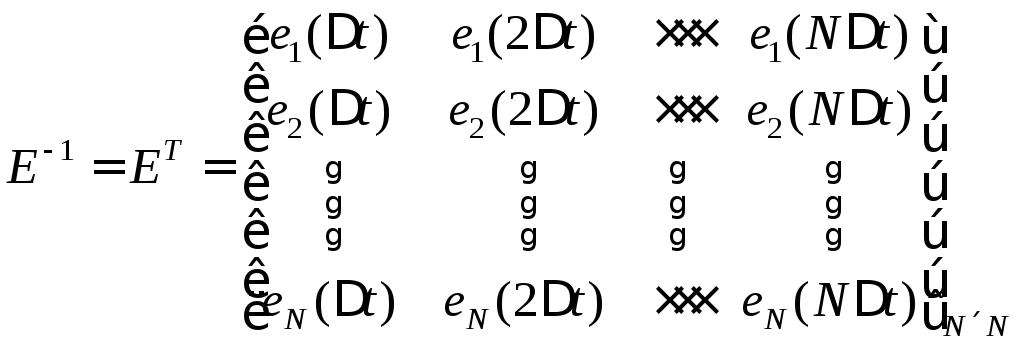
и . (6.16)

Выпишем подробнее произведение матриц и приравняем его единичной матрице:

.

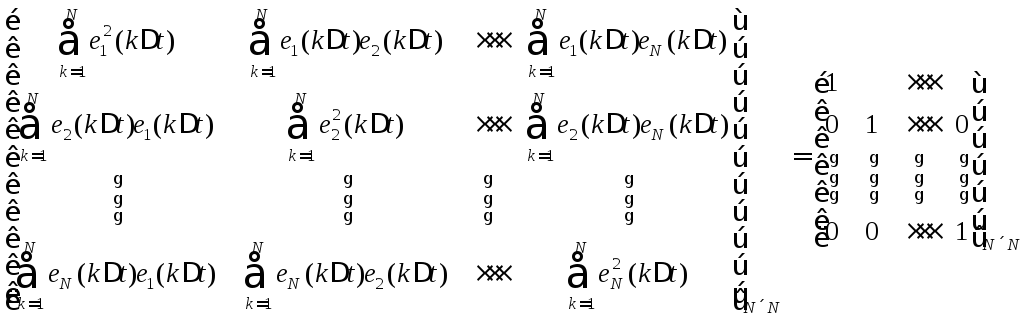Из последнего равенства нетрудно установить новое свойство переносчиков: сумма произведения дискретных отсчётов «одноимённых» (с одним и тем же индексом одним и тем же номером канала) переносчиков не равна нулю, а «разноимённых» (для разных индексовразных каналов)равна нулю, т.е.

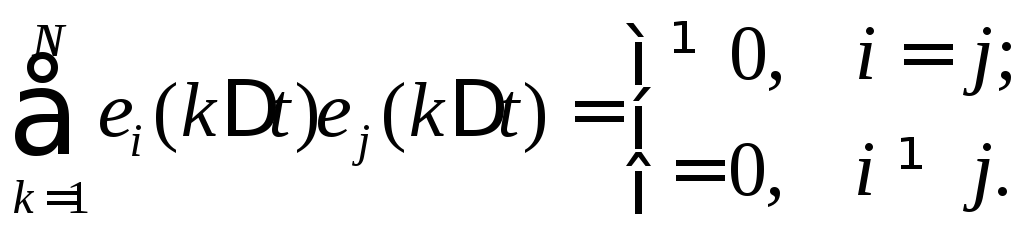(6.17)

Свойство (6.17) определяет ортогональность переносчиков «разноимённых» канальных сигналов.

По существу левая часть выражения (6.17) в -мерном пространстве Евклида есть скалярное произведение векторови, т.е.

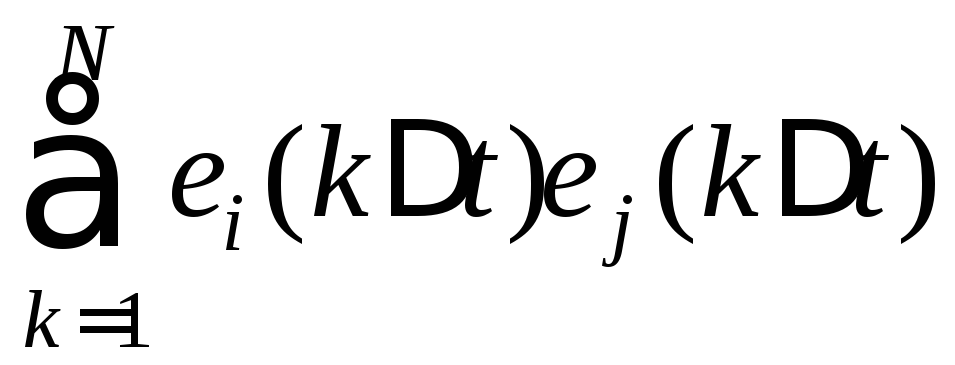, (6.18)

где индекс транспонирования. Скалярное произведение отражает проекцию векторов друг на друга. Так, есливекторыиортогональны, то их взаимная проекция равна нулю. Если, то сумма (6.17) и (6.18) равна квадрату длины (нормы) вектора.

Следует заметить, что если переносчики сигналов ортогональны, то решение линейной системы уравнений (6.12) резко упрощается

и (6.19)

В общем случае, при пространство Евклида переходит в бесконечномерное пространство Гильберта. В этом случае скалярное произведение отсчётов (6.17) заменяется скалярным произведением непрерывных функций переносчиков. Для вещественных функций переносчиковипринцип ортогональности на конечном временном интервале наблюденияпримет вид

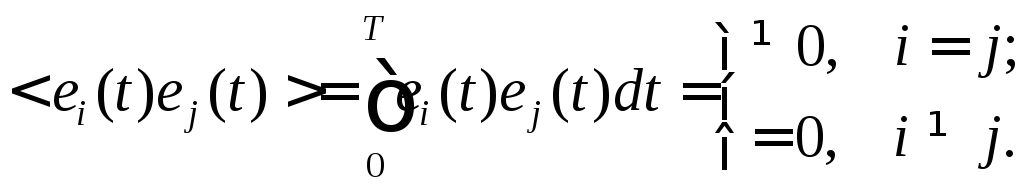. (6.20)

Для бесконечного интервала наблюдения ортогональность непрерывных переносчиков будет иметь вид

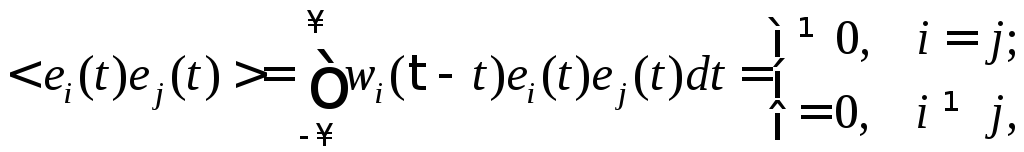(6.21)

где некоторая весовая функция (смысл её поясняется ниже).

Представленные основы теории линейного разделения каналов были построены без учёта действия помех и искажений в каналах передачи. В этих условиях построение многоканальных систем может осуществляться без особой разницы, как из условия линейной независимости, так и условия ортогональности канальных переносчиков . Однако при наличии в каналах помех предпочтение отдаётся многоканальным системам с ортогональными переносчиками, позволяющими повысить помехоустойчивость передаваемых сигналов.