17

1.4. Система обозначений

Как известно, режим линейной электрической цепи, каковой и является схема замещения ЭЭС для расчета установившегося режима, полностью описывается уравнениями законов Ома и Кирхгофа. Однако для записи этих уравнений должны быть приняты определенные обозначения. Остановимся кратко на используемой далее системе обозначений.

Закон Ома устанавливает взаимосвязь параметров каждой из ветвей цепи. Будем считать, что положительные направления параметров режима некоторой

ветви приняты от ее условного начала n к условному концу к (рис.1.6).

Рис.1.6 Положительные направления параметров режима ветви

Тогда для ветви, характеризующейся сопротивлением z вi , действующей в ней ЭДС Е вi и протекающим по ней токомI вi , разность потенциалов между ее кон-

цами U вi ( падение напряжения на ветви) в соответствии с законом Ома будет определяться уравнением:

Рис.1.7 Ветви с взаимоиндуктивной связью.

18

поэтому, в предположении, что ЭДС самоиндукции и взаимоиндукции в ветвях i

ческой цепи и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю. Принимая в качестве положительного направления для токов, связанных с произвольным узлом, направление от узла (рис.1.8), уравнение первого закона Кирхгофа получим в виде:

Рис.1.8 Положительные направления токов в узле.

Второй закон Кирхгофа определяет баланс напряжений в замкнутых контурах электрической цепи и формулируется следующим образом: алгебраическая сумма падений напряжения на ветвях замкнутого контура равна нулю. Для произвольного контура, содержащего l ветвей (рис.1.9), уравнение второго закона Кирхгофа запишется в виде:

i =1

19

Обычно при составлении уравнений(1.6) падения напряжений ветвей, совпадающие с направлениям обхода контура учитываются в алгебраической сумме с положительными знаками, а несовпадающие – с отрицательными.

U в1

U в2

U в3

Рис.1.9 Положительные направления напряжений в замкнутом контуре

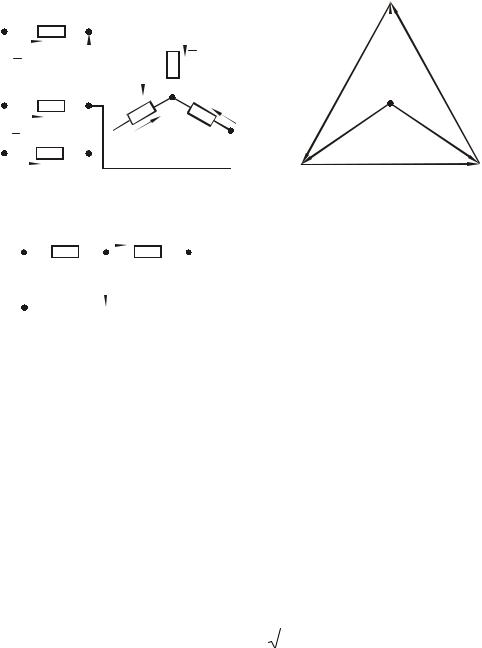
Несмотря на то, что расчеты установившихся режимов работы трехфазных ЭЭС чаще всего выполняются с помощью схем замещения, составленных для одной фазы, характеристику этих режимов принято осуществлять с помощью параметров режимов, свойственных трехфазным системам: комплексными величинами токов I А , I В и I С (рис.1.10), фазных напряжений - U А , U В , U С , определенных

относительно нейтрали или земли, междуфазных (линейных) напряжений - U АВ ,

U ВС и U СА .

Чаще всего однофазные схемы замещения составляются и рассчитываются для фазы А ЭЭС(рис.1.10, б), т. к. для трехфазной системы, обладающей циклической симметрией, при известных комплексах параметров режима фазы А параметры фаз В и С легко определяются с помощью коррекции фазовых углов векторов, отвечающих фазе А (рис.1.10, в).

б)

Рис.1.10 Пояснение к системе обозначения параметров режима трехфазной системы: а, б – трехфазная и однофазная схемы замещения; в – векторная диа-

грамма напряжений трехфазной симметричной системы.

Напомним, что номинальные напряжения электрических сетей – это междуфазные напряжения.

Комплексные сопротивления элементов схем замещения ЭЭС будем пред-

где x - применяется со знаком плюс для индуктивных элементов и со знаком минус – для емкостных.

Проводимости элементов будем представлять как:

где в также применяется со знаком плюс для индуктивных элементов и со знаком минус – для емкостных.

21

Соответственно комплексы рассмотренных выше напряжений можно пред-