103

5. МЕТОДЫ ОПТИМИЗАЦИИ РАСЧЕТОВ РЕЖИМОВ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ

Современные электроэнергетические системы содержат большое количество узлов, определяющее порядок системы уравнений при анализе режимов работы этих систем. Решение систем уравнений высокого порядка требует значительного времени и большого объема оперативной памяти ЭВМ, поэтому для повышения эффективности необходимо применять специальные методы повышения скорости расчетов и экономии оперативной памяти. В качестве таких методов можно рассмотреть эквивалентирование, разделение на подсистемы, учет слабой заполненности матриц коэффициентов уравнений состояния электрической сети и другие.

5.1. Приведение комплексных уравнений к системе действительных уравнений

Для цепи переменного тока узловые напряжения, токи в узлах, собственные и взаимные проводимости узлов являются комплексными величинами. В этом

случае систему уравнений узловых напряжений при равенстве нулю напряжения балансирующего узла можно записать в матричной форме в следующем виде:

При решении на ЭВМ уравнения узловых напряжений для сети переменного тока, как правило, приводятся к системе действительных уравнений порядка2n , где n - число независимых узлов. Для этого представляют матрицы с комплексными элементами в виде сумм матриц с действительными элементами, при этом нужно в виде такой суммы представить каждый комплексный элемент и учесть правило сложения матриц:

Произведя перемножение, запишем отдельно действительные и мнимые величины:

104

Таким образом, cистему уравнений узловых напряжений для цепи переменного тока можно записать в матричной форме в следующем виде:

Система (5.6) и является системой действительных уравнений порядка 2n и содержит 2n неизвестных активных и реактивных напряжений.

Эффект заключается в исключении операций с комплексными элементами.

5.2. Учет слабой заполненности матриц коэффициентов уравнений состояния при расчетах установившихся режимов

Эффективность расчетов можно существенно повысить, если учесть наличие и расположение нулевых элементов в матрице Yу . Эффект достигается за счет

того, что необходимо запоминать лишь ненулевые элементы, а также за счет исключения операций с нулевыми элементами. В результате экономится оперативная память ЭВМ и повышается скорость расчетов. Ни одна из современных программ расчета установившихся режимов, в которой реализован метод Гаусса(как наиболее удобный), не может быть эффективной, если в ней не предусмотрен учет слабой заполненности матриц коэффициентов уравнений состояния.

Фактически задача сводится к такой форме записи уравнений состояния, при которой ненулевые элементы матрицы узловых проводимостей будут сгруппированы таким образом, чтобы в ходе решения системы линейных уравнений методом Гаусса появилось как можно меньше новых ненулевых элементов. Такой эффект достигается, если матрица коэффициентов приведена к ленточной форме. Матрицей в ленточной форме называют такую, у которой ненулевые элементы расположены в виде “ленты” вдоль главной диагонали матрицы.

Расположение ненулевых элементов матрицы Yу определяется способом нумерации узлов электрической системы. Проиллюстрируем способ нумерации узлов на примере квадратной матрицы присоединений узлов, которая состоит из нулей и единиц. Если узел к соединен с узлом j (то есть Yку ¹ 0 ), то на пересе-

чении строки и столбца, соответствующих номерам узлов к и j стоит 1 (для учета слабой заполненности знак перед единицей значения не имеет). Естественно, диагональные элементы матрицы тоже равны единице. Таким образом, матрица присоединений отличается от матрицы узловых проводимостей тем, что все ненулевые элементы заменены единицами. На рис. 5.1 показана схема с произвольной нумерацией (рис.5.1, а) и соответствующая ей матрица присоединений (рис.5.1, б).

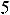
106

Первый номер присваивают узлу с минимальной степенью. Если таких узлов несколько, то выбирают любой из них. Присвоим первый номер узлу 2. Далее в порядке возрастания номеров уже пронумерованных узлов нумеруют смежные с ними непронумерованные узлы, причем нумерация ведется в порядке возрастания их степеней, как показано на рисунке 5.2, а, б и в табл. 5.1.

а) новая нумерация

б) матрица присоединений узлов в ленточной форме Рис.5.2

Как видно из рис. 5.2, б, ненулевые элементы матрицы присоединений сгруппированы в результате такой нумерации вдоль главной диагонали в виде “ленты”.

Этот способ нумерации, один из наиболее простых и эффективных при применении метода Гаусса, достаточно легко реализуется на ЭВМ.

5.3. Эквивалентирование в расчетах установившихся режимов электрических систем

Предположим, что необходимо проанализировать изменение режима при изменении нагрузки в нескольких близко расположенных узлах. Это изменение оказывает влияние не на всю электрическую систему изп узлов, а лишь на ее часть, из nII узлов, причем nII < n . Во многих случаях на основании опыта расчетов и анализа режимов электрической системы с той или иной степенью точности эту часть определить можно. Очевидно, что в рассматриваемом случае целесообразно заменить всю систему из n узлов на некоторую эквивалентную систему из nII узлов, содержащую только те узлы, для которых необходимо проанализировать изменения параметров режима. После этого нужно рассчитать установившийся режим только эквивалентной системы из nII узлов. Эффект от такого эквивалентирования заключается в уменьшении числа узлов анализируемой электрической системы и, следовательно, в понижении порядка матрицы коэффициентов уравнения состояния. Соответственно этому уменьшается объем требуемой оперативной памяти ЭВМ и время расчета, упрощается анализ режима электрической системы.

107

Схема считается эквивалентной, если в результате расчета ее режима определяются те же значения напряжений оставшихся в ней узлов, что и при расчете исходной системы, то есть до эквивалентирования. Остальные узлы исключаются, и напряжения в них не могут быть определены в результате расчета эквивалентной системы. Обычно при эквивалентировании предполагают, что в качестве активных элементов схема содержит только задающие токи, а все ЭДС ветвей предполагаются предварительно замененными эквивалентными задающими токами.

Рассмотрим эквивалентирование на примере матрицы узловых проводимостей. Число независимых узлов и порядок матрицы Yу равен n . В эквивалентной

системе содержится nII независимых узлов, а при эквивалентировании исключается nI узлов, причем

nI = n - nII .

Разобьем матрицу проводимостей и матрицы-столбцы узловых напряжений и задающих токов на блоки, соответствующие эквивалентной системе и исключенной части. Запишем уравнение узловых напряжений :

В этом уравнении YII-II - матрица собственных и взаимных проводимостей узлов эквивалентной системы; UII , I уII - матрицы-столбцы узловых напряжений и за-

дающих токов эквивалентной системы; YI-I , UI , I уI включают в себя узловые

проводимости, напряжения и задающие токи узлов исключаемой части системы. YI-II состоит из взаимных проводимостей узлов, входящих в эквивалентную и исключаемую системы. Это – проводимости ветвей, соединяющих узлы эквивалентной и исключаемой системы.

Произведем формальное перемножение матриц в выражении(5.7) и запишем результат в виде двух матричных уравнений:

Из первого уравнения системы (5.8) выразим напряжения исключаемых узлов через напряжения эквивалентной системы:

Подставив (5.9) во второе уравнение системы(5.8), получим уравнение узловых напряжений только для эквивалентной системы: