
- •1. УРАВНЕНИЯ УСТАНОВИВШИХСЯ РЕЖИМОВ РАБОТЫ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ
- •1.1. Некоторые сведения об электроэнергетических системах
- •Рис.1.1 Структурная схема энергетической системы
- •1.3. Общие сведения о схемах замещения
- •1.4. Система обозначений
- •1.5. Применение уравнений законов Кирхгофа
- •1.6. Уравнения узловых напряжений
- •1.7. Уравнения контурных токов
- •2. ПРИМЕНЕНИЕ АЛГЕБРЫ МАТРИЦ И ТЕОРИИ ГРАФОВ К РАСЧЕТУ РЕЖИМОВ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ И СЕТЕЙ
- •2.1. Общие положения
- •2.2. Некоторые сведения из алгебры матриц
- •2.3. Схема замещения сети как связанный направленный граф
- •2.4. Матрицы соединений графа электрической сети
- •2.5. Независимые параметры режима электрической цепи
- •3.1. Обобщенное уравнение состояния
- •3.2. Уравнение узловых напряжений
- •3.3. Уравнение контурных токов
- •3.4. Обобщенные параметры схем электрических систем
- •4.1. Линейные и нелинейные уравнения состояния
- •4.2. Особенности систем линейных уравнений и методы их решения
- •4.3. Решение уравнений состояния методом Гаусса
- •4.3.1. Метод Гаусса с обратным ходом
- •4.3.2. Метод Гаусса без обратного хода (метод Жордана)
- •4.3.3. Сравнительная вычислительная эффективность методов Гаусса с обратным ходом и без обратного хода
- •4.4. Применение обратных матриц для решения уравнений
- •4.4.1. Классический метод получения обратной матрицы
- •4.4.3. Обращение матрицы коэффициентов методом перестановки столбцов
- •4.4.4. Получение обратной матрицы методом факторизации
- •4.5. Итерационные методы решения систем линейных уравнений
- •4.5.1. Метод простой итерации
- •Таблица 4.4
- •4.5.2. Метод Зейделя
- •4.6. Методы решения нелинейных систем уравнений
- •4.6.2. Применение метода внешней итерации
- •4.6.3. Применение итерационных методов для решения нелинейных уравнений
- •4.6.4. Применение метода Ньютона для решения одного уравнения
- •5. МЕТОДЫ ОПТИМИЗАЦИИ РАСЧЕТОВ РЕЖИМОВ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ
- •5.1. Приведение комплексных уравнений к системе действительных уравнений
- •5.2. Учет слабой заполненности матриц коэффициентов уравнений состояния при расчетах установившихся режимов
- •5.4. Разделение на подсистемы
- •6. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ МАТРИЧНЫМИ МЕТОДАМИ
- •6.1. Составление схем замещения электрической сети
- •6.2. Примеры решения задач
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

96
(i +1)
Значение напряжения, вычисленное с ускорением, U k уск принимается в качестве исходного при расчете следующего (i + 2)- го шага.
В случае q = 1 |
(i +1) |
выражение (4.23) сводится к U k уск |
ный итерационный процесс соответствует случаю, когда ент q принимается равным единице.
= U (ki +1), т.е. неускорен-
ускоряющий коэффици-
Основное достоинство метода в том, что он легко программируется и требует малой памяти ЭВМ. Недостаток метода состоит в медленной сходимости. Метод Зейделя особенно медленно сходится, а в ряде случаев и расходится в расчетах установившихся режимов электрических систем с устройствами продольной компенсации, с трехобмоточными трансформаторами или автотрансформаторами с очень малым сопротивлением обмотки среднего напряжения и для электриче-
ских систем с дальними линиями электропередачи и сильной неоднородностью параметров. Метод Зейделя также плохо сходится либо расходится в расчетах режимов, близких к предельным, либо при определении режимов, неустойчивых по статической апериодической устойчивости.
4.6.4. Применение метода Ньютона для решения одного уравнения
Метод Ньютона весьма эффективен для решения нелинейных алгебраических и трансцендентных уравнений. Его основное достоинство состоит в том, что при сравнительно несложном алгоритме он обладает быстрой сходимостью. Метод Ньютона универсален и пригоден для решения обширного класса нелинейных уравнений.
Идея метода Ньютона состоит в последовательной замене на каждой итерации нелинейной системы уравнений некоторой линейной, решение которой дает значения неизвестных, более близкие к решению нелинейных систем, чем исходное приближение.
W x |
0 |
W х |
W х 1
х
2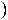 1
1 0
0
Рис.4.1. Пояснения к методу Ньютона
Алгоритм метода состоит в том, что если задаться некоторым нулевым приближением и вычислить функцию для этого приближения, затем рассчитать про-

97
изводную функции в этой точке, то, используя геометрический смысл производной (тангенс угла наклона касательной), можно определить новое значение
есть новое приближение аргумента. Затем находят значение функции в точке x(1),
значение производной функции в этой точке и новое приближение x(2) и т.д. Следует отметить, что контроль сходимости по величине разности значений переменных на соседних интервалах может привести к неверным результатам. Считают, что итерационный процесс сходится, если функция W (x) становится близкой к нулю, то есть W (x(i )) £ e .
Допустим, что имеется функция W (x) = 0 . Зададимся произвольным значе-
нием аргумента x(0) и определим значение функции W (x(0)). Определим производную функции:
|
|
dW (x(0)) |
= tga . |
|
(4.24) |
|||||||
|
|
|
dx |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
Согласно рис. 2.1 можно записать: |
|
|
||||||||||
|
dW (x(0)) |
|
|
|
W (x(0)) |
|
|
|||||
|
|
|
|
|
|
= |
|
(x(0 )- x(1 )). |
|
(4.25) |
||
|
|
|
dx |
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
W (x(0)) |
|
|
||
|
x |
(1 ) |
= x |
(0 ) |
- |
. ) |
(4.26) |
|||||
|
|
|
|
|
dW (x(0 ) |
|||||||
dx
Это выражение позволяет определить новое значение аргумента, которое является очередным приближением искомого корня, если итерационный процесс продолжается.
Данное выражение можно несколько преобразовать:
x(1) = x(0) + Dx(1), |
(4.27) |
где
Dx(1 ) = - W (x((0(0))) . ) dW x
dx
В общем случае для (i +1)- го шага итерации можно записать:
x(i +1) = x(i ) |
+ Dx(i +1); |
|
(4.28) |
|||
Dx |
(i +1 |
) |
W (x(i)) |
|
|
|
|
= - |
dW (x(i ) |
. |
) |
(4.29) |
|
dx
Итерационный процесс ведется до тех пор, пока значение функции W не
будет удовлетворять точности e :
W (x(i+1))£ e.

98
В отличие от ранее рассмотренных итерационных методов здесь для -кон троля не применяется разность, так как заранее известно, что в точке решения функция обращается в нуль. Поэтому e отражает допустимую величину отличия функции от нуля, то есть величину погрешности определения точного решения.
4.6.5. Применение метода Ньютона для решения систем уравнений любого порядка
Рассмотрим алгоритм применения метода Ньютона на примере решения системы нелинейных уравнений третьего порядка:
ìï a11x1 +a12 x2 + a13x3 = b1 ía21x1 +a22 x2 + a23x3 = b2
ïîa31x1 +a32 x2 + a33x3 = b3 ,
где b1 , b2 , b3 - функции нескольких переменных: b1 = f (x1 ,x2 ,x3 ) b2 = f (x1 ,x2 ,x3 ) b3 = f (x1 ,x2 ,x3 ).
Приведем функции к виду:
W1 (x1, x2 , x3 ) = 0 W2 (x1, x2 , x3 )= 0
W3 (x1, x2 , x3 ) = 0.
Если считать, что система уравнений матричная, то можно записать:
W(x)= 0 ,
где
éx1 ù
x= êêx2 úú .
êx ú ë 3 û
Будем считать, что заданы значения нулевых приближенийx1(0), x2(0), x3(0).
Используя описанный выше метод касательных, заменим каждую из нелинейных функций линейной, пользуясь при этом разложением в ряд Тейлора, то есть представим уравнения в следующем виде:
W1 (x1(0 ), x20( ,)x30 ()+) |
¶W |
(x(0), x(0) |
, x |
(0)) |
(x1(1) - x1(0 ))+ |
¶W |
(x(0) |
, x |
(0) |
, x(0)) |
(x2(1 ) - x2(0 ))+ |
||||
1 |
1 |
2 |
|
3 |
|
1 |
1 |
|
2 |
3 |
|
||||
|
|
¶x1 |
|
|
|
|
¶x2 |
|
|||||||
|
|
|
|
|
|
|
14243 |
|
|
|
14243 |
||||
|
|
|
|
|
|
|
|
Dx(1 ) |
|
|
|
|
|
|
Dx(1 ) |
|
¶W1 (x1(0 ), x20( ,)x30 ()()x3(1) - x3(0 ))= 0 |
1 |
|
|
|
|
|
|
2 |
||||||
+ |
|
|
|
|
|
|
|
(4.30) |
|||||||
|
¶x3 |
14243 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Dx |
(1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|

99
W2 (x1(0 ),x20( ,)x30 ()+) |
¶W |
(x(0) |
,x(0) |
,x(0)) |
(x1(1 ) - x1(0 ))+ |
|
¶W |
(x(0) |
,x |
(0) |
,x |
(0)) |
(x2(1 ) - x2(0 ))+ |
||||||||||||||||||
|
|
2 |
1 |
2 |
3 |
|
|
2 |
1 |
|
2 |
|
3 |
|
|||||||||||||||||
|
|
|
¶x1 |
|
|
|
|
¶x2 |
|
|
|
||||||||||||||||||||
|
|
(x |
(0 ) |
0( |
) 0 ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
¶W2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
,x |
2 |
,x |
3 |
) |
(x3(1 ) - x3(0 ))= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
¶x3 |
|
|
|
|
|
|
(x(0) |
, x(0) |
, x(0)) |
|
|
|
|
|
(x(0) |
, x(0) |
, x(0) ) |
|
|
|
|||||||
(0 ) |
|
0( |
) |
0 ( ) |
¶W |
(1 ) |
0 |
|
¶W |
(1 ) |
(0 ) |
|
|||||||||||||||||||
|
|
|
3 1 |
2 |
3 |
|
|
|
3 1 |
|
2 |
|
3 |
|
|
|
|||||||||||||||
W3 (x1 |
, x2 |
, x3 |
)+ |
|
|
|
|
|
|
|
|
(x1 |
- x1 |
)+ |
|
|
|
|
|
|
|
|
|
(x2 |
- x2 |
)+ |
|||||
|
|
|
¶x1 |
|
|
|
|
|
¶x2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ ¶W3 (x1(0 ), x20( ,)x30 ()()x3(1 ) - x3(0 ))= 0.
¶x3
Суть метода состоит в том, что нелинейная система уравнений заменяется линейной с использованием частных производных. Полученная система решается относительно приращений аргумента Dx1 , Dx2 , Dx3 .
В матричном виде: |
|
|
|
|
|
¶W(X0 )(X(1 ) - X(0 ))= 0 . |
|
|||||||||||||||
|
|
|
|
|
|
W(X(0 ))+ |
(4.31) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶X |
|
|
|
14243 |
|
|||
В этом выражении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DX |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
é ¶w |
|
¶w |
|
|
|
¶w ù |
|
|
||||||||||
|
|
|
|
ê |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
ú |
|
|
||
|
|
|
|
|
¶x |
|
¶x |
2 |
¶x |
|
|
|||||||||||
|
¶W(X) |
|
ê |
1 |
|
|
|
|
|
|
3 |
ú |
|
|
||||||||
|
|
ê |
|
¶w |
¶w |
|
|
¶w |
|
|
ú |
|
|
|||||||||
|
|
|
= |
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|||||
|
¶X |
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
||||||
|
|
ê ¶x |
|
2 |
|
|
|
|
|
¶x |
ú |
|
|
|||||||||
|
|
|
|
ê |
1 |
|
|
|
|
|
|
3 |
ú |
(4.32) |
|
|||||||
|
|
|
|
|
¶w |
|
¶w |
|
|
¶w |
|
|||||||||||
|
|
|
|
ê |
|
3 |
|
|
|
|
3 |
|
|
|
3 |
|
ú |
- матрица |
частных производн |
|||
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|||||||||
|
|
|
|
ê |
|
¶x |
|
2 |
|
|
|
|
|
¶x |
ú |
|
|
|||||
|
|
|
|
ë |
1 |
|
|
|
|
|
|
3 |
|
|
û функции Wi на каждом шаге итерации – |
|||||||
матрица Якоби.
éx1(1) - x1(0)ù
Матрица DX(1) = êêx(21 ) - x(20 )úú получила название матрицы поправок. (4.33)
êêëx(31 ) - x(30 )úúû
Если начальные приближения x1(0),x2(0),x3(0) заданы, то матричное выраже-
ние можно записать в виде: |
|
|
|
|
|
||
|
dW(X(0)) |
|
(1 ) |
|
(0 ) |
|
|
|
|
|
DX |
|
= -W(X |
). |
(4.34) |
|
|
|
|
||||
dX
Учитывая, что вектор X(0) - задан, получим, что коэффициенты матрицы Якоби оказываются числовыми значениями, и последнее выражение представляет
собой обыкновенную систему уравнений, которая разрешается относительно
DX (1).

100
Если матрица Якоби не вырождена (то есть ее определитель не равен нулю), то решение может быть получено, в том числе, и по методу Гаусса. После этого
можно найти первое приближение:
X (1) = X (0) + DX (1).
Таким образом, каждый шаг итерационного процесса представляет собой
решение линейной системы уравнений |
|
|
W(X(i ))+ |
¶W(X(i))(X(i+1 )- X(i ))= 0 |
(4.35) |
или |
¶X |
|
|
|
|
¶W(X(i))DX(i+1 )= -W(X(i )). |
(4.36) |
|
¶X |
|
|
Далее определяются следующие приближения неизвестных. Решение ве-
дется до тех пор, пока не выполнится условие:
W(X(i+1))£ e.
Метод Ньютона использует на каждом шаге решение линейной системы уравнений, получаемой с использованием частных производных в процессе -ли неаризации, что создает более целенаправленное движение к получению решения и сокращает количество итераций, необходимое для получения решения с заданной точностью.
4.6.6. Применение метода Ньютона для решения уравнений узловых напряжений
Пусть имеется сеть из трех узлов. Запишем для такой сети уравнения узловых напряжений, считая узел 3 балансным
*
Y 11U 1 + Y 12U 2 = S* 1 - Y 13U 3
U 1
*
Y 21U 1 + Y 22U 2 = S* 2 - Y 23U 3 .
U 2
Будем считать, что мощности имеют постоянную величину, и вследствие этого система является нелинейной. Придадим уравнениям вид функций, зависящих от напряжений U1 ,U 2 :

101
ì
ïï W1 (U 1,U 2 )= Y 11U 1 + Y 12U 2
ï
í
ï
ïW2 (U 1,U 2 )= Y 21U 1 + Y 22U 2
ï
î
или на i -ом шаге итераций:
*
- S* 1 + Y 13U 3
U 1
*
- S* 2 + Y 23U 3 ,
U 2
( (i )
W U
é
êY |
11 |
U |
(i ) |
+ Y |
12 |
U |
(i ) |
- |
|||
ê |
|
|
|
1 |
|
|
2 |
|
|||
|
|
|
|
|
|
||||||
= )ê |
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
(i ) |
|
|
|
(i ) |
|
|
ê |
|
|
U |
|
|
|
|
|
|||
êY |
21 |
|
1 |
+ Y 22 U |
2 |
- |
|||||
|
|||||||||||
êë
* |
|
|
|
|
|
|
|
|
|
ù |
|
|
S 1 |
|
|
|
|
|
|
|
|||
|
|
+ Y |
|
U |
|
ú |
|||||
|
* (i ) |
13 |
3 |
||||||||
|
|
|
|
|
|
ú |
|||||
U |
1 |
|
|
|
|
|
|
|
ú . |
||
|
* |
|
|
|
|
|
|
|
|||
|
S 2 |
|
|
|
|
|
|
|
ú |
||
|
|
+ Y |
|
|
U |
|
ú |
||||
|
* (i ) |
|
23 |
3 |
|||||||
|
|
|
|
|
ú |
||||||
|
|
|
|
|
|||||||
U |
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
2 |
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
||
Составим матрицу Якоби:
|
|
|
|
|
é |
|
|
|
* |
|
|
|
|
|
|
|
|
|
S1 |
|
|||
|
|
|
|
|
êY 11 + |
|
|
||||
|
|
|
|
|
æ * |
|
(i )ö2 |
||||
|
|
|
|
|
ê |
|
|
||||
|
|
|
|
|
ê |
|
çU |
|
|
÷ |
|
¶W ( |
U |
(i ) |
)ê |
|
ç |
|
|
1 |
÷ |
||
|
|
|
|||||||||
|
|
è |
|
|
|
ø |
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
= ê |
|
|
|
|
|
|
¶ |
U |
|
|
|
|
|
|
|
|
||
|
|
ê |
Y 21 |
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
ê |
|
|
|
|||
ê
ê
êë
|
|
|
ù |
|
Y 12 |
|
ú |
||
|
ú |
|||
|
|
|
ú |
|
|
|
|
ú |
|
|
* |
|
ú. |
|
Y 22 + |
S 2 |
|
ú |
|
|
ú |
|||
æ * (i )ö2 |
||||
|
ú |
|||
|
çU 2 |
÷ |
ú |
|
|
ç |
÷ |
ú |
|
|
è |
ø |
û |
|
Как видно из полученной матрицы Якоби, в этой матрице диагональные элементы зависят от искомых переменных. Этим она отличается от матрицы коэффициентов линейных уравнений. Анализ этой матрицы показывает, что структура ее, за исключением диагональных элементов, остается такой же, как и структура матрицы коэффициентов линейной системы уравнений узловых напряжений. Это позволяет использовать в методе Ньютона все способы оптимизации решения, применяемые для расчета режимов сложных энергосистем(учет разряженности, симметрия матрицы коэффициентов и др.). С другой стороны, для решения линеаризованных уравнений методом Ньютона не эффективно использование обратной матрицы, так как из-за зависимости диагональных элементов от значений переменных на каждом шаге итерации необходимо было бы обращать матрицу -ко эффициентов, что значительно уступает по эффективности методу Гаусса с обратным ходом.
Систему нелинейных уравнений можно записать в следующем виде:
¶W(U(i ) )DU(i +1 )= -W(U(i )). |
(4.37) |
¶U |
|
Тогда фактическое решение может быть записано следующим образом:
102
é |
|
(i+1) ù |
é |
|
(i ) |
+ DU |
(i+1) ù |
|||
U |
1 |
|
U |
1 |
1 |
|
||||
ê |
|
ú |
= ê |
|
|
|
ú. |
|||
|
|
+ DU |
||||||||
U |
(i+1 |
) |
U |
(i ) |
(i+1 |
) |
||||
ë |
|
2 |
û |
ë |
|
2 |
|
|
2 |
û |
|
|
|
|
|||||||
Итерационный процесс прекращается при выполнении условия:
W(U(i+1))£ e .
