Студентам_информатика / Лабораторные по информатике / Word_Вариант_10

Содержание

Введение.............................................................................................................

3

1 Интерполяция экспериментальных данных полиномами Лагража.....

4

1.1

Алгоритм метода интерполяции полиномами Лагранжа...................

4

1.2

Пример интерполяции полиномами Лагранжа ....................................

5

Заключение ........................................................................................................

7

Список литературы ...........................................................................................

8

1308. 5011ХХ.000ПЗ

Изм.

№ докум. Подп.

Лист

Дата

Разраб.

ФИО студента

Лит.

Лист

Листов

Пров.

Выполнение индивидуального задания в

Д

8

Рецен.

MS Word

УГАТУ ХХХ 1

Н контр

ФИО препод.

. .

Утв.

Стиль Заголовок 1

Введение

В инженерной практике часто возникают задачи построения

математической модели экспериментальных данных, данных наблюдений за

состоянием исследуемых процессов, наблюдений за изменением параметров

изучаемых объектов и т. д.

Стиль Основной_ПЗ

Суть построения математических моделей по экспериментальным данным

заключается в определении аналитической зависимости между переменными x и y

(функции y = f(x)) по значениям x и y в заданных узловых точках {yi , xi }. В

зависимости от того, как формируется данная функция, различают задачи

аппроксимации и интерполяции [2].

Перекрестная ссылка

Интерполя ция– способ нахождения

промежуточных значений

по

имеющемуся дискретному набору известных значений. Интерполяцией называют

такую разновидность аппроксимации, при которой кривая построенной функции

проходит точно через имеющиеся точки данных (рисунок 1).

Перекрестная

23

ссылка

21

19

17

15

13

y

11

9

7

5

3

1

Название

-1 0

0,2

0,4

0,6

0,8

1

x

Рисунок 1 – Геометрическое представление интерполяции

3

Изм.

№ докум.

Подп.

Дата

3

1 Интерполяция экспериментальных данных полиномами

Лагранжа

Стиль Заголовок 1

При интерполировании полиномиальной функцией требуется найти

коэффициенты ai интерполяционного полинома

Название

f ( x) = P ( x) = a

0

x n + a x n−1 + a

2

x n−2

+ ... + a

n

(1.1)

1

из условия строгого равенства

f ( x0 ) = y0 ,

f ( x1 ) = y1, ... ,

f ( xn ) = y n .

Функция f(x), согласно методу Лагранжа, подсчитывается по следующей

формуле:

n

( x − x1 )( x − x2 )...( x − xi−1 )( x − xi

+1 )...( x − xn )

,

f ( x) = ∑ yi

( x

− x )( x

− x

)...( x

− x

)( x

− x

)...( x

− x

i=1

i

i

2

i

i−1

i

i+1

i

n

)

1

или

n

n

x − x j

.

(1.2)

f ( x) = ∑ yi ∏

i=1 j =0 xi − x j

j ≠i

Интерполяционные формулы обычно используются при нахождении

неизвестных значений f(x) для промежуточных значений аргумента.

1.1 Алгоритм метода интерполяции полиномами Лагранжа

Рисунок 1.1 представляет блок-схему алгоритма вычисления значения

функции (интерполяционного многочлена) в заданной точке t [ x1, xn ] .

Перекрестная ссылка

Стиль Заголовок 2

4

Изм.

№ докум.

Подп.

Дата

4

Название

Рисунок 1.1 – Блок-схема алгоритма интерполяции полиномами Лагранжа

Стиль Заголовок 2

1.2 Пример интерполяции полиномами Лагранжа

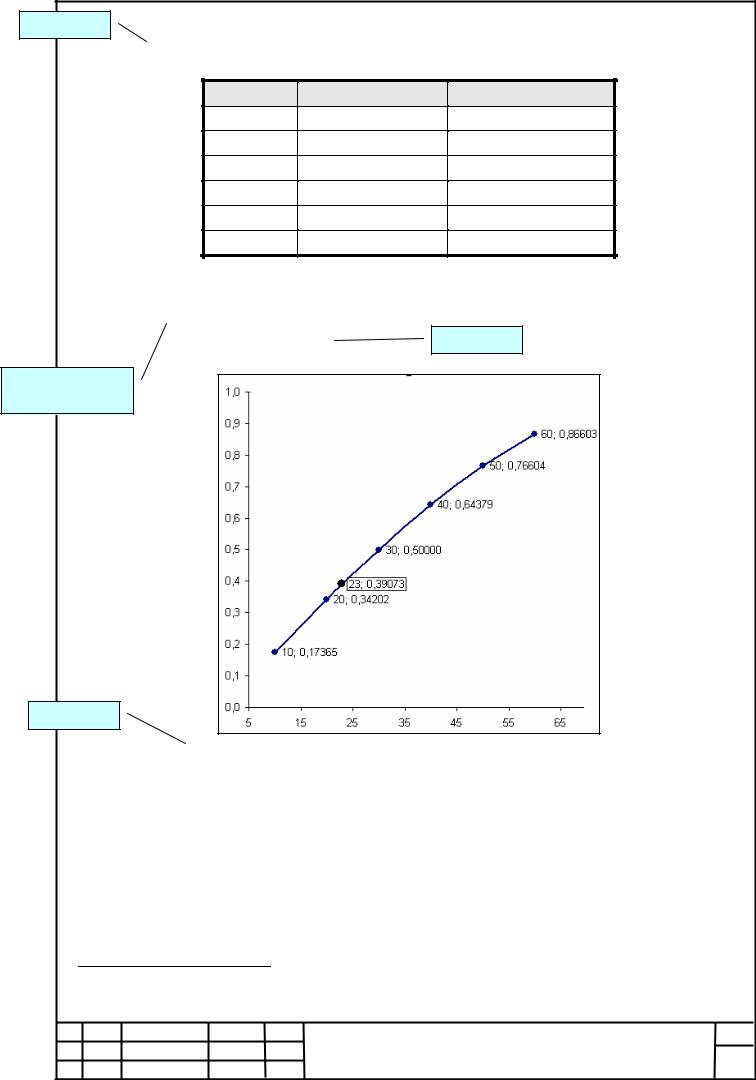
По

заданной

таблицей

значений

( x1 , y1 ), ( x2 , y 2 ), K, ( x6 , y6 )

найти

значение функции в точке x = 23 с помощью интерполяционного многочлена

Лагранжа (таблица 1.1).

Перекрестная ссылка

5

Изм.

№ докум.

Подп.

Дата

5

Название

Таблица 1.1

№ точки

Узловая точка x

Значение y

1

10

0,17365

2

20

0,34202

3

30

0,50000

4

40

0,64379

5

50

0,76604

6

60

0,86603

По формуле Лагранжа y = 0,39073 при x = 23.

Рисунок 1.2 представляет интерполяционную точку, полученную с

помощью полинома Лагранжа1.

Сноска

Перекрестная

ссылка

Название

Рисунок 1.2 –

Интерполяция многочленом Лагранжа

значений таблицы 1.1

1 На графике эта точка взята в рамку

6

Изм.

№ докум.

Подп.

Дата

6

Стиль Заголовок 1

Заключение

Предложенный способ построения интерполяционного полинома не

единственный. Кроме того, полином совсем не обязательно должен искаться

именно в форме Лагранжа. Поэтому выбор метода, типа интерполяционного

полинома и решение прочих подобных вопросов осуществляется, как правило, в

контексте конкретной решаемой задачи.

7

Изм.

№ докум.

Подп.

Дата

7