
Студентам_информатика / Лабораторные по информатике / Word_Вариант_12
.pdf
ФГБОУ ВПО Уфимский государственный авиационный технический университет
Кафедра Информатики
100 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
90
80
70
60
50
40
30
20
10
Выполнение индивидуального задания
в MS Word
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к лабораторной работе по информатике
1308.5011ХХ.000ПЗ
(обозначение документа)
|
|
|
|
|
|
|
|
|
Группа |
|
ХХХ |
|
Фамилия, И., О. |
Подпись |
Дата |
Оценка |
|
|
|
|
|
|
|
|
|
|
Студент |
|
|
ХХХХХХХХХ |
|
|
|
||
|
|
|
|
|
|
|
||
Консультант |
|
|
ХХХХХХХХХ |
|
|
|
||
|
|
|
|
|
|
|
||
Принял |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Уфа 2012 г.

|
Содержание |
|
Введение............................................................................................................. |
3 |
|
1 Численные методы решения систем линейных уравнений.................. |
4 |
|
1.1 |
Схема Халецкого ..................................................................................... |
4 |
1.2 |
Алгоритм схемы Халецкого ................................................................... |
5 |
1.3 |
Пример анализа электрической цепи .................................................... |
7 |
Заключение ........................................................................................................ |
8 |
|
Список литературы ........................................................................................... |
9 |
|
|
|
|
|
1308.5011ХХ.000ПЗ |
||||||
|
|
|
|
|||||||
Изм. |
|
№ докум. Подп. |
|
|||||||
Лист |
Дата |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Разраб. |
ФИО студента |
|
|
Лит. |
|
Лист |
Листов |
|||
|
|
|
|
|
|
|
|
|
|
|
Пров. |
|
|
Выполнение индивидуального задания в |
|
Д |
|
|
|
9 |
|
Рецен. |
|
|
MS Word |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
УГАТУ ХХХ 1 |
||
Н контр |
ФИО препод. |
|
|
|
|
|
||||
. . |
|
|
|
|
|
|
|
|
||
Утв. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Стиль Заголовок 1
Введение
Для того чтобы уметь решать конкретные задачи на компьютере,
недостаточно уметь правильно писать операторы на каком-либо языке программирования. Необходимо, прежде всего, знать алгоритмы и методы их решения. 

Инженеру часто приходится рассматривать задачи, которые сводятся к решению системы линейных алгебраических уравнений (СЛАУ). К таким задачам сводится большое число физических и технических проблем, возникающих,
например:
-при решении задач статической и динамической теории упругости,
упругопластичности, акустики и др.;
Маркированный список
-при анализе работы электрических цепей;
-при анализе процесса распространения тепла в сплошной среде (газе, жидкости или твёрдом теле) от более нагретых частей к менее нагретым;
-и т.д.
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
3 |
|
|
|
|


 Стиль Заголовок 1
Стиль Заголовок 1
1 Численные методы решения систем линейных уравнений
Способы решения систем линейных уравнений делятся на две группы:
1.прямые методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило
Крамера, метод Гаусса и др.), |
Нумерованный список |
|
|
2.итерационные методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации,
метод Зейделя и др.).
Вматричном виде система линейных уравнений записывается так
|
|
|
|
|
Ax = b , |
|
|
(1.1) |
||
|
a |
a |
K a |
|
x |
|
b |
|
|
|
|
11 |
12 |
1n |
1 |
|
1 |
|
Название |
|
|
|
a21 |
a22 |
K a2n |
x2 |
|
b2 |
|
|
||
где |
|
|
||||||||
A = K |
K |
K K |
, |
x = K |
, |
b = K |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an2 |
|
|
|
|
|
|
|
|
|
an1 |
K ann |
xn |
|
bn |
|
|
|
||
1.1 Схема Халецкого
Матрицу A можно представить в виде A = BC , где
b |
0 |
K 0 |
|
1 |
c |
|
|
|
11 |
|
|
|
|
12 |
|
b21 |
b22 |
K 0 |
0 1 |
K |
|||
B = |
K K K K |
, |
C = K K K |
||||
|
|
|
|
|
|
|
|
|
|
bn2 |
|
|
|
0 |
0 |
bn1 |
K bn4 |
0 |
|||||
c24
K .
1
Элементы bij и cij определяются по формулам
bi1 = ai1 , |
|
|
|
j −1 |
|
|
(1.2) |
|
|
||
bij = aij − ∑bik ckj |
для |
i ≥ j |
|
k =1 |
|
|
|
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
4 |
|
|
|
|

|
|
a |
|
|
|
|
|
|
|
|
c1 j = |
|
1 j |
, |
|
|
|
|
|
|
|
|
b11 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i −1 |
|
|
|
|
(1.3) |
|
1 |
|
|
|
|
|
||||
c = |
a |
− ∑b |
c |
|
для i < j |
|
||||
|
|
|
|
|||||||
ij |
b |
|
ij |
ik |
|
kj |
|
|
||
|
|
ii |
|
|
k =1 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
y1 = |
1,n+1 |
, |
|
|
|
|
|
||
|
|
|
|
|
|||||
|
|
b |
|
|
|
|
|
||
|
|
11 |
|
|
|
|
(1.4) |
||
y = 1 |
|
|
i −1 |
|
|
||||
|
(i > 1) |
|
|||||||
a |
+ − ∑b y |
|
|
||||||
i |
|
b |
i,n |
1 |
ik |
k |
|
|
|
|
|
ii |
|
|
k =1 |
|
|
|
|
Искомый вектор x может быть вычислен из цепи уравнений |
|
||||||||
|
|
|
By = b, |
Cx = y . |
|
|
|||
Так как матрицы B и C треугольные, то системы легко решаются. Из формул (1.2)
– (1.4) видно, что числа yi выгодно вычислять вместе с коэффициентами cij . Эта схема вычислений и называется схемой Халецкого.
1.2 Алгоритм схемы Халецкого
Рисунок 1.1 и рисунок 1.2 представляют блок-схему алгоритма метода Халецкого.
Перекрестная
ссылка
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
5 |
|
|
|
|

Рисунок 1.1 – Блок-схема формирования матриц B и С
Название
Название
Рисунок 1.2 – Блок-схема подсчета неизвестных xi (i = 1,…,n)
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
6 |
|
|
|
|
|
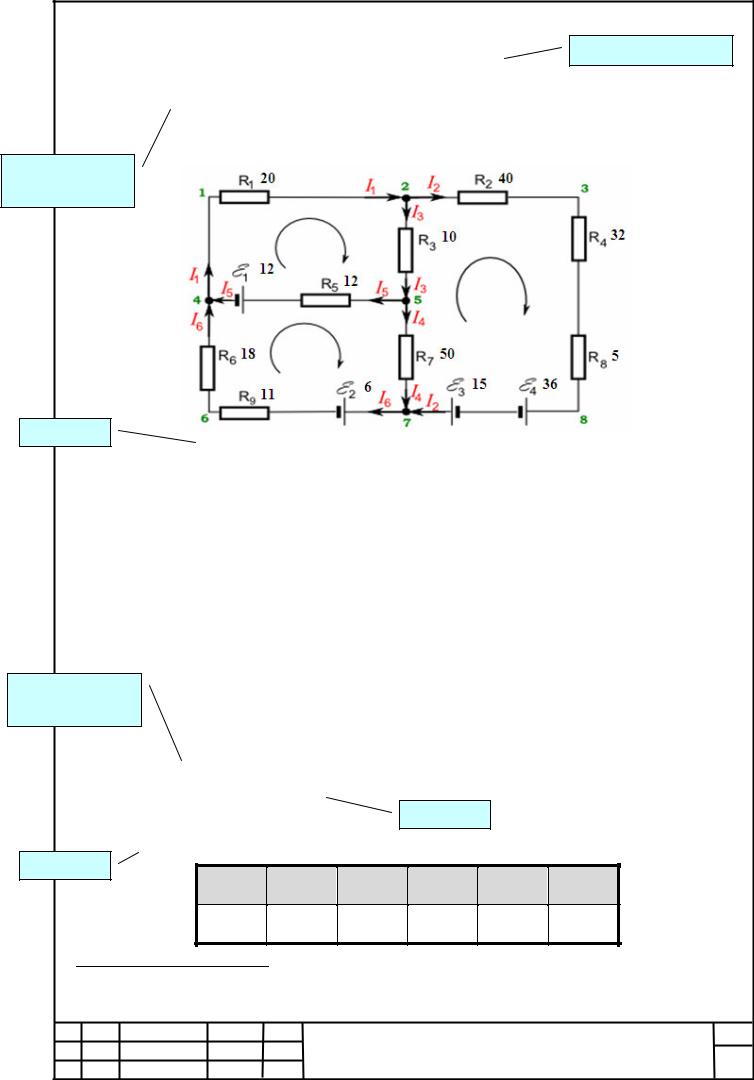
1.3 Пример анализа электрической цепи |
|
|
|
|
|
|
Стиль Заголовок 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
Рисунок 1.3 представляет многоконтурную электрическую схему с данными |
||||||||||||||||
сопротивлений, входящих в схему приборов. |
|
|
|
|
|
|
|
|
|
||||||||
Перекрестная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ссылка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Название |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.3 – Многоконтурная схема электрической цепи |
|||||||||||||||
|
Математическая модель этой задачи представляет собой систему линейных |
||||||||||||||||
уравнений, которая в матричной записи имеет вид |
|
|
|
|
|
|
|
|
|||||||||
|
|
20 0 10 |
0 |
12 |
0 |
I |
|
|
|
− 12 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
50 − 12 29 |
I 2 |
|
|
6 |
|
||||||
|
|
0 77 − 10 − 50 |
0 |
0 |
I |
3 |
|
|
|
− 21 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
1 − 1 − 1 |
0 |
0 |
0 |
I |
|
|
|
0 |
|
||||||
|
|
|
|
4 |
|
|
|||||||||||
Перекрестная |
|
|
− 1 0 |
0 |
0 |
1 |
1 |
|
|
5 |
|
|
|
0 |
|
|
|
|
|
|
|
I |
|
|
|
|
|
||||||||
ссылка |
|
|
0 |
1 |
− 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
− 1 0 |
I6 |
|
|
|
0 |
|
||||||||
|
Таблица 1.1 содержит значения токов, полученные после решения данной |
||||||||||||||||
системы линейных уравнений1. |
|
Сноска |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Таблица 1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Название |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
I 2 |
I 3 |
|
I 4 |
|
|
I 5 |
|
|
I 6 |
|||
|
|
-0,37 |
|
-0,22 |
-0,15 |
|
0,12 |
-0,26 |
|
|
-0,1 |
||||||
1 Решение системы линейных уравнений проводилось по схеме Халецкого |
|
|
|
|
|
|
|||||||||||
Изм. |
№ докум. |
Подп. |
Дата |
|
|
|
|
|
|
|
|
|
|
|
7 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||

|
|
|
|
Стиль Заголовок 1 |
|
Заключение |
|
|
|
|
Схема Халецкого относится к прямым методам решения систем линейных |
|||
уравнений [1]. Их эффективность зависит от порядка системы и структуры |
||||
матрицы. |
|
Перекрестная ссылка |
|
|
|
Прямые методы могут дать решение, если оно существует, с помощью |
|||
конечного числа арифметических и логических операций. Но при этом эти |
||||
методы накапливают ошибки округления. |
|
|||
Изм. |
№ докум. |
Подп. |
Дата |
8 |
|
||||

Стиль Заголовок 1
Список литературы
1.Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука, 1972. 366 с.
2.Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах MathCad 12, MatLab 7, Maple 9. М.: НТ Пресс, 2006. 496 с.
Нумерованный список
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
9 |
|
|
|
|
