алгем / 9-10_Affinnye_koordinaty

§ 9. Системы координат

1⁰. Аффинные системы координат на прямой, плоскости и в пространстве.

В предыдущем параграфе рассматривалось пространство геометрических векторов, представляющих собой семейства эквивалентных друг другу направленных отрезков. При этом в пространстве вводился базис, состоящий из трех некомпланарных векторов.

В этом параграфе в пространстве наряду с векторами будем рассматривать точки, и вместо базиса вводятся так называемые системы координат.

Пусть на прямой (на плоскости или в пространстве) заданы точка О и базис

Определение 1. Афиновой (декартовой) системой координат называется совокупность точки (начала координат) и базисных векторов, заданных в определенном порядке. Совокупность точки и базисных векторов иногда называют репером.

Декартова система координат, базис которой ортонормированный, называется декартовой прямоугольной системой координат.

Базисные вектора определяют координаты оси, проходящей через точку О и эти базисные вектора являются единичными (масштабными) векторами этих осей.

Замечание. а) Начало координат т. О делит ось координат на 2 полуоси: отрицательную и положительную.

б) Ось координат делит плоскость на координатные полуплоскости, а пара осей ­­- на координатные квадранты (четверти).

в) Плоскости, проходящие через пары осей называются координатными плоскостями.

г) Координатная плоскость делит пространство на 2 координатные полупространства, а тройка координатных плоскостей делит пространство на 8 координатных октант.

Если вести в рассмотрение точку M, то можно определить вектор , причем

(1)

Определение 2. Числа из формулы (1) называются аффинными координатами т. М в рассматриваемой системе координат.

Если рассматриваются две точки и , то координаты вектора находятся по следующему правилу:

Таким образом, чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.

Теперь рассмотрим, как преобразуются координаты точек при переходе от одной системы координат к другой. Пусть вначале центр системы координат переносится в точку , а базис не меняется. Если - радиус-вектор т.М в первоначальной системе координат, а - радиус-вектор преобразованной, то . Если , то из последней формулы имеем

Если теперь начало координат останется на месте, а базисные вектора преобразуются с помощью суммы, то координаты векторов в старом и новом базисах связаны формулами:

.

Объединяя оба преобразования получаем:

- формула преобразования координат точки при переходе от одного репера к другому.

2⁰. Задача деления отрезка в данном отношении.

Пусть в трехмерном пространстве с заданным репером рассмариваются две точки , .

Определение 3. Говорят, что точка делит отрезок в отношении , если .

Видно, что , если и , если ; .

Пусть точка M задана своими координатами, т.е.  , 

 (3)

Частный случай: деление отрезка пополам. Тогда =1 и координаты точки (середина отрезка) равны полусумме координат его концов.

Если и - радиус-вектора точек и , то формулы (3) могут быть переписаны в векторном виде: .

3⁰. Другие системы координат.

а) Полярная система координат.

Полярная система координат вводится на плоскости и задается точкой , которая называется полюсом, и координатной осью, проходящей через точку , которая называется полярной осью.

М

Положение произвольной точки М на плоскости в полярной системе координат определяется расстоянием от т. до т. М и углом , на который надо повернуть полярную ось против часовой стрелки до совмещения с осью ОМ.

Пара называется полярными координатами т.М, - полярный радиус, - полярный угол, .

С полярной системой координат естественным образом связывается прямоугольная декартова система координат: ось совпадает с полярной осью, ось проходит через полюс перпендикулярно (при повороте оси против часовой стрелки на угол ). Тогда полярная и декартова координаты т.М связаны формулами:

.

б) Цилиндрические координаты в пространстве.

Выберем в пространстве плоскость и введем на этой плоскости полярную систему координат. Через полюс О проведем ось перпендикулярно . Наряду с этим введем на плоскости прямоугольную декартову систему координат, соответствующую полярной.

Вместе с осью она будет образовывать декартову систему координат в пространстве.

Выберем произвольную точку М и рассмотрим проекции и точки М на ось и на плоскость .

Тогда точка имеет координату , а точка - полярные координаты .

Числа называются цилиндрическими координатами т. М в пространстве.

Таким образом, для того, чтобы ввести в пространстве цилиндрическую систему координат необходимо на некоторой фиксированной плоскости задать полярную систему координат и ось, перпендикулярную этой плоскости.

z

M

0

Если с циклической системой координат естественным образом связана декартова система координат, то координаты т.М в полярной системе координат и декартовой системе координат связаны формулами:

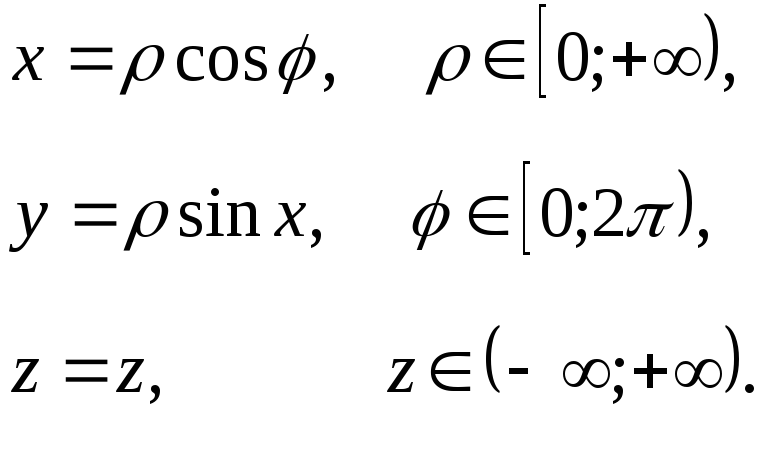
в) Сферическая система координат в пространстве.

Рассмотрим в пространстве декартову систему координат и соответствующую ей полярную систему координат в плоскости .

Пусть т.М – произвольная точка пространства, - проекция M на , имеющая полярные координаты и пусть - угол между и , - длина вектора . Тогда тройка определяет сферические координаты точки в пространстве. При этом используется следующая терминология: - радиус, - долгота, - широта. При этом

Если - координаты т.М в декартовой системе координат, то они связаны со сферическими координатами формулами:

Замечание. Иногда угол вводится как угол между и . Тогда формулы связи сферической с декартовой системой координат изменяются и выглядят следующим образом:

§10. Алгебраические линии и поверхности

Пусть на плоскости задана некоторая аффинная система координат. Тогда любая точка плоскости задается парой действительных чисел.

Определение 1. Множество точек плоскости, координаты которых в некоторой системе координат удовлетворяют уравнению

(1)

называется линией. Если уравнение (1) разрешимо относительно y, то оно переписывается

. (1’)

Иногда для описания линии используют векторную форму записи:

. (2)

Здесь параметр , - радиус-вектор точек на линии, при изменении t концы описывают некоторую линию.

Если на плоскости рассматривается декартова система координат, то каждый радиус-вектор может быть представлен . Тогда уравнение (2) в координатах принимает вид

(3)

- параметрическое уравнение линии.

Например, - уравнение окружности, а

- уравнение спирали (см. рис.).

Линию на плоскости иначе можно задать в полярной системе координат уравнением следующего вида:

,

где - длина , - полярный угол.

Например, - полярное уравнение линии.

Если перечисленные уравнения рассматривать парами, т.е.

или или или

Тогда каждая система определяет множество точек, являющихся пересечением двух линий.

Аналогично, множество решений уравнения

, (5)

можно рассматривать как поверхность в трехмерном пространстве, где - координаты точки в заданной системе координат. Если (5) разрешимо относительно одной из переменных, то оно может быть, например, переписано в виде

. (5’)

Замечание. Если уравнение поверхности (5) не содержит одной из переменных, то соответствующая поверхность называется цилиндрической.

Прямые линии, из которых она состоит, называются её образующими, а линию, лежащую на поверхности и пересекающую все образующие, называют направляющей.

Пример. Образующие и направляющая для поверхности (параболический цилиндр) приведены на рисунке.

Если рассматривать систему

, (6)

состоящую из двух уравнений поверхностей, то система (6) в общем случае описывает кривую пересечения этих поверхностей.

Пример. Множество всех решений системы

представляет собой окружность радиуса , расположенную на высоте 1/2 от плоскости Oxy.

Любую кривую в пространстве можно также описать в виде

(7)

- векторное параметрическое уравнение линии.

Если , то уравнение (7) в координатах принимает вид

(8)

- координатное параметрическое уравнение линии в пространстве.

Определение 2. Алгебраической поверхностью называется множество точек, которые в какой-либо аффинной системе координат удовлетворяют уравнению:

(9)

где . Величина наибольшей из сумм называется порядком алгебраической поверхности.

Аналогичное определение вводится для алгебраической линии на плоскости.

Теорема 1. Алгебраическая поверхность порядка p в любой аффинной системе координат может быть задана уравнением вида (9) порядка p.

Доказательство. Пусть в некоторой аффинной системе координат поверхность задана уравнением (9). Тогда при переходе в другую аффинную систему координат переменные преобразуются по формулам:

(10)

где - матрица перехода к другому базису, а вектор - координаты преобразованного начала координат. Очевидно, что после подстановки (10) в (9) порядок уравнений не повышается.

Если бы после подстановки (10) в (9) порядок полученного уравнения повысился, то в силу обратимости (10) порядок поверхности мог бы возрасти, а это невозможно. Таким образом, при переходе к другой системе координат порядок поверхности не изменяется, ч.т.д.∎