9. Дискретное преобразование Фурье.

Аналоговый сигнал: ;

t_k=k∙Δ (Δ – шаг дискретизации,k=0, ±1, ±2…).

Дискретизированный сигнал: .

Устройство выборки значений дискр. аналогового сигнала.

t_пр – время, необходимое АЦП для преобразования мгновенного значенияU_c в цифровые данные.

Спектральную плотность дискретизированного сигнала, состоящая из N отсчетов:

ω=n∙Δω.

- дискретное преобразование Фурье (ДПФ)

ω→n∙Δω.

kT→k

(n=0, ±1, ±2…± N/2) – алгоритм вычисления спектральных коэффициентов по временным отсчетамS(k).

{S[n]}; {S[k]}.

ОДПФ. Зная спектр. значения коэффиц-в можно определить выборки сигнала.

(k =0, 1, 2… N-1).

11.Теорема Котельникова

Непрерывный сигнал, спектр которого не содержит частот большеf_m, может быть однозначно представлен мгновенными значениями (выборками), разделенными одинаковыми интервалами времени, длина которых не должна превышатьТ<1/2∙f_m.

Дискретный сигнал:

Ω - частота поступления импульсов.

Спектр дискретного сигнала есть множественное повторение спектра аналоговых сигналов, следующих с частотойF=1/T.

Спектр цифрового сигнала:

S_T(ω)= S_T(Δω∙n)

Δω∙N=ω

ω= Δω∙n

- прямое преобразование Фурье.Позволяет по заданным временным отсчетамS[k] вычислять спектральные коэффициентыS[п].

Обратное преобразование Фурье: (n=0, ±1, ±2…± N-1).

10.Свойства дпф и одпф:

1. Линейность:

S1[k]	S2[k]
S1[п]	S2[п]

ДПФ

2. Нулевой коэффициент S [0] есть постоянная составляющая и является средним значением всех отсчетов.

3. Если S [k] действительные отсчеты иN – четное, то в данном случае имеет место симметричность сигнала:

4. Свертка дискретных сигналов:

S [k]	g[k]
S [п]	G[п]

(k =0, ±1, ±2… ±N-1).

ДПФ сигналов, отображающих циклическую свертку отсчетов, равно произведению спектральных плотностей соответствующих сигналов.

Быстрое преобразование Фурье (БПФ).Суть его заключается в нахождении в ДПФ и ОДПФ массивов с меньшим числом членов. ВMathCAD БПФ находится функциейfft(v).

12.Амплитудная модуляция

Модуляция – процесс управления одним или несколькими параметрами колебаний высшей частоты в соответствии с законом передаваемого сообщения.

При модуляции происходит процесс наложения передаваемого сообщения на другое колебание – несущее, f_нк>f_nc.

демодуляция– выделение принятого сообщения из модулированного колебания.

Модуляция дает возможность организации многоканальной связи по одной линии передачи. Выбор несущей частоты позволит повлиять на дальность передачи информационного сообщения. Передаваемый сигнал называют модулирующим. Несущее количество называютмодулируемым.

При амплитудной модуляции, в соответствии с законом передаваемого сообщения, меняется амплитуда модулируемого сигнала. При этом частота и фаза постоянны.

Однотональная модуляция возможна, если модулирующий сигнал представлен периодической функцией: S(t)=U_mcosΩt

Ω - частота распространения.

U_н(t)=U₀ cosω₀t; ω₀– частота распространения несущего колебания.

Рассмотрим случай Ω>>ω₀:

U (t)=U₀ (1+т∙cosΩt)cosω₀t

m – модуль (индекс) модуляции

U_огиб=U₀ (1+т∙S(t))

U(t)=U₀ cosω₀t+½∙m∙U₀∙cos(ω₀-Ω)t+½∙m∙U₀∙cos(ω₀+Ω)t

Диапазон спектра равен 2Ω

Ширина спектра амплитудно–модулированного сигнала равна удвоенному значению наивысшей частоты в спектре модулированного сигнала.

Пример:

0,5-1,5 МГц. В этом диапазоне необходимо организовать радиовещательные каналы со звуковым диапазоном до12 кГц. Какое количеств каналов можно организовать.

Решение:

Однополосная модуляция (SSB).

Балансная амплитудная модуляция (DSBSC):

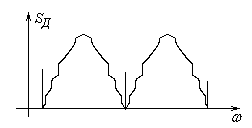
Данный вид модуляции широко используется для создания высокочастотных радиотелефонных каналов. Особенность приема SSB – сигнала заключается в наличии умножающего детектора, чтобы опять получить исчезнувшую несущую частоту.

Схемы генерации амплитудно-модулированных сигналов.

Простейшая схема генерации амлитуно-модулированных сигналов выглядит следующим образом:

Амплитудой сигнала управляют напряжением высокочастотного усилителя. Закон управления должен быть линейным.

При отсутствии модулированного сигнала транзистор VT1 (высокочастотный) смещен в активную область и работает в качестве усилителя ВЧ несущего колебания. ДроссельDR1 препятствует закорачиванию высокочастотной энергии на источник питания. КонденсаторС₁служит развязкой межу генератором модуляционного сигнала и источником питания. КонденсаторС₂согласует выходное сопротивление каскада и антенныА. Под действием модулирующего сигнала напряжения на коллекторе транзистора изменяется в соответствии с законом модулирующего сигнала, происходит положение на несущее колебание.