6.Спектральное разложение сигналов по тригонометрическим базисам.

Совокупность коэффициентов ряда Фурье в базисе тригонометрических функций – частотный спектр периодического сигнала.

Для разложения в ряд Фурье тригонометрическая базисная функция, описывающая измерительный сигнал (ИС), должна быть: периодической, интегрируемой, а так же не обращаться в бесконечность при разрывах.

Используется следующий набор функций:

1, cosωt, sinωt, cos2ωt, sin2ωt.

;

;

.

Если S(t)чётное, то, еслиS(t)нечётное, то.

Каждую гармонику можно охарактеризовать амплитудой и фазой. Тогда форма измерительного сигнала в тригонометрическом базисе выглядит следующим образом:

,

,

;

Комплексная форма записи.

Ряд Фурье может быть представлен в комплексной форме, если базисные функции записать в виде экспонент с мнимыми показателями.

.

7.Интегральное преобразование Фурье.

Гармонический анализ периодических сигналов можно распространить и на непериодические сигналы.

0<t<T (ω=2πT)

.

Для перехода к предельному непериодическому сигналу необходим устремить Т→∞.

При Т→∞:

1. ω→dω

2. n∙ω→ω

3. сумма→dω

.

Основные свойства преобразования Фурье:

1. линейность: S₁(t)→ S₁(ω)… S_n(t)→ S_n(ω)

2. преобразование Фурье сигнала, смещенного во времени

S (t)↔ S (ω); S(t-t₀); S’(ω)-?

│x=t-t₀│

3. преобразование Фурье производной сигнала

S (t)↔ S (ω);

F(ω)-?

F(ω)=jωS(ω).

Для n-ой производной F(ω)=(jω)²S(ω).

4. преобразование Фурье произведения сигналов

U(t)↔ U (ω); V(t)↔ V(ω);

Сверка спектральных плотностей:

.

Произведению сигналов соответствуют спектральная плотность, пропорциональная свертке этих сигналов.

8.Спектральная плотностьизмерительного сигнала есть характеристика частоты. Является комплексно-значимой характеристикой, несущей информацию и об амплитуде и о фазе измерительного сигнала.

Спектральная плотность обладает всеми свойствами спектральных коэффициентов с отличием в Ом, что в спектре непериодического сигнала присутствуют все частоты. Формулу для S(ω)называютпрямым преобразованием Фурье.

Формула обратного преобразования Фурьевыглядит следующим образом:

.

Условие наличия спектральной плотности у сигналов:

1. δ(t) (при t=0, δ(t)=∞, при t≠0, δ(t)=0) ; S(t)=A∙δ(t),

;t=0; S(ω)=A∙e⁰=A

2. прямоугольный импульс.

τ_и­ - длительность импульса.

;;S(ξ=0)=Uτ_u.

3. экспоненциальный видеоимпульс

S(t)=U∙e^-αtδ(t).

.

; ; ; ; .

Для описания интегрированной плотности неинтегрируемых сигналов вводится понятие обобщенной спектральной плотности. Для этого рассматривают дополнительную функцию, которая является абсолютно интегрируемой и имеет спектральную плотность S(ω) и связана с исследуемым сигналомформулой Релея:

;

1. постоянный сигнал. U(t)=A, V(t), V(ω)

;.

Используя фильтрующие свойства δ – функции, получимU(ω)=2π∙A∙δ(ω).

2. 

3.

4.

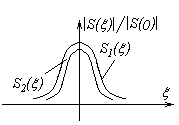
Вывод: чем больше длительность импульса, тем меньше ширина его спектра. Это важно для определения частотного диапазона аппаратуры, обрабатывающей сигнал (ей надо обеспечить широкую полосу пропускания).