28.Структурная реализация дискретных(цифровых) фильтров.

, где

a_i, b_l – коэффициенты цифрового фильтра.

Если все a_iиз первого слагаемого равны нулю, то получаемнерекурсивный фильтр(трансверсальный).

Передаточная функция будет выглядеть следующим образом:

- проводим взвешенное суммирование отсчетов только входного сигнала и не учитываем предшествующие отчеты выходного сигнала, если хотя бы одинa_i≠0, то.

В этом алгоритме фильтрации форма выходных отчетов используется предыдущими значениями как входного, так и выходного сигналов.

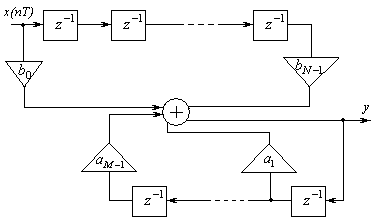
Структура нерекурсивного фильтра.

.

Данная схема обеспечивает установить при любых b_l.

x(nT)={1,0,0…}

{h_l}={b₀, b₁,…b_N-1}

Реакция данного фильтра на единичное воздействие будет определяется конечным числом коэффициентов b_l.

H(z)→k(jω).

Подбирая b_l, зададим нужные АЧХ и ФЧХ.

29.Структура рекурсивного фильтра.

а₀=1.

Основной недостаток: потребность большого число ячеек памяти. Более совершенной является каноническая форма рекурсивного цифрового фильтра. Минимальное число ячеек определяется как наибольшее число порядков числителя или знаменателя.

Напр. для рекурсивного ф. 2 порядка:.

Пусть заданы начальные условия:

{y_i-1, y_i-2,…}, то в отсутствии входного сигналах_k фильтр будет образовывать бесконечную последовательность {y_i, y_i+1,…}, имитирующую свободные колебания цифрового фильтра.

Рекурсивный цифровой фильтр называется устойчивым, если последовательность {y_п}≤М, М – некоторое положительное число, прип→∞.

Если │α_i│≤1, то любой свободный процесс в цифровом фильтре будет описываться членами убывающей геометрической прогрессии, и фильтр будет устойчивым.

При воздействии единичного импульса на рекурсивный фильтр на выходе будет реакция, представляющая собой неограниченную протяженную последовательность.

30.Методы синтеза линейных цифровых фильтров.

Синтез цифровых фильтров.

Три основные операции:

1. сложение двух отсчетов:

2. умножение:

3. задержка сигнала на один шаг дискретизации:

1. Метод подобных импульсных характеристик

Синтезированный фильтр должен обладать импульсной характеристикой, которая является результатом дискретизации импульсной характеристики соответствующего аналогового фильтра.

Для нерекурсивного фильтра:

• {h_k}={h(0), h(Δ), h(2Δ)}; (h(t)→h_k)

• z – преобразование H(z)

;

- для рекурсивного фильтра.

2. Дискретизация дифференцированного уравнения аналоговой цепи.

; .

Получим рекурсивный фильтр, который буде являться аналогом колебательного звена второго порядка.

3. Метод подобных частотных характеристик. Частотный коэффициент цифрового фильтра является периодической функцией частоты с периодом, определяемым шагом дискретизации. Поэтому говоря о подобном, можно лишь требовать сохранения общего вида АЧХ на интервале: .

Пусть задана передаточная функция К(р), требуется найти такую дробно – рациональную функциюH(z), которая отражала бы взаимосвязь параметровp иz.

.

Для фильтров второго порядка:

- для синтеза фильтра низких частот.

K(p)→H(z)→│K(jω)│→АЧХ.

Входная отсчетная последовательность, обусловленная шумом квантования:

.

Дисперсия выходного сигнала по шуму квантования:

.

Выходной шум квантования тем больше, чем медленнее уменьшаются отсчеты импульсной характеристики фильтра.