26.Цифровая обработка сигналов

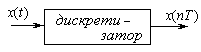
Связь спектра дискретной последовательности x(nT)обозначается как:

, где

- частота дискретизации;x_а – спектр аналогового сигнала.

Из формулы видно, что спектр последовательности x(nT)равен с точностью до множителя1/Тсумме спектров соответствующего аналогового сигналаx_а(T), смещенного по оси частот на все возможные значенияω, кратные частоте дискретизации.

далее Z-преобразование.

Алгоритм линейной цифровой фильтрации.

Теория линейных фильтрация (ЛФ) не теория линейных стационарных систем.

Для ЛCC:

(**)

Линейным цифровым фильтром называется дискретная система (или физическое устройство, или программное управление), которая преобразует последовательность входных числовых отсчетов {x_k} в последовательность выходных числовых отсчетов {у_k}.

Основным свойством линейной цифровой фильтрации является преобразование суммы любого числа входных сигналов «*» на производные коэффициенты в сумму его откликов на отдельные слагаемые.

Пусть {x_k¹}→{y_k¹}…{x_k⁽ⁿ⁾}→{y_k^(m)}

α₁∙{x_k}+… α_k∙{x_k¹} {α₁∙y_k¹+… α_k∙y_n⁽ⁿ⁾}.

Введем понятие импульсной характеристикицифрового фильтраh_k(h_k – есть дискретный сигнал являющийся реакцией цифрового фильтра на единичный импульс).

{x_k} {1,0,0,0}

{h_k} {h₀,h₁,h₂,h₃}

Линейный фильтр может быть стационарным, если при смещении единичного импульса на любое число интервалов дискретизации его импульсная характеристика смещается таким же образом, не изменяясь по форме.

{х_k}={х₀,х₁,х₂,… } ; .

Выходная последовательность есть дискретная свертка входного сигнала и импульсной характеристики фильтра. При каждом отсчете цифровой фильтр проводит процесс взвешенного суммирования всех предыдущих значений входного сигнала.

Роль последовательных весовых коэффициентов выполняют отсчеты импульсной характеристики, что предполагает обладания фильтром некой памяти по отношению к прошлым входным воздействиям.

Для физической реализуемости цифровой фильтрации импульсная характеристика {h_k}=0в отсчетных точках, предшествующих моменту подачи входного сигнала, следовательноk≥0.

Частотный коэффициент передачи.

Пусть на вход цифрового фильтра пришел сигнал:

;приk=0;±1;±2…

После преобразования получим:

примем m-k=n, тогда

k(jω) – частотный коэффициент передачи цифрового фильтра он зависит от шага дискретизации, от частоты и от совокупности коэффициентов импульсных характеристик.

1. k(jω)есть периодическая функция сω=ω_Д=2π/Δ.

2. k(jω) есть преобразование Фурье импульсной характеристики цифрового фильтра.

Передаточная функция цифрового фильтра определяется через z – преобразование входного и выходного сигнала при нулевых начальных условиях.

.

Принцип цифровой обработки сигналов.

Базовая структурная схема цифровой обработки выглядит следующим образом:

Входной сигнал х(t) поступает на аналоговый цифровой преобразователь, преобразующий его в сигнал в виде двоичного числа с фиксированным количеством разрядов.

В зависимости от устройства аналогового цифрового преобразователя, это число может быть представлено либо в последовательном, либо в параллельном коде, далее полученная выборка поступает в процессор, где хранится алгоритм обработки сигналов.

В блоке памяти содержится предшествующее значение входного и выходного сигналов.

В ЦАП в сочетании с ФНЧ задействует в тех случаях, когда выходной сигнал требуется получить в аналоговой форме.

27. z – преобразованиепоследовательностейx(nT)определяется рядом:

(*)

z – комплексная переменная, которая может быть представлена в виде реальной или мнимой части:.

Если x(nT), то считаемx(k). Если отсчетыx(k) есть значения непрерывной функции x(Т)в точкахТ=k∙Δ (Δ – шаг дискретизации), то любому сигналу x(Т)можно сопоставить его z – преобразование при выбранном шаге дискретизации.

Для сходимости ряда (*) достаточно выполнение этого условия:.

Область сходимости определяется окружностью, минимальным радиусом Rвz – плоскости. Вне радиуса ряд сходится.

Обратное z – преобразование.

Позволяет оценить минимальный отсчет, зная изображение сигнала.

р – комплексная частота: р=α+jω

Преобразование Лапласа для дискретного сигнала:

e^-p∙Δ=z .

Все свойства выполняются и для дискретного преобразования и для преобразования Лапласа.

Свойства z – преобразования:

1. свойство линейности

x1(nT)	→ х1(z)
х2(nT)	→ х2(z)

Если соответствует, то:

2. z – преобразование смещенного сигнала

x(nT) соответствует x(z), причемx(nT)=0 прип<0

y(nT)=x(nT-mT) соответствовать будет

, гдеz^-m – оператор сдвига нат – интервалов вz – плоскости.

3. z –изображение свертки сигналов

x1(nT)	→ х1(z)
х2(nT)	→ х2(z)

.