ТОИИТ1 / кол 2

Содержание

1 Введение 2

2 Теоретическая часть 4

2.1 Классификация фильтров 4

2.2 Аппроксимация активных фильтров 5

3 Расчетная часть 7

3.1 Расчет фильтра Баттерворта на основе МОС 7

3.2 Расчет фильтра Чебышева на основе МОС 9

4 Заключение 11

Список литературы 12

1 Введение

Электрический фильтр представляет собой частотно-избирательное устройство, пропускающее сигналы определённых частот и задерживающее или ослабляющее сигналы других частот.

Диапазоны частот, в которых сигналы проходят, называются полосами пропускания и в них значение амплитудно-частотной характеристики относительно велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, образуют полосы задержки и в них значение амплитудно-частотной характеристики относительно мало, а в идеальном случае равно нулю.

Фильтрация – наиболее распространенный способ обработки сигналов, имеющий своей целью подавление нежелательных составляющих (шумов, помех) и сохранение (или усиление) информативных составляющих.

Электрические фильтры можно подразделить на два больших класса: активные и пассивные фильтры.

Пассивные фильтры представляют собой устройства, которые создаются на основе резисторов, конденсаторов и катушек индуктивности, т.е. из пассивных схемных элементов. Эти фильтры пригодны для работы в определенных диапазонах частот, но не подходят для низких частот, например ниже 0,5 МГц. Это происходит вследствие того, что на низких частотах параметры требуемых катушек индуктивности становятся неудовлетворительными из-за их больших размеров и значительного отклонения рабочих характеристик от идеальных. Кроме того, в отличие от резисторов и конденсаторов, катушки индуктивности плохо приспособлены для интегрального исполнения.

Таким образом, для применения фильтров в диапазоне низких частот из схем желательно исключить катушки индуктивности. Это достигается разработкой активных фильтров на основе резисторов, конденсаторов и одного или нескольких активных приборов, таких как транзисторы, зависимые источники и т.д. Наиболее часто в качестве активного прибора применяются операционные усилители.

2 Теоретическая часть

2.1 Классификация фильтров

Основной классификацией фильтров является классификация по виду амплитудно-частотной характеристики, согласно которой фильтры подразделяются на:

– фильтры низких частот (рисунок 1, а);

– фильтры высоких частот (рисунок 1, б);

– полосно-пропускающие фильтры (рисунок 1, в);

– полосно-заграждающие или режекторные фильтры (рисунок 1, г)

Рисунок 1 – АЧХ идеальных фильтров

Фильтры низких частот имеют полосу пропускания и полосу задержки .

Фильтры высоких частот имеют полосу задержки и полосу пропускания .

Полосно-пропускающие фильтры имеют полосу пропускания и полосы задержки и .

Полосно-заграждающие фильтры имеют полосу задержки и полосы пропускания и .

Кроме частотно-избирательных фильтров можно получить фильтры, для которых важным параметром является фазо-частотная характеристика: фазосдвигающий и времязамедляющий.

Фазосдвигающий фильтр – фильтр, амплитудно-частотная характеристика которого неизменна, а фазо-частотная характеристика изменятся в зависимости от частоты.

Во времязамедляющем фильтре основной интерес представляет характеристика времени замедления

.

Он рассчитывается таким образом, что почти постоянна для выбранного диапазона частот.

2.2 Аппроксимация активных фильтров

Идеальные прямоугольные АЧХ фильтров физически не реализуемы. Можно лишь стремиться к наилучшему приближению (аппроксимации), совместимому с требованиями, предъявляемыми к фильтру.

При аппроксимации по Баттерворту АЧХ фильтра определяется выражением:

,

где для ФНЧ и для ФВЧ – относительная частота;

n – порядок фильтра.

При аппроксимации по Чебышеву:

,

где Т_n – полином Чебышева первого рода степени n;

ε – параметр, определяющий размах пульсаций в полосе пропускания

,

где α – максимально допустимое затухание в полосе пропускания.

При аппроксимации по инверсному Чебышеву:

,

где для ФНЧ и для ФВЧ;

ω₁ – начальная (для ФВЧ – конечная) частота полосы задержки.

.

3.Расчетная часть

3.1Расчет фильтра Баттерворта на основе МОС

Минимальный порядок фильтра равен:

.

Округляем до ближайшего большего целого n = 4.

Фильтр будет состоять из двух звеньев второго порядка с коэффициентами усиления К₁ = 4,58 и К₂=4,58.

Найдем нормированные значения коэффициентов нижних частот В, С. Они выбраны из таблицы. Коэффициент усиления звена 4,582575695.

В1=0,765367;В2=1,847759; С=1; К=4,58;

Выбираем номинальное значение емко­сти С₂ (предпочтительно близкое к значе­нию 10/f_c мкФ) и вычисляем значения сопротивлений.

мкФ=2,510^-10 Ф

Из условия, ёмкость: имеем:

Находим значения сопротивлений:

Выберем резистор R₂ из номинального ряда E192 = 187 кОм

Выберем резистор R₁ из ряда E192 равный 40,7 кОм

Выберем резистор R₃ из ряда E192 равный 51,7 кОм

Выбираем номинальное значение емко­сти

С₄= мкФ=2,510^-10ф

Из условия: имеем:

,

Находим значения сопротивлений: =

=

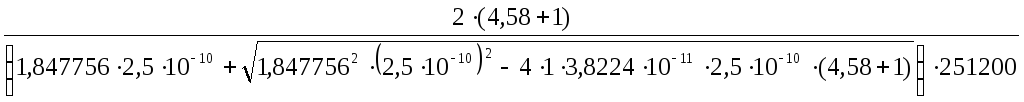=94195,43806 ОМ

Выберем резистор R₅ из ряда E192 равный 94,2 кОм

Выберем резистор R₄ из ряда E192 равный 21,0 кОм

=

=17605,76098 Ом

Выберем резистор R₆ из ряда E192 равный 17,6 кОм

Схема ФНЧ 4 порядка Баттерворта на МОС в Micro-Cap приведена ниже

3.2 Расчет фильтра Чебышева на основе МОС

Минимальный порядок фильтра равен:

2,455 =3

Округляем до ближайшего большего целого n = 3

Фильтр будет состоять из звена второго порядка с коэффициентом усиления К₁ =4,58 и звена первого порядка с К₂ = 4,58.

Найдем нормированные значения коэффициентов нижних частот В, С. Они выбраны из таблицы. С неравномерностью передачи 3.

В1=0,298620; С1=0,839174; С2=0,298620

Выбираем номинальное значение емко­сти С₂ (предпочтительно близкое к значе­нию 10/f_c мкФ) и вычисляем значения сопротивлений.

мкФ=2,510^-10 Ф

Выберем резистор R₂ из номинального ряда E192 равный 597 кОм

Выберем резистор R₁ из номинального ряда E192 равный 129 кОм

Выберем резистор R₃ из номинального ряда E192 равный 106 кОм

Выбираем номинальное значение емко­сти С₃ (предпочтительно близкое к значе­нию 10/f_c мкФ) и вычисляем значения сопротивлений.

мкФ=250 пФ

R₄==53324,8013

Выберем резистор R₄ из номинального ряда E192 равный 53,6 кОм

Схема ФНЧ Чебышева 3 порядка на МОС в Micro-Cap приведена ниже

4 Заключение

В ходе работы был произведен расчет активных фильтров низких частот: Баттерворта на основе МОС четвертого порядка и Чебышева на основе МОС треьего порядка, подобраны элементы для их построения.

Работа фильтров была смоделирована с помощью программного пакета MicroCAP.

Полученные графики АЧХ И ФЧХ фильтров соответствуют заданию и теоретическим положениям.

Список литературы

1. Баскаков С. И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000. – 462 с.

2. Джонсон Д. Справочник по активным фильтрам. – М.: Энергоатомиздат, 1983. – 128 с.

3. Разевиг В. Д. Система схемотехнического моделирования MicroCAP V. – М.: Солон.