1.Виды сигналов.Классиф-ция сигналов Сигнал-это фун-ия време-ни адекватная электричес-кой.1.реальные физ. про-цессы (тем-ра ,давлен.,и т.д)-это сигналы ,кот. пре-образ.в электр-е.2.фун-ия времени-мат.модель сигна-ла м.б. представ-на в виде граф-ка,табл. или анал-го выр-я.Классиф-я сигна-лов:1.детерминированный –сигналы знач-я кот. в любой момент времени полностью известно, т.е. предсказуем-ть с вероят-ю =1.Принято различать следующие детерм. сигна-лы: а).управлеющие (ин-форм-ии не несет)-аналит-е (непрерывные) явл.фун-ей времени,повтор-е з-н изме-нения физ. величины.б). В.Ч.немодулир-е по-след-ть импульсов , ампли-туды кот.соответ-т знач-ю физ. вел. в дискрет. момен-ты времени,это В.Ч. колеб-я кот способны распростр. э/м волны на большие расст-я. в). модулире (не-сут информацию)-дискрет-ные по времени и кван-тован-е по уровню сигналы амплитуды кот. м. прини-мать только ограни-ченное число фиксир-х значений ,эти послед-ти представ. цифр-ми кодами,наз-т циф-ровыми сигналами.В.Ч. ко-лебания один или неск-ко пар-ров кот. промодули-рован колеба-ми управл. сигнала и распростр. в виде э/м волн.2.случайный-сигнал знач-я кот.в любой момент времени пред-сказать невозможно с вероят-ю=1. Все сиг-налы несущие информа-цию явл. случ-ми,а полностью де-термин-й сигнал инфор-мации не содержит,-т.к. м. создаваться в месте приема без канала связи.

2.Элементы теории сиг-налов.Подразделенияе по диапазонам частот.Особенности распростронения. Изменяющийся во времени физический процесс, отражающий передаваемое сообщение называется сигналом . Для выбора того или иного диапазона зависит от фактороф:1)Особ-ти распр-я ЭМволн данного диап-а и вля-е врм-и года,суток,солн.радиации...2)техн-е воз-ти:направленность и размеры антенн-й сис.3)характера шумов и помех4)ширины спктра.Подр. по диап-м:сверхдлинные,длин-е,ср-е,корткие,метровые,Дм-е... Диап-н измер-й огран-ся max и min значениями диапазона.Сцелью повыш-я точности измер-й диапазон измер-й средства измер-й м.б. разбит на несколько поддиапаз-в.При переходе с одного поддиап-на на другой некотор. составл. основной погреш-ти уменьш-ся,что приводит к повышению точности измер-й.

3.Терия инф-ции, ви-ды сообщ-ий.Понятие меры. Важней-шим вопросом теории инф-ции явл. установ-е меры кол-ва и кач-ва инфор-ции .Инфор-е сигналы меры отвечают 3-м основным направ-ям:структ-му , статич-му и сематич-му.Струк-я теория -рассматр. диркет-е строение массиов инф-ции и их измерение простым подсчетом ин-формац-х э-тов или комбинат-м методом предлаг-ее простейшее кодир-е массивов инф-ии. Под сооб-ем понимают совок-сть знаков или первичных сигналов содержащих инф-ию. Иначе говоря, сообщение - это информация представленная в какой-либо форме. Пример сообщ-й: текст телеграммы, данные на выходе ЭВМ, речь, музыка и т.д. Статичес-я теория оперир-т понятием энтропия как мера неопред-ти учит-я вероят-ть появления,а след-но информатив-ть тех или иных сообщен. Сематическая теория –учит-т целесообр-ть ,цен-ность,полез-ть или сущест-ть инф-ции.Источ-к инф-ции и создаваем. ими сообщен. раздел-ся на дис-кретные и непрерыв-е.Дискр-е –складыв-ся из множ-ва элем-в создаваемого источника послед-го во времени .Дискрет-й источник в конечное время созд-т конеч-е множ-во сообщен.(текст,послед-ть и т.д.)2. непрер-е –отражен-е какой-либо физ.вел. измен-ся в зад-ом интервале времени ,получ-е коенеч-го множ-ва сообщен. за конеч-й промеж-к времени достиг-ся путем дискретиз-и во времени и квантованием по уровню.

4.Струк-ные меры инф-ции .Кванты.Биты. Струк-е меры учитыв-т только дискрет-е строение данного инфор-го комплекса в данном случ-е кол-во содержащ-ся инфор-ии ,связями м/у ними или комбинациями.Информац-й элем-т-неделимые частицы-кванты инфор-ии.В струк-й теории различ-т геометр-ю,комбинат-ю и аддит-е меры (мера Хартли)инфор-ии.Ед-ца измер-я кол-ва инфор-ии в данном случ-е –биты.Геометр-я мера-сводится к измер-ю длины или площ-ди ,или объема геометр. Модели данного инфор-го комплекса. Геометр-м методом опред. Потенциал-я энергия,т.е.максим-но возмож-е кол-во инф-ции задан-е в структур-х габаритах.Кол-вом инф-ии будем наз-ть инф-ую емкость исслед-ой информац-й сис-мы.

m_X =x/Δx ;m_t=t/Δt; m_n=n/Δn; m- кол-во инф-ии в квантах.Если дискрет-е отсчеты по x,n и t осущ-ся ч/з интервалы Δx,Δn,Δt,то непрер-е коорди-наты распад-ся на элем-ты,т.е. кванты M=m_xm_tm_n К комбинаторной мере целесообразно прибегать тогда,когда треб-ся оценить возм-ть передачи инфор-ии при помощи разл-х комбин-й и элем-в,образ-е комбинац-й будет одной из форм кодир-я инфор-ии . Кол-во инфор-ии вычисл-ся как кол-во комбин-й элемен-в ,т.о. оценке подвергается комбинатор-е сво-во потенциал-го структ-го разнообр-я.Элем-ты счит-ся неодинаковыми ,если отл-ся любым признаком:размерами,цветом,формой и т.д. Квантование сигнала-преобразование сигнала в последовательность импульсов (квантование сигнала по времени) или в сигнал со ступенчатым изменением амплитуды (квантование сигнала по уровню), а также одновременно и по времени, и по уровню.

БИТ (англ. bit, от binary — двоичный и digit — знак), двоичная еди-ница, в теории информации еди-ница количества инфор-мации. Бит в вычисли-тельной технике — двоичная цифра, двоичный разряд. Число бит памяти ЭВМ определяет максимальное количество двоичных цифр, вмещаемых ею; число бит данных есть количество двоичных разрядов, в которых они записаны.

5.Аддитивная мера (Хартли). Втеории инф-ии важн-ю роль играет комбинаторика чисел и кодов.

Эта мера предложена в 1928 году американским ученым Хартли, поэтому имеет второе название – мера Хартли. Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита: I = l log h, где I – количество информации, содержащейся в сообщении; l – длина сообщения; h – мощность исходного алфавита. При исходном алфавите {0,1}; l = 1; h = 2 и основании логарифма, равном 2, имеем I = 1*log₂2 = 1.

Данная формула даёт аналитическое определение бита (BIT - BInary digiT) по Хартли: это количество информации, которое содержится в двоичной цифре.

Единицей измерения информации в аддитивной мере является бит.

6.Статистические меры информации. Вероятность и информ-ия. Статистическое направление оперирует понятием энтропии как меры неопределенности, то есть здесь учитывается вероятность появления тех или иных сообщений. Под информацией обычно понимают совокупность сведений об окружающем мире являющихся объектом хранения, передачи и преобразования. . Информация, основанная на однозначной связи знаков или сигналов с объектами реального мира, называется семантической или смысловой. Информация, заключенная в характере (порядке и взаимосвязи) следования знаков сообщающей называется синтаксической.

При вероят-м подходе инф-я рассм-ся как сообщ-е об исходе случ-х событ-й,реализ-я случ-х величин и фун-й о кол-ве инфор-ии ставит-ся в завис-ть от вероят-ти этих событий величин и фун-й . Определения кол-ва инф-ии явл. случ.вел-й, поск-ку сами сообщ-я явл. случ-ми. В такой ситуации количество информации, содержащееся в одном дискретном сообщении u_k целесообразно определить как функцию вероятности появления этого сообщения P(u_k) и характеризовать величиной Знак минус в равенстве необходим для того, чтобы количество информациибыло неотрицательным числом т.к. всегда

7.Понятие энтропии.Энтропия ансамбля.

. Неопред-ть в каждой ситуации хар-ся вел-й наз-ой энтропией.

H=-1/N*(_I=1E^K n_i*ln(n_i/N)

N-общее кол-во мол-л,n-кол-во мол-л со скоростью V+ΔV; n_i/N=p_i;

H= -(_I=1Е^k p_i *ln p_i);

H=-1,44*(_i=1E^k p_i*log₂p_i)-энтропия ансампбля.Ансамбль-полная группа событий или поле несовместных событий с извес-м распред-м вероят-й(p=1).Энтропия ансамбляы-кол-я мера его неопред-ти или информат-ти.

Пусть имеется N возможных исходов опыта.Из них k-разных,и i-исход. повтор-ся n_i раз ,то сред-е кол-во инфор-ии:I_СР.=(n₁I₁+n₂I₂+...+n_KI_K)/N;

Кол-во инфор-ии отдел-го события:

I_i=log₂(1/p_i)=-log₂p_i;p=n_i /N;I_СР=-(_i=1E^k p_i*log₂p_i);H=I_СР[бит]

Для натур-го логарифма ед-цы измер-я-1Нит.Для десятичного-1Дит. 1Нит.=1,44 бит;1Дит.=3,3219 бит.Энтропия м.б. определена как среднее кол-во инфор-ии на одно сообщен-еили мат. ожид-екол-ва инфор-ии для измер-й вх-й вел-ны х. H(x)=M[I(x)];Требованияы для фун-ии H(p):1)H(p)-непрерывна на интервале 0<=p_i>=1.т.е. при малых измен-х p велич.энтропии мало измен-ся.2)p(H)симметр-но отн-но р ,т.е. не измен-ся при любомй перемене мест аргумента p_i ;3)H(p₁,p₂,...p_k-1 ,q1,q2) =H(p₁,p₂...,q₁)+H(p₁,p₂...,q₂)

8.Свойства энтропии.

1).Энтропия всегда неотриц-на,т.к. знач-е вероят-й выраж-ся дроб-ми велич-ми,так что члены у нас неотриц-ны: log₂p_i=-(-Q_i); 2).Энтропия=0,в том случае,когда одно событ.=1,а остал-е=0;3).Энтропия имеет max знач-е в том случае,когда все вероят-ти равны м/у собой. H=-log₂(1/k);p1=p2=..=-pk=1/k Логарифм.и стат-я инф-ия совпад. с аддит-й мерой Хартли.H=I’=log₂h

Max H=1,p=0.5, когда 2 состояния равновероятны.при р=0 или р=1 ,Н=0, что соотв-т полной невозм-ти ,или полной достовер-ти события.

9, Энтропия объединения. Условная,безусловная,взаимная, совместная.Объед-ние-совок-ть 2-х и более взаимосвяз-х ансамблей дискретных случ-х переем-х.

ОбъединениеХУ:

Вероят-ть произвед-я совместных завис-й событий х и у = произв-ю безусловн-х вероят-й. р(х) или р(у)на условные вероят-ти р(у/х) или р(х/у):р(у/х)=р(х,у)/р(х); р(х/у)=р(у,х)/р(у);

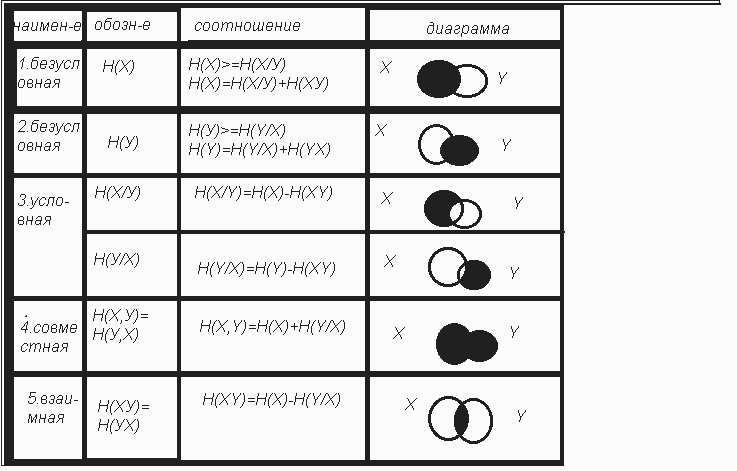
Схема передачи дискретной инф-иипо каналу связи.Н(х),Н(у)-безусл-е энтропии источ-ка и прием-ка.(сред-ее кол-во инф-ии на символ подав-й ист-ком /прием-ком);Н(у/х),Н(х/у)-услоная энтропия у относ-но х или мера кол-ва инф-ии в приемнике,когда известно что перед-ся х.Н(х,у)-взаимная энтропия сис-мы передачи/ приема в целом или средняя инф-ия за пару перед-го или прин-го сигнала.Если в сис-ме нет потерь и искажений ,то условн. энтропия=0,а кол-во взаим-й инф-ии = энтропии ,либо ист-ка,либо прием-ка.

I(x,y)= H(x,y)=H(x)=H(y);

10. Кол-во информации и избыточность.Тезаурус. Если неопред-ть сним-ся полностью,то инфор-ия I=H;

В случ-е неполного разреш-я имеет место част-я ,инфор-ия явл-ся разностью м/у нач-й и конеч-й энтроп-й.Max кол-во инф-ии получ-ся тогда,когда полностью снимается неопред-сть,причем эта неопред-сть была наиболее вероятн. Всех событий ,если они были одинаковы.

I’=- log p = Hmax

Абсолютная избыт-ть инфор-ии:

D абс представл. собой разнгость м/у возможным кол-м инф-ии и энтропии.

Dабс.=I’-H;

Dабс.=(Hmax-H)/Hmax=1-H/Hmax

Энтропия, шум,тезаурус. Под понятием тезаурус ,запас знаний или словарь ,испол-мый приемником инф-ии.

СИС-МА Sx(объект,ист-к,ответ язык х, структура ,энтропия ,семантика)соответ-т сис-ме Sy(субъект,приемник,запрос,язык у,композиция, тезаурус,прогматика);схемы извлечения передачи и приема информации с учетом Н,n.Q

Ист-к(H-H2=I_Q)отдано в канал(I_Q-I_Ω)потеря на шум N,в приемник воспринято(I-Q)

I_Q=H1-H2 поступает в канал ,где часть инф-ии мен-ся ,искаж-ся шумом N.Оставш-ся часть информ-ии I достигает прием-ка и восприн-ся в той степени в какой позволяет тезаурус.Если тезаурус неадекватен перед-ой инф-ии (очень мал или вообще отсутств.),то самая новая и полезная инф-ия не воспринимается в след-ии того что она не будет принята прием-ком с приемом новой инф-ии тезаурус может у величиться.