
SopromatGafarov
.pdf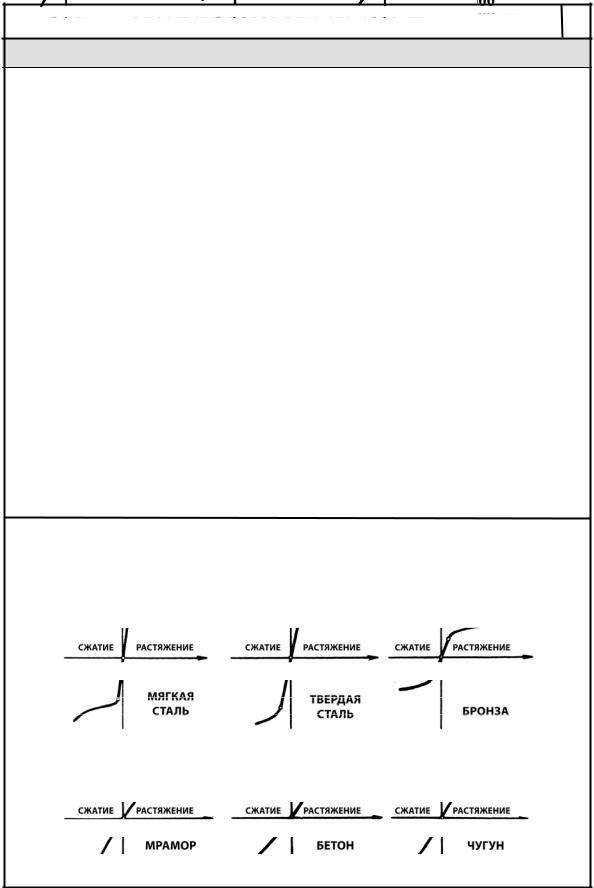
ИЛЛЮСТРАЦИИ К ТЕМЕ «РАСТЯЖЕНИЕ И СЖАТИЕ» |
2 |
3.МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
3.1.Диаграммы растяжения различных материалов
3.2. Диаграммы растяжения и сжатия
55
ИЛЛЮСТРАЦИИ К ТЕМЕ «РАСТЯЖЕНИЕ И СЖАТИЕ» |
2 |
4.П Р И М Е Р Ы Р А С Ч Е Т О В
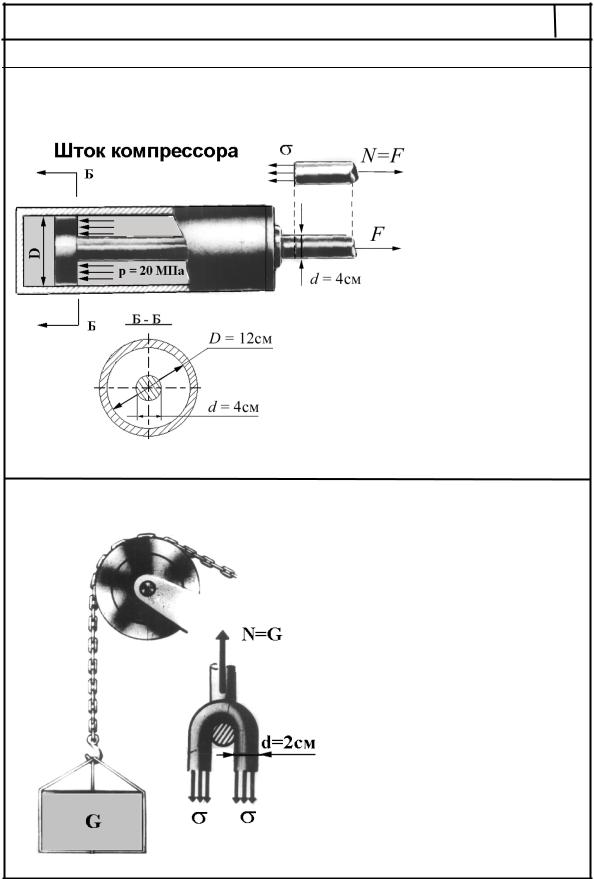
4.1.Проверка прочности
Сила, растягивающая шток
F = p π4 (D2-d2) = 200кН.
Площадь поперечного сечения
A= πd2/4= π 42/4=
=12,56 см2.
Допускаемое
напряжение
[σ] = 180МПа.
Фактическое
напряжение
σ = N/A = 162,5 МПа.
4.2. Определение допускаемой нагрузки
Допускаемое напряжение
[σ]=100МПа.
Площадь поперечного сечения
A= 2πd2/4=6,28 см2.
Допускаемая нагрузка
[G] = [N] = [σ] A= 62,8 кН.
56
3.ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ
ИГИПОТЕЗЫ ПРОЧНОСТИ
Число есть сущность всех вещей.
П и ф а г о р
3.1. О Б Щ И Е С В Е Д Е Н И Я
Напряжение в точке, равное
p = lim ( R / A) , |
(3.1) |
A→0 |
|
зависит от ориентации площадки. Каждой площадке с нормалью ni соответст-
вует свой вектор напряжения pi . Совокупность векторов напряже-
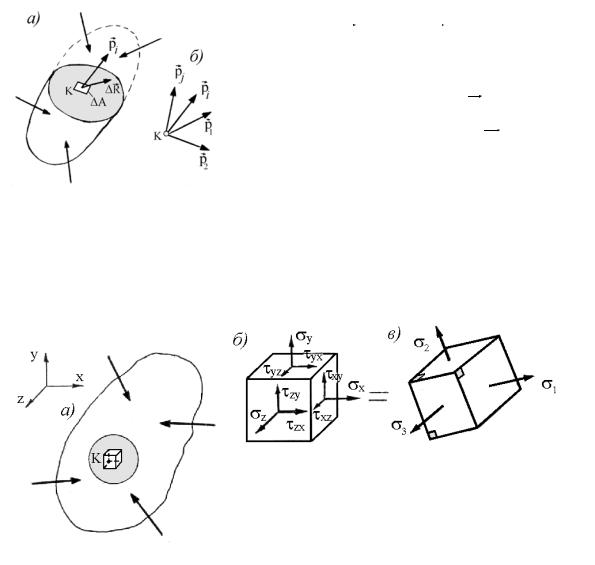
Рис. 3.1 ний для всевозможных площадок, проходящих через данную точку, представ-
ляет напряженное состояние в этой точке. Итак, если напряжение – это одиночный вектор, то напряженное состояние – пучок векторов
(рис. 3.1, б).
Tн = |
σx |
τxy |
τxz |
|
σ1 |
0 |
0 |
|
|
|
(3.2) |
|
|
|
|||||||||
τyx |
σy |
τyz |
= |
0 |
σ2 |
0 |
|
|
|
||
|
τzx |
τzy |
σz |
|
0 |
0 |
σ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.2
57
Количественной характеристикой напряженного состояния выступает тензор напряжения Tн, компонентами которого являются нормальные и касательные напряжения на трех взаимно перпендикулярных площадках (рис. 3.2).
Здесь σx, σy, σz – нормальные напряжения; τxy, τyz, τzx – касательные напряжения (первый индекс означает нормаль к площадке, а
второй – параллельную касательному напряжению ось). |
|
Касательные напряжения |
подчиня- |
ются закону парности, согласно которому |
|
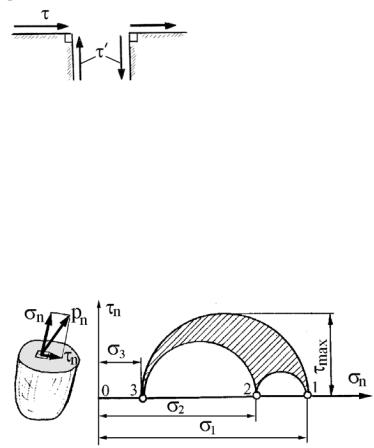
τ = τ′ или в общем виде τij = τji. |
(3.3) |
В каждой точке тела существуют, по крайней мере, три взаимно перпендикулярные площадки, свободные от касательных напряжений и называемые главными (рис. 3.2, в). Действующие на них главные напряжения обладают экстремальными свойствами и связаны между собой
соотношением σ1 ≥ σ2 ≥ σ3 (с учетом знака !) (3.4)
Напряженное состояние в точке можно изобразить графически с помощью круговой диаграммы Мора. Геометрическим образом напряженного состояния является криволинейный тре-
угольник 123. Из Рис. 3.3 рис. 3.3 наглядно
видно, что наибольшее касательное напряжение равно
τmax = 0,5(σ1 −σ3 ). |
(3.5) |
Классификация напряженных состояний:
1.О б ъ е м н о е (все три главных напряжения отличны от нуля).
2.П л о с к о е (одно из главных напряжений равно нулю).
3.Л и н е й н о е (два главных напряжения равны нулю).
58

3.2. ЛИНЕЙНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
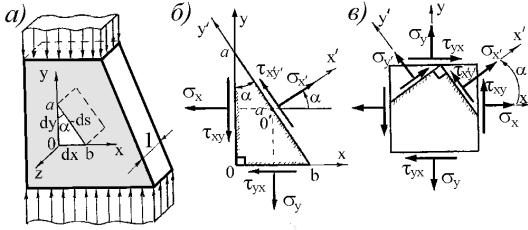
Рис. 3.4
Оно реализуется при центральном растяжении и сжатии прямолинейного стержня (рис. 3.4, а). Для определения напряжений на произвольной наклонной площадке выделим элемент и рассмотрим его равновесие:
|
∑Fin = 0 , |
σα Aα = σz Acos α, |
|
|
откуда |
σα = σz cos2 α; |
|
||
|
∑Fit |
= 0, |
τα Aα = σz Asin α, |
|
откуда |
τα = σz sin αcos α = 0,5σz sin 2α. |
|
||
Итак, |
σα |
= 0,5σz (1 + cos 2α), |
(3.6) |
|
|
τα = 0,5σz sin 2α. |
|||
|
|
|||
На площадке, перпендикулярной к данной, с нормалью, накло- |
||||
ненной к оси z |
под углом |
β= −(90° − α) |
|
|
|
|
|
σβ = σz sin 2 α, |
(3.7) |
|
|
|
τβ = −0,5σz sin 2α . |
|
|
|
|
|
|
Из формул (3.6) и (3.7) вытекают следующие выводы: |
|
|||
1. Наибольшее нормальное напряжение возникает в попереч- |
||||
ном сечении стержня |
|
σmax = σα=0 = σz = Nz / A. |
|
|
59
2. Наибольшее касательное напряжение возникает на площад-
ке, наклоненной под углом 45° к оси стержня |
|
τmax = τα=45D |
= 0,5σz . |
|||||||
3. На двух любых взаимно перпендикулярных площадках каса- |
||||||||||
тельные напряжения равны по величине |
|
τα |
|
= |
|
τβ |
|
, а сумма нормаль- |
||
|
|
|
|
|||||||
|
|
|||||||||
ных напряжений постоянна |
σα + σβ = σz = const . |
|
||||||||
Исключая из формул (3.6) угол α, получим |
|
|||||||||
(σα − 0,5σz )2 + τα2 |
= (0,5σz )2 . |
(3.8) |
||||||||
Это уравнение круговой диаграммы Мора для линейного напряженного состояния (рис. 3.4, в).
Линейная деформация в произвольном направлении, образующем угол α с осью z, определяется по закону Гука следующим выра-
жением: |
|
|
σz (cos2 |
|
|
|
εα = |
1 |
(σα − νσβ) = |
α − νsin 2 α) . |
(3.9) |
||
E |
||||||
|
|
E |
|
|
3.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Рис. 3.5
Оно реализуется, например, в тонкой пластине, нагруженной по контуру силами, равномерно распределенными по ее толщине
(рис. 3.5). 60
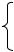
Зная напряжения на площадках, совпадающих с координатными плоскостями xz и yz, определим напряжения на произвольной наклонной площадке, а также наибольшие нормальные и касательные напряжения, возникающие в данной точке. Выделим из пластины бесконечно малый элемент aob и рассмотрим его равновесие:
∑mo′ = 0 , τxy dy 1 dx / 2 = τyx dx 1 dy / 2 , откуда τxy = τyx ; (3.10)
∑Xi′ = 0 ,
σx′ds 1 − σx dy cos α − σy dx sin α − τxy dy sin α − τyx dx cos α = 0 ,
откуда после сокращения на ds
σx′ = σx cos2 α + σy sin 2 α + τxy sin 2α; (а) ∑Yi′ = 0, τx′y′ds + σxdysin α − σy dxcosα − τxydy cosα + τyxdxsin α = 0 ,
откуда после упрощения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ ′ ′ = −0,5(σ |
x |
− σ |
y |
)sin 2α + τ |
xy |
cos 2α. |
(б) |
||||||
|
x y |
|
|
|
|
|
|
|
|
|
|
|||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σx′ |
= 0,5(σx + σy ) + 0,5(σx − σy ) cos 2α + τxy sin 2α, |
(3.11) |
||||||||||||
τ ′ |
′ = −0,5(σ |
x |
− σ |
y |
)sin 2α + τ |
xy |
cos 2α. |
|||||||
x y |
|
|
|
|
|
|
|
|
|
|
|
|||
Если заменить в формуле (а) угол α на 90° + α, то получим |
||||||||||||||
σy′ = σx sin 2 α + σy cos2 α − τxy sin 2α. |
(в) |
|||||||||||||
Исключая в формулах (3.11) угол α, получим уравнение круговой диаграммы Мора для плоского напряженного состояния (рис. 3.6)
[σ |
x |
′ − 0,5(σ |
x |
+ σ |
y |
)]2 |
+ τ2′ |
′ =[0,5(σ |
x |
− σ |
y |
)]2 |
+ τ2 . |
(3.12) |
|
|
|
|
|
|
x y |
|
|
|
xy |
|
|||||
Это уравнение типа |
|
|
|
(x − a)2 + y2 = R2 , |
|
|
|||||||||
где |
|
a = 0,5(σx + σy ) , |
|
R2 =[0,5(σx − σy )]2 + τ2xy . |
|
||||||||||
61

|
|
Непосредственно |
из |
|
круговой |
|
|
диаграммы находим величины глав- |
|||
|
|
ных напряжений: |
|
|
|
|
|
σmax = a ± R = 0,5[ (σx − σy ) ± |
|||
|
|
min |
|
|
(3.13) |
|
|
± (σx − σy )2 + 4τ2xy ] . |
|||
|
|
|
|||
Рис. 3.6 |
|
Ориентация главных |
осей оп- |
||
|
|
ределяется из условия |
τ |
|
′ ′ = 0 , |
|
|
|
|
x y |
|
откуда |
tg2α0 = 2τxy /(σx − σy ) . |
|
|
(3.14) |
|
Более удобна следующая формула: |
|
|
|
||
|
tgαmax = (σmax − σx ) / τxy . |
|
|
(3.15) |
|
|
min |
min |
|
|
|
Экстремальные касательные напряжения равны по величине радиусу круговой диаграммы
τmax = ±R = ±0,5 (σx − σy )2 + 4τ2xy |
(3.16) |
min |
|
и действуют на площадках, равнонаклоненных к главным осям.
Частный случай – чистый сдвиг (рис. 3.7) |
|
|
Так как σx = σy = 0, |
τxy = τyx = τ, то по формулам (3.13) и (3.14) |
|
|
получим |
|
|
σmax = ±τ, |
|
|
min |
|
|
следовательно, |
|
|
σ1 = +τ, σ2 = 0 , σ3 = −τ; |
|
|
tg2α0 = ±∞ , |
откуда |
Рис. 3.7 |
2α0 = ±90° и |
α0 = ±45°. |
62

Зависимости между напряжениями и деформациями определяются законом Гука:
• п р я м а я ф о р м а
εx = (σx − νσy ) / E , |
γxy = τxy / G ; |
(3.17) |
|
εy = (σy − νσx ) / E , |
|||
|
|
||
• о б р а т н а я ф о р м а |
|
|
|
σx = E(εx + νεy ) /(1 − ν2 ) , |
τxy = Gγxy . |
(3.18) |
|
|
σy = E(εy + νεx ) /(1 − ν2 ) ,
3.4.ЗАВИСИМОСТИ МЕЖДУ НАПРЯЖЕНИЯМИ
ИДЕФОРМАЦИЯМИ
Для установления зависимостей напряжений и деформаций от внешних сил, нагружающих тело, необходимо знать связь между напряжениями и деформациями в общем случае напряженного состояния. С целью получения искомых аналитических выражений воспользуемся принципом независимости действия сил и законом Гука при простом растяжении. Начнем со случая трехосного растяжения.
Закон Гука в главных осях. Рассмотрим элемент, вырезанный из тела и имеющий форму параллелепипеда, ребра которого направ-
лены по главным осям (рис. 3.8). Относитель- |
|
ное удлинение в направлении оси 1, обуслов- |
|
ленное напряжением σ1, равно σ1/Е. Напря- |
|
жениям σ2 и σ3 |
соответствуют удлинения по |
оси 1 обратного |
знака, равные − νσ2 / E и |
− νσ3 / E . Складывая, получим |
|
|
ε1 = σ1 / E − νσ2 / E − νσ3 |
/ E . |
Рис. 3.8 |
|
|
63

Такие же выражения получаются по аналогии для ε2 и ε3.
|
ε = |
1 |
[σ − ν(σ |
2 |
+ σ |
|
)], |
|
||||||||
|
|
|
|
|
||||||||||||
|
1 |
|
E |
1 |
|
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В итоге |
ε |
2 |
= |
1 |
|
|
[σ |
2 |
− ν(σ |
3 |
+ σ )], |
(3.19) |
||||
|
|
|
|
|||||||||||||
|
|
|
|
E |
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ε |
3 |
= |
|
1 |
[σ |
3 |
− ν(σ + σ |
2 |
)] . |
|
|||||
|
|
|
|
|||||||||||||
|
|
|
|
E |
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Объемная деформация. Упругая деформация вообще сопровождается изменением объема. Так, объем изображенного на рис. 3.8
параллелепипеда до деформации равен |
V0 |
= abc . В результате де- |
||
формации ребра параллелепипеда стали |
|
|
|
|
a + a = a(1 + ε1) , |
b + b = b(1 + ε2 ) , |
c + c = c(1 + ε3 ) |
|
|
и новый объем V1 = (a + |
a)(b + b)(c + |
c) = abc(1 + ε1)(1 + ε2 )(1 + ε3 ) . |
||
Следовательно, относительное изменение объема равно |
|
|||
εV = (V1 −V0 ) /V0 = (1 + ε1)(1 + ε2 )(1 + ε3 ) . |
(3.20) |
|||
Поскольку деформации малы по сравнению с единицей, то, выполняя перемножение трех скобок в правой части (3.20), мы сохраним только первые степени деформаций, отбросив их произведения (члены второго и третьего порядка малости). Таким образом, для малых деформаций
|
|
εV = ε1 + ε2 + ε3 . |
(3.21) |
|||||
Желая связать относительное изменение объема с напряжения- |
||||||||
ми, сложим три уравнения (3.19). Получим: |
|
|
|
|||||
ε |
= |
1 |
(σ + σ |
2 |
+ σ |
3 |
)(1 − 2ν) , |
|
|
||||||||
V |
|
E |
1 |
|
|
|
||
|
|
εV = σ/ K , |
|
|||||
или в компактной форме |
|
|
(3.22) |
|||||
где σ = (σ1 + σ2 + σ3 ) / 3 |
– среднее напряжение, |
K – модуль объем- |
||||||
ной деформации, равный |
|
|
K = E /[3(1 − 2ν)] . |
|
||||
При положительном σ величина εV должна быть также положительной, при отрицательном σ – отрицательной. Это возможно только
64
