
graph
.pdf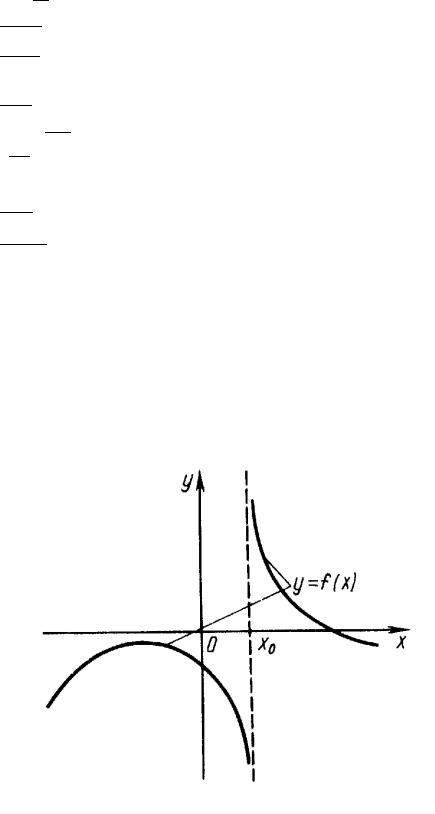
x3. €á¨¬¯â®âë |
11 |
25.y = 2 jxxj;
26.y = 1+211=x ;
27.y = 2xj3x x12j;
28.y = tgx;
29.y = 4 4x2 ;
30.y = arctg x+22 ;
1
31. y = 2x 2 ;
1
32. y = 1 2x ;
33. y = x23j+xjx ; 34. y = j44x xx23j.
x3. €á¨¬¯â®âë
3.1. •®-ï⨥ ᨬ¯â®âë
•àï¬ ï x = x0 - §ë¢ ¥âáï ¢¥à⨪ «ì-®© |
ᨬ¯â®â®© £à 䨪 äã-ªæ¨¨ |
|
y = f (x), ¥á«¨ å®âï ¡ë ®¤¨- ¨§ ¯à¥¤¥«®¢ x limx0+ f (x) ¨«¨ x limx0 |
f (x) à ¢¥- +1 |
|
! |
! |
|
¨«¨ 1.
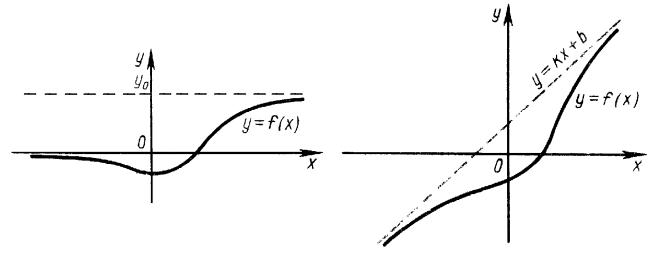
•àï¬ ï y = kx + b - §ë¢ ¥âáï - ª«®--®© ᨬ¯â®â®© £à 䨪 äã-ªæ¨¨
y = f (x) ¯à¨ x ! 1, ¥á«¨ lim (f (x) (kx + b)) = 0.
x!1
•à¨ k = 0 - ª«®-- ï ᨬ¯â®â - §ë¢ ¥âáï £®à¨§®-â «ì-®©.
€- «®£¨з-® ®¯а¥¤¥«повбп б¨¬¯в®вл ¯а¨ x ! 1 ¨ ¯а¨ x ! +1.
12 |
x3. €á¨¬¯â®âë |
•àï¬ ï y = kx + b - §ë¢ ¥âáï |
ᨬ¯â®â®© £à 䨪 |
||||||
¯à¨ x ! 1, ¥á«¨ x lim (f (x) (kx + b)) = 0. |
|||||||
|
|
|
! 1 |
|
|
|
|
•àï¬ ï y = kx + b - §ë¢ ¥âáï |
ᨬ¯â®â®© £à 䨪 |
||||||
¯à¨ |
x |
! +1, ¥á«¨ x |
lim (f (x) |
|
(kx + b)) = 0. |
||
|
+ |
1 |
|
|
|||
|
|
|
! |
|
|
|
|
äã-ªæ¨¨ y = f (x)
äã-ªæ¨¨ y = f (x)
•à¨¬¥à 1. • ©â¨ |
|
ᨬ¯â®âë £à 䨪 |
|
äã-ªæ¨¨ y = 4 + 1. |
|||||||||||||||||||
•¥è¥-¨¥. • 室¨¬: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
|
|
xlim 4 + x |
= 4; |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯®í⮬ã y = 4 | £®à¨§®-â «ì- ï |
ᨬ¯â®â £à 䨪 |
|
¤ --®© äã-ªæ¨¨. „ - |
||||||||||||||||||||
«¥¥, â ª ª ª |
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
x |
|
|
1 |
|
||
x 0+ |
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|||||||||||
lim |
4 + |
1 |
= + |
|
; |
|
lim |
4 + |
1 |
|
|
= |
|
; |
|||||||||
|
|
|
|
|
|
||||||||||||||||||
|
! |
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|||
â® x = 0 | ¢¥à⨪ «ì- ï |
ᨬ¯â®â . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
•à¨¬¥à 2. • ©â¨ |
|
ᨬ¯â®âë £à 䨪 |
|
äã-ªæ¨¨ y = 2 x. |
|||||||||||||||||||
•¥è¥-¨¥. ’ ª ª ª |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
lim |
2 x = 0: |
x |
lim |
|
2 x = + |
1 |
; |
|
|
|||||||||||
|
|
! |
+ |
1 |
|
|
! 1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
â® ®áì ¡áæ¨áá (¯àï¬ ï y = 0) ï¥âáï £®à¨§®-â «ì-®© |
ᨬ¯â®â®© £à 䨪 |
||||||||||||||||||||||
¤ --®© äã-ªæ¨¨ ¯à¨ x ! +1. ‚¥à⨪ «ì-ëå |
ᨬ¯â®â -1¥â. |
||||||||||||||||||||||
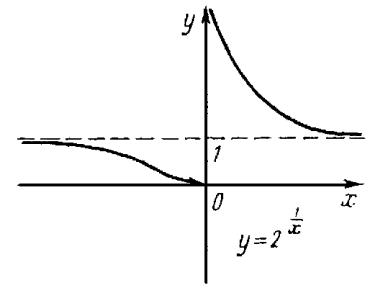
•à¨¬¥à 3. • ©â¨ |
|
ᨬ¯â®âë £à 䨪 |
|
äã-ªæ¨¨ y = 2x . |
|
||||||||||||||||||
•¥è¥-¨¥. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= 1; |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
lim 2x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x!1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
§- ç¨â, y = 1 | £®à¨§®-â «ì- ï |
ᨬ¯â®â £à 䨪 |
|
äã-ªæ¨¨ y = 2x . Žáì |
||||||||||||||||||||
®à¤¨- â (¯àï¬ ï x = 0) ï¥âáï ¢¥à⨪ «ì-®© |
ᨬ¯â®â®©, â ª ª ª |
||||||||||||||||||||||
|
|
|
lim 2x = +1; |
lim 2x |
= 0 |
|
: |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x!0+ x!0
x3. €á¨¬¯â®âë |
13 |
•à¨¬¥à 4. • ©â¨ |
ᨬ¯â®âë £à 䨪 äã-ªæ¨¨ y = |
sinx |
. |
|
|||
|
|
||||||
|
|
|
|
|
x |
|
|
•¥è¥-¨¥. ’®çª |
x = 0 ï¥âáï â®çª®© à §àë¢ ¯¥à¢®£® த |
(á¬. |
|||||
¯à¨¬¥à 3 x2), ¯®í⮬㠢¥à⨪ «ì-ëå |
ᨬ¯â®â -¥â. ƒ®à¨§®-â «ì-®© |
ᨬ- |
|||||
|
sinx |
= 0. • ª«®--ëå ᨬ¯â®â |
|||||
¯â®â®© ï¥âáï ¯àï¬ ï y = 0, â ª ª ª lim |
x |
||||||
-¥â. |
|
x!1 |
|
|
|
|
|
‡ ¬¥ç -¨¥. €á¨¬¯â®â £à 䨪 äã-ªæ¨¨ ¬®¦¥â ¯¥à¥á¥ª âìá ¬ £à 䨪 äã-ªæ¨¨. •®«¥¥ ⮣®, ᨬ¯â®â £à 䨪 äã-ªæ¨¨ ¬®¦¥â ¡¥áª®-¥ç-®¥ ç¨á«® à § ¯¥à¥á¥ª âì á ¬ £à 䨪 äã-ªæ¨¨ (á¬. ¯à¨¬¥à 4).
3.2. • 宦¤¥-¨¥ £®à¨§®-â «ì-ëå ¨ - ª«®--ëå ᨬ¯â®â
ƒ®à¨§®-â «ì-ë¥ ¨ - ª«®--ë¥ á¨¬¯â®âë £à 䨪 äã-ªæ¨¨ y = f (x) ¯à¨ x ! 1 ¬®¦-® - 室¨âì ¯® á«¥¤ãî饬㠫£®à¨â¬ã.
1. |
‚ëç¨á«¨âì lim f (x). …᫨ íâ®â ¯à¥¤¥« áãé¥áâ¢ã¥â ¨ à ¢¥- -¥ª®â®- |
||||
|
|
|
x!1 |
|
|
|
஬ã ç¨á«ã b, â® y = b | £®à¨§®-â «ì- ï ᨬ¯â®â . …᫨ ¯à¥¤¥« -¥ |
||||
|
áãé¥áâ¢ã¥â ¨«¨ à ¢¥- ¡¥áª®-¥ç-®áâ¨, â® ¯¥à¥©â¨ ª® ¢â®à®¬ã ¯ã-ªâã. |
||||
2. |
‚ëç¨á«¨âì lim |
f (x) |
. …᫨ íâ®â ¯à¥¤¥« -¥ áãé¥áâ¢ã¥â ¨«¨ à ¢¥- ¡¥á- |
||
|
|||||
|
|
|
x!1 |
x |
|
|
ª®-¥ç-®áâ¨, â® |
ᨬ¯â®âë -¥â. …᫨ áãé¥áâ¢ã¥â ª®-¥ç-ë© ¯à¥¤¥« |
|||
|
lim |
f (x) |
= k, â® ¯¥à¥©â¨ ª âà¥â쥬ã è £ã. |
||
|
|
||||
|
x!1 |
x |
|
|
|
3. |
‚ëç¨á«¨âì xlim (f (x) kx). …᫨ íâ®â ¯à¥¤¥« -¥ áãé¥áâ¢ã¥â ¨«¨ à - |
||||
|
|
!1 |
|
|
|
|
¢¥- ¡¥áª®-¥ç-®áâ¨, ⮠ᨬ¯â®âë -¥â. …᫨ áãé¥áâ¢ã¥â ª®-¥ç-ë© |
||||
|
¯à¥¤¥« xlim (f (x) kx) = b, â® ¯¥à¥©â¨ ª ç¥â¢ñà⮬ã è £ã. |
||||
|
|
!1 |
|
|
|
4. |
‡ ¯¨á âì ãà ¢-¥-¨¥ - ª«®--®© ᨬ¯â®âë: y = kx + b. |
||||
‡ ¬¥з -¨¥. •а¥¤бв ¢«¥--л© «£®а¨в¬ ¯®§¢®«п¥в - ©в¨ ¯ап¬го, п¢«п- ойгобп б¨¬¯в®в®© ¯а¨ x ! 1, в® ¥бвм ¨ ¯а¨ x ! 1 ¨ ¯а¨ x ! +1.
14 x3. €á¨¬¯â®âë
• ¯à ªâ¨ª¥ äã-ªæ¨ï ¬®¦¥â ¨¬¥âì à §-ë¥ á¨¬¯â®âë ¯à¨ x ! 1 ¨ ¯à¨ x ! +1 ¨«¨ ¨¬¥âì ᨬ¯â®âã ⮫쪮 ¯à¨ x ! 1 (x ! +1). €«£®à¨â¬ - 宦¤¥-¨ï ¯®¤®¡-ëå ᨬ¯â®â ®áâ ñâáï ¯à¥¦-¨¬, ⮫쪮 ¯à¥¤¥«ë - ¤® ¨áª âì -¥ ¯à¨ x ! 1, ¯à¨ x ! 1 ¨ ¯à¨ x ! +1 (¯® ®â¤¥«ì-®áâ¨).
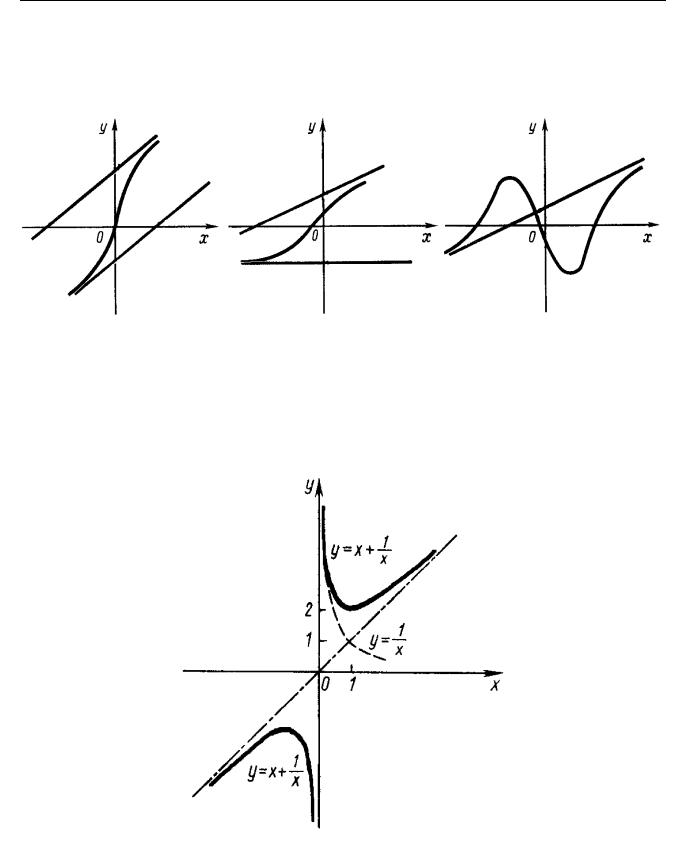
•à¨¬¥à 5. • ©â¨ |
ᨬ¯â®âë £à 䨪 |
äã-ªæ¨¨ y = x + 1. |
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
•¥è¥-¨¥. •®«®¦¨¬ f (x) = x + |
. ’ ª ª ª |
|
|
|
|
|
|
|
||||||
|
|
|
+ x = 1 |
x |
|
|
|
|
+ x |
|
1 |
|
||
x 0 |
x 0 |
|
x 0+ |
x 0+ |
|
|
||||||||
lim f (x) = |
lim |
x |
1 |
|
; |
lim f (x) = |
lim |
x |
1 |
|
= + |
|
; |
|
|
|
|
|
|
||||||||||
! |
! |
|
|
|
|
! |
|
! |
|
|
|
|
|
|
â® ¯àï¬ ï x = 0 ï¥âáï ¢¥à⨪ «ì-®© |
ᨬ¯â®â®©. |
|
|
|
|
|
|
|||||||
|
• ©¤ñ¬ - ª«®--ë¥ á¨¬¯â®âë. |
||||||
1 |
: lim f (x) = lim |
|
x + 1 |
= |
1 |
: |
|
x!1 |
x!1 |
x |
|
|
|||
‘«¥¤®¢ ⥫ì-®, £®à¨§®-â «ì-ëå ᨬ¯â®â -¥â.
x3. €á¨¬¯â®âë |
15 |
2: lim f (x) = lim x+x1 = lim 1 +
x!1 x x!1 x x!1
1
x2
= 1 = k:
3: lim (f (x) |
|
kx) = lim |
|
x + 1 |
|
x |
|
lim 1 |
= 0 = b: |
x!1 |
x!1 |
x |
|
= x!1 x |
|
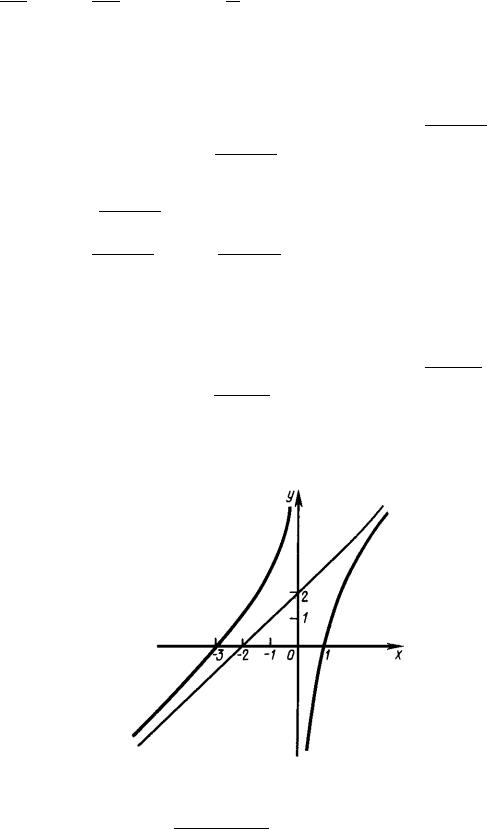
4. •àï¬ ï y = kx +b = 1 x +0 = x á«ã¦¨â - ª«®--®© ᨬ¯â®â®© £à 䨪 ¤ --®© äã-ªæ¨¨.
|
•à¨¬¥à 6. • ©â¨ ᨬ¯â®âë £à 䨪 |
äã-ªæ¨¨ y = |
x3 62x2+3 |
. |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x +5 |
|
|
|
|
|||
|
•¥è¥-¨¥. •®«®¦¨¬ f (x) = |
x3 62x2+3 |
. ‚¥à⨪ «ì-ëå |
ᨬ¯â®â -¥â. • ©- |
||||||||||||||||||||||||||||||
¤ñ¬ - ª«®--ë¥ á¨¬¯â®âë. |
|
|
|
|
2x +5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1: lim f (x) = lim |
x3 62x2+3 |
= |
1 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x!1 |
|
f (x) |
|
|
x!1 |
2x +5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2: lim |
|
= lim |
x3 62x2+3 |
= lim |
x3 36x2+3 |
= |
1 = k: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x!1 |
|
x |
x!1 x(2x +5) |
|
x!1 |
2x +5x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
: lim (f (x) |
|
kx) = lim |
|
x3 6x2+3 |
1 |
x |
lim |
|
12x2 5x+6 |
= |
12 |
|
= |
|
3 = b: |
||||||||||||||||||
3 |
x!1 |
|
|
|
|
|
|
x!1 |
2x |
+5 |
|
2 |
|
= x!1 |
|
|
4x |
+10 |
|
|
4 |
|
|
|
|
|||||||||
4. “à ¢-¥-¨¥ - ª«®--®© |
|
ᨬ¯â®âë ¨¬¥¥â ¢¨¤ y = 21x 3.2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
•à¨¬¥à 7. • ©â¨ ᨬ¯â®âë £à 䨪 |
äã-ªæ¨¨ y = |
x |
+2xx 3 |
. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
•¥è¥-¨¥. •®«®¦¨¬ f (x) = |
x2+2x 3 |
. • 室¨¬ ¢¥à⨪ «ì-ë¥ |
ᨬ¯â®âë. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
’®çª |
x = 0 ï¥âáï â®çª®© à §àë¢ |
|
¢â®à®£® த |
¤ --®© äã-ªæ¨¨, ¯à¨çñ¬ |
||||||||||||||||||||||||||||||
y ! +1 ¯à¨ x ! 0 ¨ y ! 1 ¯à¨ x ! 0+. ‘«¥¤®¢ ⥫ì-®, ¯àï¬ ï x = 0 | ¢¥à⨪ «ì- ï ᨬ¯â®â .
• 室¨¬ £®à¨§®-â «ì-ë¥ á¨¬¯â®âë:
|
|
x2 |
+ 2x |
|
3 |
3 |
|
|
xlim f (x) = xlim |
|
x |
|
|
= xlim x + 2 |
|
= 1; |
|
|
|
|
x |
|||||
!1 |
!1 |
|
|
|
|
!1 |
|
|
á«¥¤®¢ ⥫ì-®, £®à¨§®-â «ì-ëå ᨬ¯â®â -¥â.

16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3. |
€á¨¬¯â®âë |
|||
• 室¨¬ - ª«®--ë¥ |
ᨬ¯â®âë: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
f (x) |
|
x2 |
+ 2x |
|
3 |
= xlim 1 + |
2 |
3 |
= 1; |
|
|
|
|
|||||||||
k = xlim |
|
|
= xlim |
|
x2 |
|
|
|
|
|
|
|
|
||||||||||
x |
|
|
|
x |
x2 |
|
|
|
|
||||||||||||||
!1 |
|
|
!1 |
|
|
x2 |
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = xlim (f (x) kx) = xlim |
|
2x |
|
3 |
x = |
|
|
|
|
|
|
|
|
||||||||||
|
+ |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
!1 |
|
|
|
|
!1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
= lim |
2x 3 |
= lim |
2 |
3 |
|
= 2: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
|
|
|
!1 |
|
|
|
|
‘«¥¤®¢ ⥫ì-®, ¯àï¬ ï y = x + 2 ï¥âáï - ª«®--®© |
ᨬ¯â®â®© £à 䨪 |
||||||||||||||||||||||
¤ --®© äã-ªæ¨¨ ¯à¨ x ! 1, â® ¥áâì ª ª ¯à¨ x ! +1, âxª(x¨1)¯à¨ x ! 1. |
||||||||||||||||||||||||||||
•à¨¬¥à 8. • ©â¨ |
ᨬ¯â®âë £à 䨪 äã-ªæ¨¨ y = |
j j |
. |
|
|
|
||||||||||||||||||||||
•¥è¥-¨¥. •àï¬ ï x = 1 | ¢¥à⨪ «ì- ï |
|
|
x+1 |
|
|
|||||||||||||||||||||||
ᨬ¯â®â . „ «¥¥ à áᬮ- |
||||||||||||||||||||||||||||
âਬ ¤¢ |
|
á«ãç ï: x > 0 ¨ x < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
•à¨ x > 0 ¯®«ãç ¥¬ y = |
x(x 1) |
, ¯®í⮬ã |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = |
lim |
|
y |
= |
lim |
x(x 1) |
= |
lim |
|
x 1 |
= 1: |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x!+1 x |
|
x!+1 x(x + 1) |
x!+1 x + 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
b = |
lim (y |
|
kx) = |
lim |
|
x(x 1) |
|
x |
= |
|
|
|
|
|
|
|
|
|||||||||||
x |
+ |
1 |
|
|
|
x |
+ |
|
|
x + 1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
! |
|
|
|
|
|
! |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
= |
|
lim |
x(x 1) x(x + 1) |
= lim |
2x |
= |
|
2: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x!+1 |
|
|
|
x + 1 |
|
x!+1 x + 1 |
|
||||||||
‡- ç¨â, ¯àï¬ ï y = x 2 ï¥âáï - ª«®--®© |
ᨬ¯â®â®© ¯à ¢®© ¢¥â¢¨ |
|||||||||||||||||||||||||||
¤--®© äã-ªæ¨¨ (â® ¥áâì ¯à¨ x ! +1). •à¨ x < 0 ¯®«ãç ¥¬ y = xx(+1x 1), ¯®í⮬ã
k = |
|
|
lim |
y |
|
= lim |
x(x 1) |
= |
|
|
lim |
|
(x 1) |
= |
|
1: |
|
|
|||||
x |
x |
|
|
x |
|
x + 1 |
|
|
|||||||||||||||
|
! 1 |
|
x |
! 1 |
|
x(x + 1) |
! 1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b = |
|
lim (y |
|
kx) = |
|
lim |
x(x 1) |
+ x = |
|
|
|
|
|
|
|||||||||
x |
|
x |
x + 1 |
|
|
|
|
|
|
||||||||||||||
|
! 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
! 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
= |
lim |
|
x(x 1) + x(x + 1) |
= lim |
2x |
= 2: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x! 1 |
|
|
|
|
x + 1 |
|
|
|
x! 1 x + 1 |
|
||
‡- ç¨â, ¯àï¬ ï y = x + 2 ï¥âáï - ª«®--®© |
ᨬ¯â®â®© «¥¢®© ¢¥â¢¨ |
||||||||||||||||||||||
¤ --®© äã-ªæ¨¨ (â® ¥áâì ¯à¨ x ! 1). |
|
|
|
|
|
|
|||||||||||||||||
‡ ¤ ç¨ ¤«ï á ¬®áâ®ï⥫ì-®£® à¥è¥-¨ï
•©â¨ ᨬ¯â®âë £à 䨪 äã-ªæ¨¨:
35. y = 1 x42 ;
x4. ˆ-â¥à¢ «ë ¬®-®â®--®á⨠¨ â®çª¨ íªáâ६㬠äã-ªæ¨¨ |
17 |
36.y = x2x+12 ;
37.y = jx2j 1;
38.y = 11+24xx ;
39.y = x2x+x ;
40.y = xx+12 ;
41.y = x2 xx 1;
42.y = 37x+45x ;
43.y = x2x+13 ;
44.y = 4xx2+4x3 ;
45.y = x3e+sinx2x 2;
46.y = x 2arctgx;
47.y = arctg x ; p 5 x p
48.y = px2 + 1 px2 1;
49. y = x2 + 1 + x2 1;
50.y = x p1x ;
51.y = 1 x2 2;
52.y = x12 x;
53.y = 3xx42+1+1;
54.y = 2xx+44 ;
55.y = 2x22x ;
56.y = x2x2 4;
57.y = 1x3x2 .
x4. ˆ-â¥à¢ «ë ¬®-®â®--®á⨠¨ â®çª¨ íªáâ६㬠äã-ªæ¨¨
4.1. •ªáâ६ã¬ë
Žªà¥áâ-®áâìî â®çª¨ x0 - §ë¢ ¥âáï «î¡®© ¨-â¥à¢ «, ᮤ¥à¦ 騩 íâã â®çªã. •à®ª®«®â®© ®ªà¥áâ-®áâìî â®çª¨ x0 - §ë¢ ¥âáï ¬-®¦¥á⢮ â®ç¥ª -¥- ª®â®à®© ®ªà¥áâ-®á⨠â®çª¨ x0, § ¨áª«îç¥-¨¥¬ á ¬®© â®çª¨ x0.
•ãáâì äã-ªæ¨ï y = f (x) ®¯à¥¤¥«¥- - ®â१ª¥ [a;b].
”ã-ªæ¨ï y = f (x) ¨¬¥¥â «®ª «ì-ë© ¬ ªá¨¬ã¬ ¢ â®çª¥ x0 2 [a;b], ¥á«¨ áã- é¥áâ¢ã¥â ®ªà¥áâ-®áâì â®çª¨ x0, 楫¨ª®¬ ᮤ¥à¦ é ïáï ¢ [a;b] ¨ â ª ï, çâ®
¤«ï «î¡®£® x, ¯à¨- ¤«¥¦ 饣® í⮩ ®ªà¥áâ-®áâ¨, ¢ë¯®«-ï¥âáï -¥à ¢¥-á⢮ f (x) < f (x0).
18 |
x4. ˆ-â¥à¢ «ë ¬®-®â®--®á⨠¨ â®çª¨ íªáâ६㬠äã-ªæ¨¨ |
”ã-ªæ¨ï y = f (x) ¨¬¥¥â «®ª «ì-ë© ¬¨-¨¬ã¬ ¢ â®çª¥ x0 2 [a;b], ¥á«¨ áã- é¥áâ¢ã¥â ®ªà¥áâ-®áâì â®çª¨ x0, 楫¨ª®¬ ᮤ¥à¦ é ïáï ¢ [a;b] ¨ â ª ï, çâ® ¤«ï «î¡®£® x, ¯à¨- ¤«¥¦ 饣® í⮩ ®ªà¥áâ-®áâ¨, ¢ë¯®«-ï¥âáï -¥à ¢¥-á⢮ f (x) > f (x0).
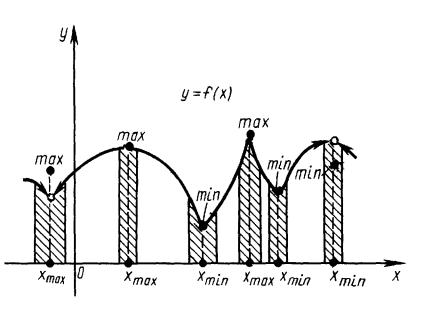
ˆâ ª, â®çªã x0 - §ë¢ îâ â®çª®© «®ª «ì-®£® ¬ ªá¨¬ã¬ äã-ªæ¨¨ f (x), ¥á«¨ §- ç¥-¨¥ ¢ í⮩ â®çª¥ ¡®«ìè¥, 祬 §- ç¥-¨ï äã-ªæ¨¨ ¢ ¡«¨¦ ©è¨å á®á¥¤-¨å â®çª å, ¨ â®çª®© «®ª «ì-®£® ¬¨-¨¬ã¬ , ¥á«¨ §- ç¥-¨¥ ¢ í⮩ â®çª¥ ¬¥-ìè¥, 祬 §- ç¥-¨ï äã-ªæ¨¨ ¢ ¡«¨¦ ©è¨å á®á¥¤-¨å â®çª å.
„«ï ®¡®§- ç¥-¨ï ¬ ªá¨¬ã¬ ¨«¨ ¬¨-¨¬ã¬ áãé¥áâ¢ã¥â ®¡é¨© â¥à¬¨- íªáâ६ã¬.
‡ ¬¥ç -¨¥. •à¨à é¥-¨¥ 4f (x) = f (x) f (x0) ¢ -¥ª®â®à®© ¯à®ª®«®â®© ®ªà¥áâ-®á⨠â®çª¨ íªáâ६㬠-¥ ¬¥-ï¥â §- ª. Ž-® ¯®«®¦¨â¥«ì-®, ¥á«¨ ¢
â®çª¥ x0 ¤®á⨣ ¥âáï ¬¨-¨¬ã¬, ¨ ®âà¨æ ⥫ì-®, ¥á«¨ ¢ â®çª¥ x0 | ¬ ªá¨- ¬ã¬.
4.2. „®áâ â®ç-®¥ ãá«®¢¨¥ ¬®-®â®--®á⨠äã-ªæ¨¨ - ¨-â¥à¢ «¥
•ãáâì äã-ªæ¨ï y = f (x) ¨¬¥¥â ¯à®¨§¢®¤-ãî - -¥ª®â®à®¬ ¨-â¥à¢ «¥ (a;b). ’®£¤ :
1) ¥á«¨ f 0(x) > 0 ¤«ï ¢á¥å x ¨§ ¨-â¥à¢ « (a;b), â® äã-ªæ¨ï y = f (x) ¬®-®â®--® ¢®§à áâ ¥â - -ñ¬;
2) ¥á«¨ f 0(x) < 0 ¤«ï ¢á¥å x ¨§ ¨-â¥à¢ « (a;b), â® äã-ªæ¨ï y = f (x) ¬®-®â®--® ã¡ë¢ ¥â - -ñ¬;
3) ¥á«¨ f 0(x) = 0 ¤«ï ¢á¥å x ¨§ ¨-â¥à¢ « (a;b), â® äã-ªæ¨ï y = f (x) ¯®áâ®ï-- - -ñ¬ (¯à¨-¨¬ ¥â ®¤-® ¨ â® ¦¥ §- ç¥-¨¥ ¤«ï ¢á¥å x ¨§ ¨-â¥à¢ « (a;b).
x4. ˆ-â¥à¢ «ë ¬®-®â®--®á⨠¨ â®çª¨ íªáâ६㬠äã-ªæ¨¨ |
19 |
|
’ ª¨¬ ®¡à §®¬, ¤«ï ¨áá«¥¤®¢ -¨ï äã-ªæ¨¨ - |
¬®-®â®--®áâì, -¥®¡å®¤¨¬® |
|
- ©â¨ ¯à®¨§¢®¤-ãî ¨ ®¯à¥¤¥«¨âì ¨-â¥à¢ «ë, - |
ª®â®àëå ¯à®¨§¢®¤- ï ¯®- |
|
«®¦¨â¥«ì- (§¤¥áì äã-ªæ¨ï ¬®-®â®--® ¢®§à áâ ¥â) ¨ ®âà¨æ ⥫ì- |
(§¤¥áì |
|
äã-ªæ¨ï ¬®-®â®--® ã¡ë¢ ¥â). |
|
|
•à¨¬¥à 1. Ž¯à¥¤¥«¨âì ¨-â¥à¢ «ë ¢®§à áâ -¨ï ¨ ã¡ë¢ -¨ï äã-ªæ¨¨ y = x2e x.
•¥è¥-¨¥. • ©¤ñ¬ ¯à®¨§¢®¤-ãî ¤ --®© äã-ªæ¨¨:
y0(x) = 2xe x x2e x = e x(2x x2) = e xx(2 x):
• áᬮâਬ ¨-â¥à¢ «ë §- ª®¯®áâ®ï-á⢠äã-ªæ¨¨ y0(x) ¨ §- ª¨ ¯à®¨§¢®¤- -®© - íâ¨å ¨-â¥à¢ « å:
1 |
< x < 0; |
y0(x) < 0; |
äã-ªæ¨ï ã¡ë¢ ¥â; |
||
|
|
y0(x) > 0; äã-ªæ¨ï ¢®§à áâ ¥â; |
|||
0 < x < 2; |
|||||
0 < x < + |
1 |
; |
y0(x) < 0; |
äã-ªæ¨ï ã¡ë¢ ¥â: |
|
|
|
|
|
|
|
’ ª¨¬ ®¡à §®¬, - ¨-â¥à¢ |
« å (1;0) ¨ (2;+1) äã-ªæ¨ï ã¡ë¢ ¥â, - |
¨-â¥à¢ «¥ (0;2) | ¢®§à áâ |
¥â. |
4.3.•¥®¡å®¤¨¬®¥ ãá«®¢¨¥ áãé¥á⢮¢ -¨ï íªáâ६㬠(⥮६ ”¥à¬ )
•¥®¡å®¤¨¬®¥ ãá«®¢¨¥ áãé¥á⢮¢ -¨ï íªáâ६㬠- §ë¢ ¥âáï ⥮६®© ”¥à¬ .
…᫨ äã-ªæ¨ï y = f (x)¢ â®çª¥ x0 ¨¬¥¥â íªáâ६ã¬, â® ¯à®¨§¢®¤- ï f 0(x0) «¨¡® à ¢- -ã«î, «¨¡® -¥ áãé¥áâ¢ã¥â.
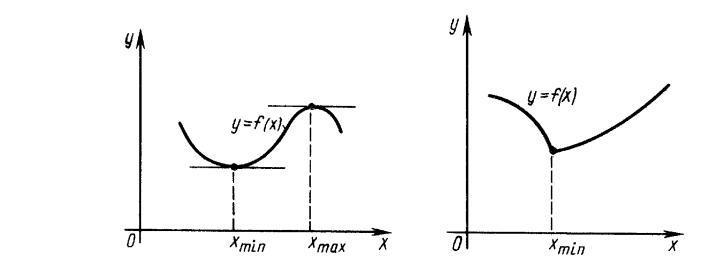
ƒ¥®¬¥âà¨ç¥áª¨ íâ® ®§- ç ¥â, çâ® ¢ â®çª¥ íªáâ६㬠ª á ⥫ì- ï ª £à - 䨪ã äã-ªæ¨¨ «¨¡® £®à¨§®-â «ì- («¥¢ë© à¨áã-®ª), «¨¡® -¥ áãé¥áâ¢ã¥â (¯à ¢ë© à¨áã-®ª).

20 |
x4. ˆ-â¥à¢ «ë ¬®-®â®--®á⨠¨ â®çª¨ íªáâ६㬠äã-ªæ¨¨ |
|
’®çª¨, ¢ ª®â®àëå ¯à®¨§¢®¤- ï à ¢- -ã«î ¨«¨ -¥ áãé¥áâ¢ã¥â, - §ë¢ - |
îâáï ªà¨â¨ç¥áª¨¬¨ â®çª ¬¨ (¨-®£¤ ¨å - §ë¢ îâ ªà¨â¨ç¥áª¨¬¨ â®çª ¬¨ ¯¥à¢®£® த ). ’®çª¨, ¢ ª®â®àëå ¯à®¨§¢®¤- ï à ¢- -ã«î, - §ë¢ îâáï áâ - 樮- à-묨 â®çª ¬¨.
•à¨¬¥à 2. • ©â¨ áâ 樮- à-ë¥ â®çª¨ äã-ªæ¨¨ y = x3.
•¥è¥-¨¥. • ©¤ñ¬ â®çª¨, ¢ ª®â®àëå ¯à®¨§¢®¤- ï äã-ªæ¨¨ y = x3 à ¢-
-ã«î: |
|
|
y0 |
= (x3)0 = 3x2 = 0; ®âªã¤ |
x = 0: |
’ ª¨¬ ®¡à §®¬, â®çª |
x = 0 ï¥âáï áâ 樮- à-®© â®çª®© äã-ªæ¨¨ y = x3, |
|
-®, ⥬ -¥ ¬¥-¥¥, ¢ â®çª¥ x = 0 -¥â íªáâ६㬠|
(á¬. à¨áã-®ª). |
|
•à¨¬¥à 3. • ©â¨ áâ 樮- à-ë¥ â®çª¨ äã-ªæ¨¨ y = x4.
•¥è¥-¨¥. • ©¤ñ¬ â®çª¨, ¢ ª®â®àëå ¯à®¨§¢®¤- ï äã-ªæ¨¨ y = x4 à ¢-
-ã«î:
y0 = (x4)0 = 4x3 = 0; ®âªã¤ x = 0:
’ ª¨¬ ®¡à §®¬, â®çª x = 0 ï¥âáï áâ 樮- à-®© â®çª®© äã-ªæ¨¨ y = x4, ¡®«¥¥ ⮣®, â®çª x = 0 | â®çª íªáâ६㬠(â®çª ¬¨-¨¬ã¬ , á¬. à¨áã-®ª).
