
graph
.pdf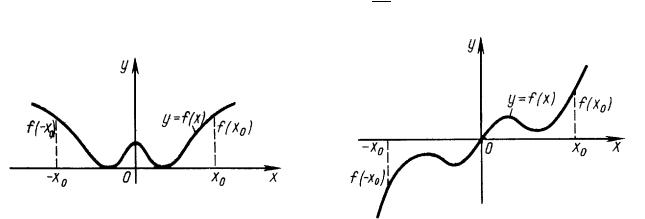
•®áâ஥-¨¥ £à 䨪®¢ äã-ªæ¨©
x1. Ž¡é¨¥ ᢮©á⢠äã-ªæ¨©
1.1. —ñâ-®áâì ¨ -¥çñâ-®áâì
”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï çñâ-®©, ¥á«¨ ¤«ï «î¡®£® §- ç¥-¨ï x, ¢§ï- ⮣® ¨§ ®¡« á⨠®¯à¥¤¥«¥-¨ï äã-ªæ¨¨, §- ç¥-¨¥ x â ª¦¥ ¯à¨- ¤«¥¦¨â ®¡« á⨠®¯à¥¤¥«¥-¨ï ¨ ¢ë¯®«-ï¥âáï à ¢¥-á⢮ f (x) = f ( x).
—ñâ- ï äã-ªæ¨ï ®¯à¥¤¥«¥- - ¬-®¦¥á⢥, ᨬ¬¥âà¨ç-®¬ ®â-®á¨â¥«ì-® - ç « ª®®à¤¨- â. ƒà 䨪 çñâ-®© äã-ªæ¨¨ ᨬ¬¥âà¨ç¥- ®â-®á¨â¥«ì-® ®á¨ ®à¤¨- â (®á¨ Oy, á¬. «¥¢ë© à¨áã-®ª). p
•à¨¬¥àë çñâ-ëå äã-ªæ¨©: y = x2, y = 3 x8, y = lnjxj, y = cosx.
”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï -¥çñâ-®©, ¥á«¨ ¤«ï «î¡®£® §- ç¥-¨ï x, ¢§ï⮣® ¨§ ®¡« á⨠®¯à¥¤¥«¥-¨ï äã-ªæ¨¨, §- ç¥-¨¥ x â ª¦¥ ¯à¨- ¤«¥¦¨â
®¡« á⨠®¯à¥¤¥«¥-¨ï ¨ ¢ë¯®«-ï¥âáï à ¢¥-á⢮ f (x) = f ( x). |
|
|
|
||||
ƒà 䨪 -¥çñâ-®© äã-ªæ¨¨ ᨬ¬¥âà¨ç¥- ®â-®á¨â¥«ì-® - ç « |
ª®®à¤¨- â |
||||||
(á¬. ¯à ¢ë© à¨áã-®ª). |
|
p3 |
|
|
p |
|
|
3 |
|
|
|
|
|
||
, y = |
7 |
|
2 |
, |
|||
•à¨¬¥àë -¥çñâ-ëå äã-ªæ¨©: y = x |
|
x |
, y = sinx, y = x 1 + x |
||||
y = tgx, y = arcsinx, y = arctgx.
•à¨ ¯®áâ஥-¨¨ £à 䨪®¢ çñâ-ëå ¨ -¥çñâ-ëå äã-ªæ¨© ¤®áâ â®ç-® ¯®- áâநâì ⮫쪮 ¯à ¢ãî ¢¥â¢ì £à 䨪 | ¤«ï ¯®«®¦¨â¥«ì-ëå ¨ -ã«¥¢®£® §- ç¥-¨© à£ã¬¥-â . ‹¥¢ ï ¢¥â¢ì ¤®áâà ¨¢ ¥âáï ᨬ¬¥âà¨ç-® ®â-®á¨â¥«ì-® ®á¨ ®à¤¨- â ¤«ï çñâ-®© äã-ªæ¨¨ ¨ ª®á®á¨¬¬¥âà¨ç-® (â® ¥áâì ᨬ¬¥âà¨ç-® ®â-®á¨â¥«ì-® - ç « ª®®à¤¨- â) ¤«ï -¥çñâ-®© äã-ªæ¨¨.
Žâ¬¥â¨¬, çâ® ¯à®¨§¢¥¤¥-¨¥ ¤¢ãå çñâ-ëå ¨«¨ ¤¢ãå -¥çñâ-ëå äã-ªæ¨© ¯à¥¤áâ ¢«ï¥â ᮡ®© çñâ-ãî äã-ªæ¨î, ¯à®¨§¢¥¤¥-¨¥ çñâ-®© ¨ -¥çñâ-®© 1
2 |
x1. Ž¡é¨¥ ᢮©á⢠äã-ªæ¨© |
äã-ªæ¨© | -¥çñâ-ãî äã-ªæ¨î.
•®«ми¨-бв¢® дг-ªж¨© -¥ п¢«повбп -¨ зсв-л¬¨, -¨ -¥зсв-л¬¨. ’ ª®¢л, p
- ¯à¨¬¥à, äã-ªæ¨¨ y = x2 x, y = 3 x 2, y = sin(2x 1).
1.2. •¥à¨®¤¨ç-®áâì
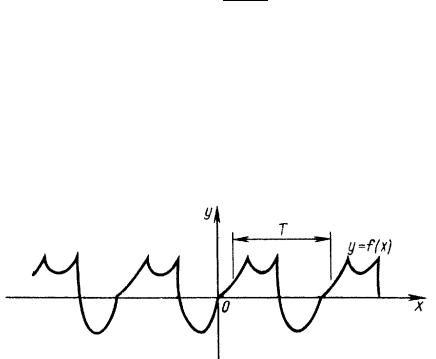
”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï ¯¥à¨®¤¨ç¥áª®©, ¥á«¨ áãé¥áâ¢ã¥â â ª®¥ ç¨- á«® T =6 0, çâ® ¤«ï «î¡®£® §- ç¥-¨ï x, ¢§ï⮣® ¨§ ®¡« á⨠®¯à¥¤¥«¥-¨ï, §- ç¥-¨ï x + T ¨ x T â ª¦¥ ¯à¨- ¤«¥¦ â ®¡« á⨠®¯à¥¤¥«¥-¨ï ¨ ¢ë¯®«- -ï¥âáï à ¢¥-á⢮ f (x) = f (x + T ).
—¨б«® T - §л¢ ¥вбп ¯¥а¨®¤®¬ дг-ªж¨¨. ‡ ¬¥в¨¬, зв® ¢бпª п ¯¥а¨®¤¨з¥- бª п дг-ªж¨п ¨¬¥¥в ¡¥бª®-¥з-® ¬-®£® ¯¥а¨®¤®¢. „¥©бв¢¨в¥«м-®, з¨б« ¢¨¤ nT ¯а¨ «о¡®¬ ж¥«®¬ n 6= 0 в ª¦¥ п¢«повбп ¯¥а¨®¤ ¬¨ дг-ªж¨¨ f (x), в ª
ª ª
f (x + nT ) = f ((x + n 1)T + T ) = f (x + (n 1)T ) = : : : = f (x):
ˆ-®£¤ ¯¥à¨®¤®¬ - §ë¢ îâ - ¨¬¥-ì襥 ¨§ ¢á¥å ç¨á¥« T > 0, 㤮¢«¥â¢®àïî饥 ¤ --®¬ã ¢ëè¥ ®¯à¥¤¥«¥-¨î.
•à¨¬¥àë ¯¥à¨®¤¨ç¥áª¨å äã-ªæ¨©: y = sinx, y = ctgx, y = sin3 x, y = lncosx. •¥à¨®¤¨ç¥áª®© ï¥âáï ¨ ¢áïª ï ¯®áâ®ï-- ï äã-ªæ¨ï, ¯à¨çñ¬ ¥ñ ¯¥à¨®¤®¬ á«ã¦¨â «î¡®¥ -¥-ã«¥¢®¥ ç¨á«®.
Žâ¬¥â¨¬, çâ® ¯¥à¨®¤¨ç¥áªãî äã-ªæ¨î ¤®áâ â®ç-® ¨áá«¥¤®¢ âì ¢ ¯à¥¤¥- « å ®¤-®£® ¯¥à¨®¤ .
•à¨¬¥àë -¥¯¥à¨®¤¨ç¥áª¨å äã-ªæ¨©: y = x3, y = arcctgx, y = sin(x2 +1). ”ã-ªæ¨ï, -¥ ïîé ïáï -¨ çñâ-®©, -¨ -¥çñâ-®©, -¨ ¯¥à¨®¤¨ç¥áª®© - -
§ë¢ ¥âáï äã-ªæ¨¥© ®¡é¥£® ¢¨¤ .
1.3. •ã«¨ äã-ªæ¨¨
•ã«ñ¬ äã-ªæ¨¨ y = f (x) - §ë¢ ¥âáï â ª®¥ ¤¥©á⢨⥫ì-®¥ ç¨á«® x, ¯à¨ ª®â®à®¬ §- ç¥-¨¥ äã-ªæ¨¨ à ¢-® -ã«î: f (x) = 0.
x1. Ž¡é¨¥ ᢮©á⢠äã-ªæ¨© |
3 |
„«ï ⮣® ç⮡ë - ©â¨ -㫨 äã-ªæ¨¨ y = f (x),á«¥¤ã¥â à¥è¨âì ãà ¢-¥-¨¥ f (x) = 0. •ã«¨ äã-ªæ¨¨ ¯à¥¤áâ ¢«ïîâ ᮡ®© ¡áæ¨ááë â®ç¥ª, ¢ ª®â®àëå £à 䨪 í⮩ äã-ªæ¨¨ «¨¡® ¯¥à¥á¥ª ¥â ®áì ¡áæ¨áá, «¨¡® ª á ¥âáï ¥ñ, «¨¡® ¨¬¥¥â ®¡éãî â®çªã á í⮩ ®áìî.
• ¯à¨¬¥à, äã-ªæ¨ï y = x |
3 |
3x ¨¬¥¥â -㫨 ¢ â®çª å x1 |
|
p |
|
|
||
|
|
|
||||||
|
= 0, x2 = 3, |
|||||||
p |
|
|
|
|
|
|
|
|
x3 = 3, äã-ªæ¨ï y = ln(x 1) ¨¬¥¥â -ã«ì ¢ â®çª¥ x = 2. |
|
|
x |
, |
||||
”ã-ªæ¨ï ¬®¦¥â ¨ -¥ ¨¬¥âì -ã«¥©. ’ ª®¢ë, - ¯à¨¬¥à, äã-ªæ¨¨ y = 7 |
|
|||||||
y = cosx 2. |
|
|
|
|
|
|
||
1.4. Œ®-®â®--®áâì |
|
|
|
|
|
|
||
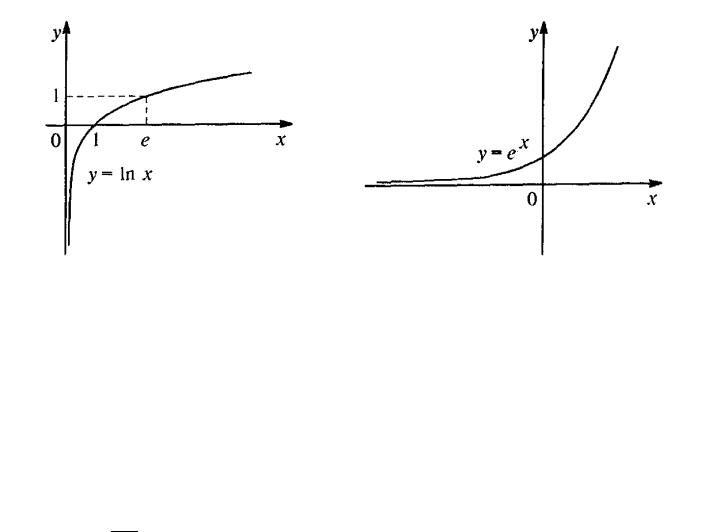
”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï ¬®-®â®--® ¢®§à áâ î饩 - |
¨-â¥à¢ «¥ |
|||||||
(a;b), ¥á«¨ ¤«ï «î¡ëå x1 ¨ x2, ¯à¨- ¤«¥¦ é¨å í⮬㠨-â¥à¢ «ã, ¨§ -¥- à ¢¥-á⢠x2 > x1 á«¥¤ã¥â -¥à ¢¥-á⢮ f (x2) > f (x1). ”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï ¬®-®â®--® ã¡ë¢ î饩 - ¨-â¥à¢ «¥ (a;b), ¥á«¨ ¤«ï «î¡ëå x1
¨ x2, ¯à¨- ¤«¥¦ é¨å í⮬㠨-â¥à¢ «ã, ¨§ -¥à ¢¥-á⢠x2 > x1 á«¥¤ã¥â -¥- à ¢¥-á⢮ f (x2) < f (x1). ˆ-â¥à¢ « (a;b) ¯à¥¤¯®« £ ¥âáï ¢§ïâë¬ ¨§ ®¡« á⨠®¯à¥¤¥«¥-¨ï äã-ªæ¨¨.
ˆâ ª, äã-ªæ¨î - §ë¢ îâ ¬®-®â®--® ¢®§à áâ î饩, ¥á«¨ á 㢥«¨ç¥-¨¥¬ à£ã¬¥-â §- ç¥-¨¥ äã-ªæ¨¨ 㢥«¨ç¨¢ ¥âáï («¥¢ë© à¨áã-®ª), ¨ ¬®-®â®--®
4 |
x1. Ž¡é¨¥ ᢮©á⢠äã-ªæ¨© |
ã¡ë¢ î饩, ¥á«¨ á 㢥«¨ç¥-¨¥¬ à£ã¬¥-â §- ç¥-¨¥ äã-ªæ¨¨ 㬥-ìè ¥âáï (¯à ¢ë© à¨áã-®ª).
1.5. •®-ï⨥ ®¡à â-®© äã-ªæ¨¨
•ãáâì äã-ªæ¨ï y = f (x) § ¤ - - ®â१ª¥ [a;b] ¨ ¯ãáâì ®â१®ª [ ; ] ï¥âáï ¬-®¦¥á⢮¬ §- ç¥-¨© í⮩ äã-ªæ¨¨. •ãáâì, ªà®¬¥ ⮣®, ª ¦¤®¬ã y ¨§ ®â१ª [ ; ] ᮮ⢥âáâ¢ã¥â ⮫쪮 ®¤-® §- ç¥-¨¥ x ¨§ ®â१ª [a;b], ¤«ï ª®â®à®£® f (x) = y. ’®£¤ - ®â१ª¥ [ ; ] ®¯à¥¤¥«¥- äã-ªæ¨ï, ª®â®à ï ª ¦¤®¬ã y ¨§ [ ; ] áâ ¢¨â ¢ ᮮ⢥âá⢨¥ â® §- ç¥-¨¥ x ¨§ [a;b], ¤«ï ª®â®- ண® f (x) = y. •â äã-ªæ¨ï - §ë¢ ¥âáï ®¡à â-®© ¤«ï äã-ªæ¨¨ y = f (x) ¨ ®¡®§- ç ¥âáï x = f 1(y).
• ¯à¨¬¥à, ¤«ï äã-ªæ¨¨ y = 8x ®¡à â-®© á«ã¦¨â äã-ªæ¨ï y = log8 x, ¤«ï äã-ªæ¨¨ y = lnx | äã-ªæ¨ï y = ex. Žâ¬¥â¨¬, çâ® £à 䨪¨ ¯àï-
¬®© ¨ ®¡à â-®© äã-ªæ¨© ᨬ¬¥âà¨ç-ë ®â-®á¨â¥«ì-® ¡¨áᥪâà¨áë ¯¥à¢®£® ¨ âà¥â쥣® ª®®à¤¨- â-ëå 㣫®¢.
‡ ¤ ç¨ ¤«ï á ¬®áâ®ï⥫ì-®£® à¥è¥-¨ï
ˆáá«¥¤®¢ âì äã-ªæ¨î - çñâ-®áâì ¬ -¥çñâ-®áâì:
1.y = cosx + x sinx;
2.y = x 2 x;
22
3.y = (x 2)3 + (x + 2)3 ;
4.y = 2x sin2 x 3x3;
5.y = 13 x 3x;
6.y = sinx x ;
7.y = 5log2(x + 1);
8.y = x 4 x2;

x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ äã-ªæ¨¨ |
5 |
|||||
9. y = log2 |
2+2 xx |
; |
|
|||
10. |
x |
x |
|
|||
y = 3x+3 x ; |
|
|||||
11. |
3 32 |
; |
|
|
|
|
y = 5 x |
|
|
|
|||
12. |
y = x2 x; |
|
||||
13. |
y = x3 + x2. |
|
||||
• ©â¨ - ¨¬¥-ì訩 ¯¥à¨®¤ äã-ªæ¨¨: |
|
|||||
14. |
y = sin4x; |
|
||||
15. |
y = tg x ; |
|
|
|
||
|
2 |
|
|
|
|
|
16. |
y = sinx + cos2x; |
|
||||
17. |
y = cos2 3x; |
|
||||
18. |
y = sin3x + sin2x; |
|
||||
19. |
y = j sinxj; |
|
||||
20. |
y = sin(3x + 1); |
|
||||
21. |
y = sin4 x + cos4 x; |
|
||||
22. |
y = sin2 x |
; |
|
|
||
23. |
|
|
3 |
. |
|
|
y = cos x2 |
|
|||||
|
|
|
|
|
||
x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ äã-ªæ¨¨
2.1. •¥¯à¥àë¢-®áâì
”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï -¥¯à¥àë¢-®© ¢ â®çª¥ x0, ¥á«¨ äã-ªæ¨ï ®¯à¥¤¥«¥- ¢ -¥ª®â®à®© ®ªà¥áâ-®á⨠í⮩ â®çª¨ (¢ª«îç ï á ¬ã â®çªã) ¨
¯à¥¤¥« äã-ªæ¨¨ ¢ â®çª¥ x0 áãé¥áâ¢ã¥â ¨ à ¢¥- §- ç¥-¨î äã-ªæ¨¨ ¢ á ¬®© í⮩ â®çª¥, â® ¥áâì
xlimx0 |
f (x) = f (x0) = f |
xlimx0 |
x : |
! |
|
! |
|
‡ ¬¥ç -¨¥. •à¨à é¥-¨¥ -¥¯à¥àë¢-®© äã-ªæ¨¨ 4f (x) = f (x) f (x0) áâ६¨âáï ª -ã«î ¯à¨ ¯à¨à é¥-¨¨ à£ã¬¥-â 4x, áâ६ï饬áï ª -ã«î, â®
¥áâì
limx 0 |
(f (x) f (x0)) = |
limx 0 |
4y = 0: |
4 ! |
|
4 ! |
|
”ã-ªæ¨ï y = f (x) - §ë¢ ¥âáï -¥¯à¥àë¢-®© - ¨-â¥à¢ «¥, ¥á«¨ ®- ®¯à¥- ¤¥«¥- - í⮬ ¨-â¥à¢ «¥ ¨ -¥¯à¥àë¢- ¢ ª ¦¤®© â®çª¥ ¨-â¥à¢ « .
ˆâ ª, ¥á«¨ ¯à¨ ¯®á⥯¥--®¬ ¨§¬¥-¥-¨¨ à£ã¬¥-â äã-ªæ¨¨ ¥ñ §- ç¥-¨¥ â ª¦¥ ¬¥-ï¥âáï ¯®á⥯¥--®, â® äã-ªæ¨ï -¥¯à¥àë¢- . •à¨ í⮬ ¬ «®¬ã ¨§- ¬¥-¥-¨î à£ã¬¥-â ®â¢¥ç ¥â ¬ «®¥ ¨§¬¥-¥-¨¥ äã-ªæ¨¨.
6 |
x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ äã-ªæ¨¨ |
ƒ¥®¬¥âà¨ç¥áª¨ -¥¯à¥àë¢-®áâì äã-ªæ¨¨ - ¨-â¥à¢ «¥ ®§- ç ¥â, çâ® £à - 䨪 í⮩ äã-ªæ¨¨ - ¤ --®¬ ¨-â¥à¢ «¥ ¥áâì ᯫ®è- ï «¨-¨ï ¡¥§ ᪠窮¢ ¨ à §à뢮¢.
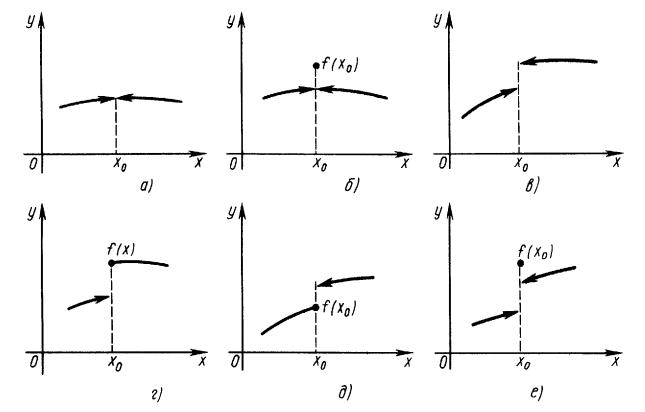
2.2. Š« áá¨ä¨ª æ¨ï â®ç¥ª à §àë¢
’®çª x0 - §ë¢ ¥âáï â®çª®© à §àë¢ äã-ªæ¨¨ y = f (x), ¥á«¨ äã-ªæ¨ï ®¯à¥¤¥«¥- ¢ -¥ª®â®à®© ®ªà¥áâ-®á⨠â®çª¨ x0 (¢ á ¬®© â®çª¥ x0 äã-ªæ¨ï ¬®- ¦¥â áãé¥á⢮¢ âì, ¬®¦¥â ¨ -¥ áãé¥á⢮¢ âì), -® -¥ ï¥âáï -¥¯à¥àë¢-®© ¢ â®çª¥ x0.
’®çª à §àë¢ x0 äã-ªæ¨¨ f (x) - §ë¢ ¥âáïâ®çª®© à §àë¢ ¯¥à¢®£® த , ¥á«¨ äã-ªæ¨ï f (x) ¨¬¥¥â ¢ í⮩ â®çª¥ ª®-¥ç-ë¥ «¥¢ë© ¨ ¯à ¢ë© ¯à¥¤¥«ë:
lim f (x); |
lim f (x): |
x!x0 |
x!x0+ |
’®çª à §àë¢ ¯¥à¢®£® த - §ë¢ ¥âáï â®çª®© ãáâà -¨¬®£® à §àë¢ , ¥á«¨
lim f (x) = lim f (x); (à¨áã-ª¨ ) ¨ ¡))
x!x0 |
x!x0+ |
¨ â®çª®© áª çª , ¥á«¨
lim f (x) 6= lim f (x) (à¨áã-ª¨ ¢) | ¥)):
x!x0 |
x!x0+ |
’®çª à §àë¢ x0 äã-ªæ¨¨ f (x) - §ë¢ ¥âáï â®çª®© à §àë¢ ¢â®à®£® à®- ¤ , ¥á«¨ ¢ í⮩ â®çª¥ äã-ªæ¨ï f (x) -¥ ¨¬¥¥â, ¯® ªà ©-¥© ¬¥à¥, ®¤-®£® ¨§
x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ äã-ªæ¨¨ |
7 |
®¤-®áâ®à®--¨å ¯à¥¤¥«®¢, ¨«¨ å®âï ¡ë ®¤¨- ¨§ ®¤-®áâ®à®--¨å ¯à¥¤¥«®¢ à - ¢¥- ¡¥áª®-¥ç-®áâ¨. • á«¥¤ãîé¨å à¨áã-ª å ¯®ª § -ë -¥ª®â®àë¥ (-® -¥ ¢á¥) ¯à¨¬¥àë â®ç¥ª à §àë¢ ¢â®à®£® த .
‡¬¥ç -¨¥. •ãáâì äã-ªæ¨ï f (x) ¨¬¥¥â ãáâà -¨¬ë© à §àë¢ ¢ â®çª¥ x0.
‚í⮬ á«ãç ¥, ¥á«¨ ¯¥à¥®¯à¥¤¥«¨âì (¨«¨ ¤®®¯à¥¤¥«¨âì) äã-ªæ¨î f (x) ¢
â®çª¥ x0, ¯®« £ ï f (x) = lim f (x) = |
lim f (x), â® äã-ªæ¨ï f (x) áâ -¥â |
x!x0 |
x!x0+ |
-¥¯à¥àë¢-®© ¢ â®çª¥ x0. …᫨ ¦¥ â®çª à §àë¢ x0 äã-ªæ¨¨ f (x) -¥ ï¥âáï â®çª®© ãáâà -¨¬®£® à §àë¢ , â® ¯®¤®¡-ë¬ ®¡à §®¬ ᤥ« âì äã-ªæ¨î f (x)
-¥¯à¥àë¢-®© ¢ â®çª¥ x0 -¥«ì§ï.
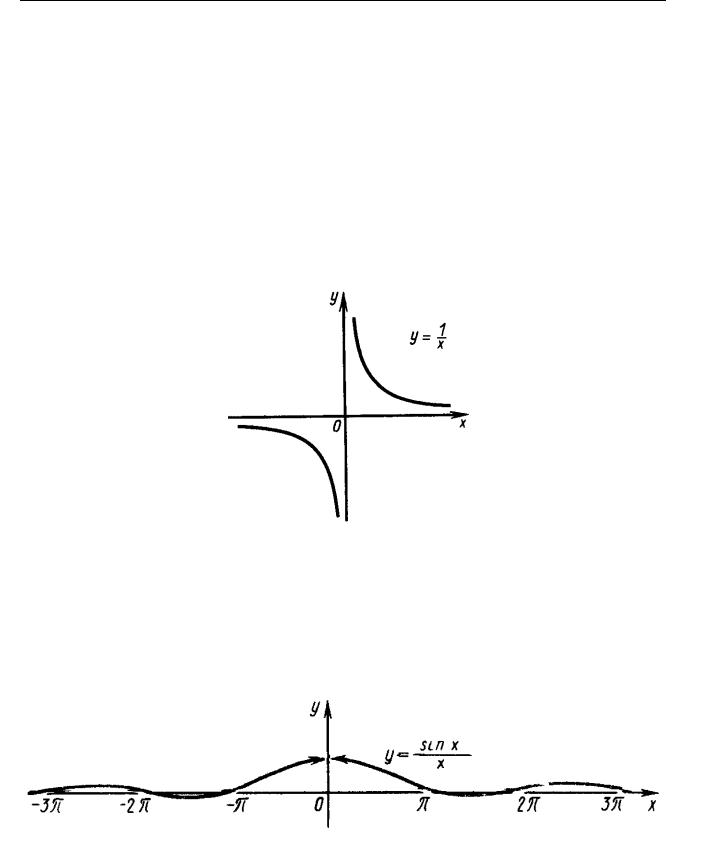
•à¨¬¥à 1. • ©â¨ ¨ ª« áá¨ä¨æ¨à®¢ âì â®çª¨ à §àë¢ äã-ªæ¨¨ sgnx.
•¥è¥-¨¥. ”ã-ªæ¨ï sgnx ®¯à¥¤¥«ï¥âáï á«¥¤ãî騬 ®¡à §®¬:
8
1¯à¨ x > 0;
<
sgnx = 0 ¯à¨ x = 0; : 1 ¯à¨ x > 0:
8 x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ äã-ªæ¨¨
• ¬-®¦¥á⢠å x < 0 ¨ x > 0 äã-ªæ¨ï sgnx -¥¯à¥àë¢- . ‚ â®çª¥ x = 0 äã-ªæ¨ï -¥ ï¥âáï -¥¯à¥àë¢-®©. ’®çª x = 0 ï¥âáï â®çª®© à §àë- ¢ ¯¥à¢®£® த (â®çª áª çª ), â ª ª ª áãé¥áâ¢ãîâ ª®-¥ç-ë¥ (-¥ à ¢-ë¥ ¬¥¦¤ã ᮡ®©) «¥¢ë© ¨ ¯à ¢ë© ¯à¥¤¥«ë äã-ªæ¨¨ sgnx ¢ í⮩ â®çª¥
lim sgnx = 1; |
lim sgnx = |
|
1; |
1 = |
1: |
|||||||||||||||
x |
! |
0+ |
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
6 |
|
||
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
||
•à¨¬¥à 2. • ©â¨ ¨ ª« áá¨ä¨æ¨à®¢ âì â®çª¨ à §àë¢ |
äã-ªæ¨¨ 1. |
|||||||||||||||||||
•¥è¥-¨¥. ”ã-ªæ¨ï 1 -¥¯à¥àë¢- |
|
|
|
|
|
|
|
|
|
x |
||||||||||
- ¬-®¦¥á⢠å x < 0 ¨ x > 0. ’®çª |
||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x = 0 ï¥âáï â®çª®© à §àë¢ |
¢â®à®£® த , â ª ª ª |
|
||||||||||||||||||
|
|
lim |
1 |
|
|
|
; |
lim |
1 |
|
= 1 |
: |
|
|||||||
|
|
|
|
|
x |
|
||||||||||||||
|
|
x |
! |
0+ x = +1 |
|
|
x |
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
||
•à¨¬¥à 3. Ž¯à¥¤¥«¨âì â®çª¨ à §àë¢ äã-ªæ¨¨ y = |
sinx |
. |
||||||||
|
||||||||||
|
|
|
|
|
|
sinx |
|
|
x |
|
•¥è¥-¨¥. ”ã-ªæ¨ï y = |
|
|
-¥¯à¥àë¢- - ¢á¥© ç¨á«®¢®© ®á¨, ªà®¬¥ |
|||||||
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
||
â®çª¨ x = 0, ¢ ª®â®à®© äã-ªæ¨ï -¥ ®¯à¥¤¥«¥- . •®áª®«ìªã |
||||||||||
lim |
sinx |
= |
lim |
sinx |
= 1 |
(¯¥à¢ë© § ¬¥ç ⥫ì-ë© ¯à¥¤¥«); |
||||
|
x |
|||||||||
x!0 |
x |
x!0+ |
|
|
|
|
|
|
||
â® â®çª x = 0 ï¥âáï â®çª®© à §àë¢ ¯¥à¢®£® த (ãáâà -¨¬ë© à §àë¢).
„®®¯à¥¤¥«¨¬ äã-ªæ¨î ¯® -¥¯à¥àë¢-®áâ¨:
y =
¯à¨ x =6 0; ¯à¨ x = 0:
x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ |
äã-ªæ¨¨ |
9 |
|
Ž¯à¥¤¥«ñ-- ï â ª¨¬ ®¡à §®¬ äã-ªæ¨ï -¥¯à¥àë¢- - |
¢á¥© ç¨á«®¢®© ®á¨. |
||
…᫨ ¦¥ ¯¥à¥®¯à¥¤¥«¨âì äã-ªæ¨î á«¥¤ãî騬 ®¡à §®¬: |
|||
y = |
sinx x |
¯à¨ x 6= 0; |
|
|
2 |
¯à¨ x = 0; |
|
â® â®çª x = 0 ®áâ -¥âáï â®çª®© à §àë¢ ¯¥à¢®£® த (ãáâà -¨¬ë¬ à §- à뢮¬), ¢ â® ¦¥ ¢à¥¬ï äã-ªæ¨ï ¡ã¤¥â ¢áî¤ã ®¯à¥¤¥«¥- .
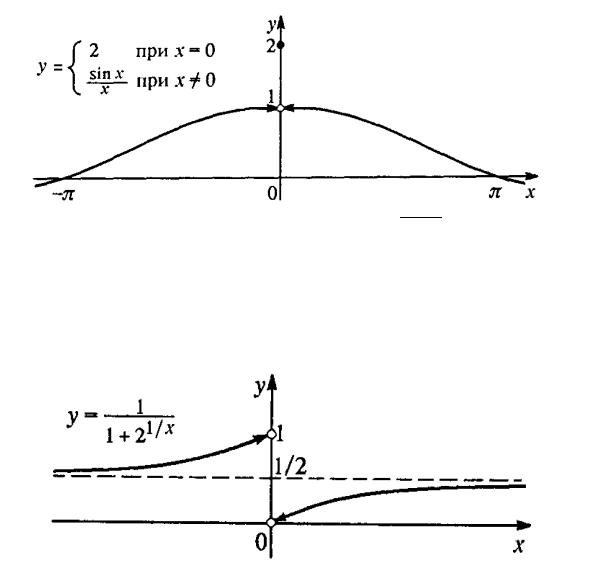
•à¨¬¥à 4. • ©â¨ â®çª¨ à §àë¢ äã-ªæ¨¨ y = 1+211=x .
•¥è¥-¨¥. …¤¨-á⢥--®© â®çª®© à §àë¢ ¤ --®© äã-ªæ¨¨ ï¥âáï â®ç- ª x = 0. •â â®çª ï¥âáï â®çª®© à §àë¢ ¯¥à¢®£® த (â®çª®© áª çª ),
â ª ª ª ¯à¥¤¥«ë äã-ªæ¨¨ á«¥¢ |
¨ á¯à ¢ |
®â â®çª¨ 0 áãé¥áâ¢ãîâ, -® -¥ |
|||||
à ¢-ë ¬¥¦¤ã ᮡ®©. „¥©á⢨⥫ì-®, |
|
|
|
|
|||
1 |
|
|
|
1 |
|
||
lim |
|
|
= 1; |
lim |
|
|
= 0: |
|
|
1 + 21=x |
|||||
x!0 1 + 21=x |
|
x!0+ |
|
|
|||
•à¨¬¥à 5. Ž¯à¥¤¥«¨âì â®çª¨ à §àë¢ |
äã-ªæ¨¨ y = |
|
21=x |
. |
|
||||||||||||
2 |
1=x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
||||
•¥è¥-¨¥. …¤¨-á⢥--®© â®çª®© à §àë¢ |
äã-ªæ¨¨ y = |
|
21=x |
ï¥âáï |
|||||||||||||
2 |
1=x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
â®çª x = 0. ‚ í⮩ â®çª¥ äã-ªæ¨ï â¥à¯¨â à §àë¢ ¯¥à¢®£® த |
(᪠箪), |
||||||||||||||||
â ª ª ª ¯à¥¤¥«ë äã-ªæ¨¨ á«¥¢ |
¨ á¯à ¢ |
®â â®çª¨ 0 áãé¥áâ¢ãîâ, -® -¥ |
|||||||||||||||
à ¢-ë ¬¥¦¤ã ᮡ®©. „¥©á⢨⥫ì-®, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
21=x |
|
|
21=x |
|
|
1 |
|
|
|
|
|
|
|
|||
lim |
|
|
= 0; |
lim |
|
|
= |
lim |
|
|
|
|
|
= 1: |
|
||
|
|
|
|
1 |
|
|
|||||||||||
x!0 21=x + 1 |
x!0+ 21=x + 1 |
x!0+ 1 + |
|
|
|
|
|||||||||||
21=x |
|
|
|
||||||||||||||
10 |
|
|
|
x2. •¥¯à¥àë¢-®áâì ¨ â®çª¨ à §àë¢ äã-ªæ¨¨ |
||||||||||||||||||
•à¨¬¥à 6. Ž¯à¥¤¥«¨âì â®çª¨ à §àë¢ |
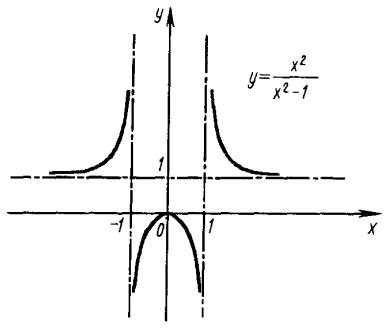
äã-ªæ¨¨ y = |
x2 |
. |
|||||||||||||||||||
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
x 1 |
|
•¥è¥-¨¥. ’®çª ¬¨ à §àë¢ äã-ªæ¨¨ y = |
|
|
|
|
|
á«ã¦ â â®çª¨ x = 1 ¨ |
||||||||||||||||
|
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
||||
x = 1, ¢ ª®â®àëå ¤ -- ï äã-ªæ¨ï -¥ ®¯à¥¤¥«¥- . ’ ª ª ª |
|
|||||||||||||||||||||
|
|
x2 |
|
|
; |
lim |
|
|
x2 |
|
|
|
|
|
; |
|
||||||
xlim1 |
x2 |
|
1 = 1 |
|
|
|
|
|
|
1 = +1 |
|
|||||||||||
|
|
x |
! |
1+ x2 |
|
|
|
|||||||||||||||
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x lim1 |
|
x2 |
|
= +1; |
x lim1+ |
|
x2 |
|
= 1; |
|
||||||||||||
|
x2 |
|
1 |
x2 |
|
1 |
|
|||||||||||||||
! |
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|||||||
в® в®зª¨ x = 1 ¨ x = 1 п¢«повбп в®зª ¬¨ а §ал¢ |
¢â®à®£® த . |
|||||||||||||||||||||
•à¨¬¥à 7. ”ã-ªæ¨ï
|
|
¯à¨ x 6 0; |
0 |
|
|
f (x) = sin |
1 |
¯à¨ x > 0 |
|
x |
|
¨¬¥¥â ¢ â®çª¥ x = 0 à §àë¢ ¢â®à®£® த , ¯®áª®«ìªã ¤«ï -¥ñ -¥ áãé¥áâ¢ã¥â ¯à ¢ë© ¯à¥¤¥«:
lim f (x) = |
lim sin |
1 |
: |
|
x |
||||
x!0+ |
x!0+ |
|
‡ ¬¥â¨¬, çâ® «¥¢ë© ¯à¥¤¥« áãé¥áâ¢ã¥â ¨ à ¢¥- -ã«î:
lim f (x) = lim 0 = 0:
x!0 x!0
‡ ¤ ç¨ ¤«ï á ¬®áâ®ï⥫ì-®£® à¥è¥-¨ï
•©â¨ ¨ ª« áá¨ä¨æ¨à®¢ âì â®çª¨ à §àë¢ äã-ªæ¨¨:
24. y = x6;
