
Sintez_rychazhnykh_mekhanizmov
.pdf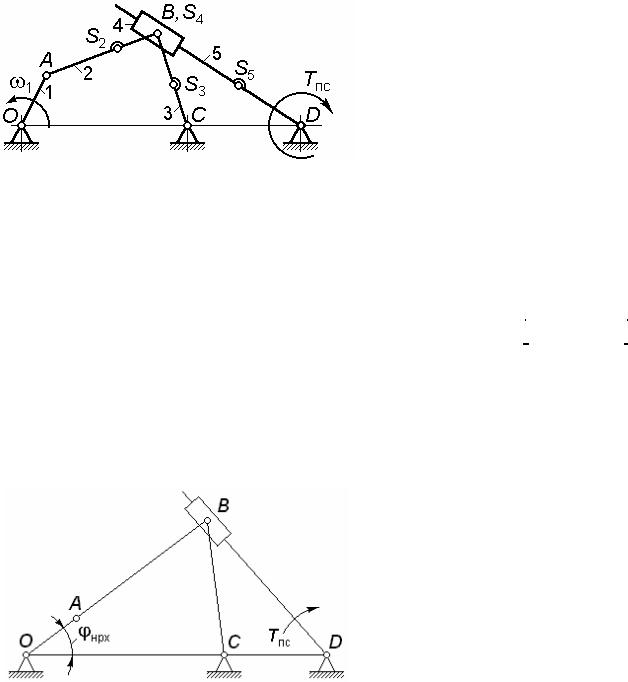
Кинематическая схема 27 |
|
|
|
|
Заданы: |
|
|
|
длина кривошипа OA; |
||
|
соотношение |
размеров |
|
|
OC и OA |
|
|
|
OC = α OA |
(27.1) |
|
Рис. 27.1 |
(параметр |
α задан как |
|
диапазон); |
|
|
|
соотношение размеров CD и OC |
|
|
|
|
|
|
|
CD =β OC ; |
|
|
(27.2) |
(параметр β задан как диапазон);
условие подбора длин звеньев AB и BC − угол ABC = γ при работе механизма должен изменяться в заданных пределах 
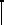
 γmin... γmax
γmin... γmax  , при этом должно соблюдаться соотношение AB ≥ BC .
, при этом должно соблюдаться соотношение AB ≥ BC .
Решение
Вначале выбираем размер OC из диапазона, определяемого соотношением (27.1) и затем − CD из (27.2).
|
|
Для выбора подходящих |
|
|
значений AB и BC воспользу- |
||
|
емся |
следующим |
способом: |
|
из ∆ ABC на схеме механиз- |
||
|
ма |
видим, |
что |
|
угол |
ABC = γ |
принимает |
|
предельное значение γmax , |
||
|
когда AC = ACmax =OC +OA |
||
Рис. 27.2 |
ответственно γmin , когда |
||
AC = ACmin =OC −OA; |
тогда очевидно, что для подбора длин AB и |
||
BC, удовлетворяющих условиям синтеза, можно использовать уравнения:
AB |
2 |
+ BC |
2 |
2 |
|
|
|
|
−2 AB BC cos γmax = ACmax ; |
(27.3) |
|||
|
2 |
|
2 |
2 |
|
|
AB |
+ BC |
|
|
|||
|
|
−2 AB BC cos γmin = ACmin ; |
|
|||
60
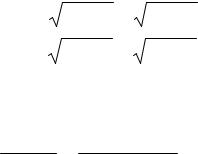
их решение найдем в виде: введем обозначения |
|
|||||||||||
P = |
AC2 |
|
cos γ |
min |
− AC2 |
cos γ |
max |
; |
(27.4) |
|||
|
max |
|
|
|
min |
|
||||||
|
|
cos γmin −cos γmax |
|
|||||||||
|
|
|
|
|
|
|
||||||
Q = |
|
AC2 |
|
− AC |
2 |
; |
|
|
|
(27.5) |
||
|
|
max |
|
min |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
cos γmin −cos γmax |
|
|
|
|
||||||
тогда длины звеньев |
|
|
|
|
|
|
|
|||||
BC = 0.5( |
P +Q − |
|
|
|
|
|
|
|||||
P −Q); |
|
|
( 27.6) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
AB = 0.5( |
P +Q + |
|
|
|
|
|
|
|||||
P −Q). |
|
|
|
|||||||||
Очевидно, что искомое решение существует только при P ≥Q , или, как это можно показать, при
λ = ACmax ≤ sin((0.5γmax )). ( 27.7 )
ACmin sin 0.5γmin
Несоблюдение неравенства (27.7) означает, что исходные данные выбраны не совсем удачно и требуют корректировки, которая может быть произведена разными способами:
можно расширить пределы допустимых углов [γmin ...γmax ] за счет
только нижней границы, выбрав ее из неравенства |
|
γmin ≤ 2 arcsin((sin(0.5γmax ))/ λ), |
( 27.8) |
или за счет только верхней границы - |
|
γmax ≥ 2 arcsin(λsin(0.5γmin )); |
( 27.9) |
можно также сохранить неизменным среднее значение |
|
γm = (γmin + γmax ) / 2 , |
(27.10) |
и назначить новые верхнюю и нижнюю границы: |
(27.11) |
γmax = γm ± ∆ |
|
min |
|
где вспомогательный угол ∆ может быть любым, удовлетворяющим неравенству
λ-1 |
|
γ |
m |
|
|
||
∆ ≥ ∆min = 2 arctg |
|
|
tg |
|
. |
(27.12) |
|
λ+1 |
|
|
|||||
|
|
2 |
|
||||
Рис. 27.2
После назначения новых пределов γmax и γmin можно воспользоваться формулами (27.4) − (27.6).
61
Найдем угол ϕнрх , определяющий положение кривошипа OA в момент начала рабочего хода механизма и кулисы 5
ϕнрх = arccos |
(AB +OA)2 +OC2 − BC2 . |
(27.13) |
|
2(AB +OA)BC |
|
Угол ϕкрх , определяющий положение кривошипа в момент
окончания рабочего хода кулисы 5 найдем из аналогичной расчетной схемы по формуле
ϕкрх =180o +arccos |
(AB −OA)2 +OC2 − BC2 . |
(27.13) |
|
2(AB −OA)OC |
|
Для определения величины рабочего хода кулисы ψ существуют аналитические формулы, но ввиду их громоздкости более оправданным считаем обращение для этой цели к компьютерной среде САМАС.
62
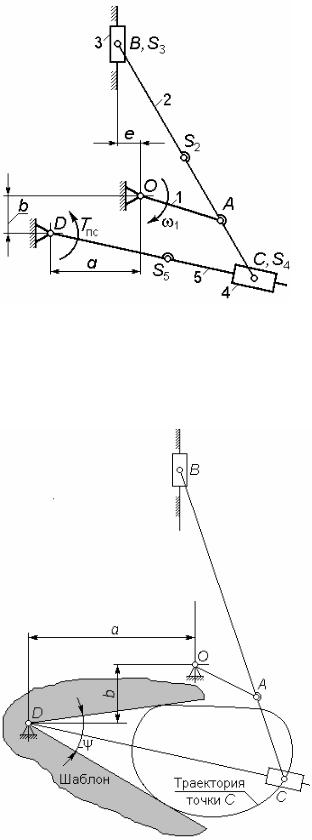
Кинематическая схема 28
Заданы:
длинакривошипаOA; координата добавочной точки на
шатуне−размерAC; эксцентриситет направляющей
ползуна3 – e;
соотношениеразмеровAB иOA
AB = α OA |
(28.1) |
(параметрα заданкакдиапазон); соотношениеразмеровb иAC
b = AC +0.1м; |
(28.2) |
требуемый угол |
качания ку- |
лисы 5 − ψ.
Рисунок 28.1 Необходимо подобрать размер шатуна AB и ординату а центра шар-
нира D, обеспечивая получение угла ψ с точностью ±2°.
|
Решение |
|
|
|
Размер AB находим из соот- |
||
|
ношения (28.1), а ординату b цен- |
||
|
тра шарнира D − по формуле |
||
|
(28.2). |
|
|
|
Для |
подбора |
подходящего |
|
значения размера a можно ис- |
||
|
пользовать |
компьютерную среду |
|
|
САМАС; при таком способе ре- |
||
|
шения абсциссе a задают ряд зна- |
||
|
чений, для каждого из них опре- |
||
|
деляют величину угла качания ψ |
||
|
и таким образом подбирают под- |
||
|
ходящую величину a; |
||
|
Можно также |
воспользо- |
|
|
ваться графическим методом: для |
||
|
этого из бумаги вырезают два уг- |
||
|
ловых шаблона с |
внутренними |
|
Рисунок 28.2 |
углами (ψ+2°) и (ψ-2°) и каждый |
||
63
из этих шаблонов поочередно пытаются поместить вершиной угла в такую точку D с ординатой b (рис. 28.2), чтобы траектория точки C (предварительно построенная) поместилась внутри указанного угла и касалась его сторон. Таким образом, будут найдены два предельных положения точки D и соответственно два предельных значения искомого расстояния − a max и amin ; в качестве окончательного значения
абсциссы a можно принять любое, удовлетворяющее неравенству и
a max ≥ a ≥ amin .
Угловые координаты кривошипа OA в моменты начала – ϕнрх и окончания – ϕкрх рабочего хода кулисы, а также фактическое значе-
ние ψ этого хода достаточно просто и точно можно определить в среде САМАС.
64
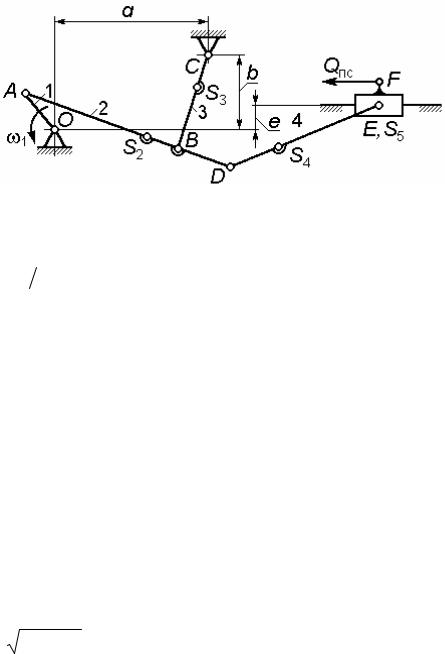
Кинематическая схема 29
Заданы: |
|
координаты a и b центра неподвижного шарнира C; |
|
соотношение размеров OC и OA |
|
OA = OC α; |
(29.1) |
соотношение размеров BD и AB |
|
BD = β AB |
(29.2) |
(коэффициент α и β заданы как диапазоны); эксцентриситет направляющей ползуна 5 − е;
условие подбора длин звеньев AB и BC − угол γ = ABC при работе механизма должен изменяться в заданных пределах [γmin ...γmax ], при этом должно соблюдаться соотношение AB ≤ BC;
длина шатуна DE должна быть подобрана так, чтобы угол его давления на ползун 5 (угол наклона шатуна к направляющей) не превышал заданной величины αmax .
Решение |
|
Определим размер OC |
|
OC = a2 +b2 |
(29.3) |
и по формуле (29.1) − длину кривошипа OA. |
|
Предельные значения расстояния AC |
|
ACmax =OC ±OA. |
(29.4) |
min |
|
Очевидно, что предельные значения размера |
AC и угла |
γ = ABC связаны уравнениями |
|
65
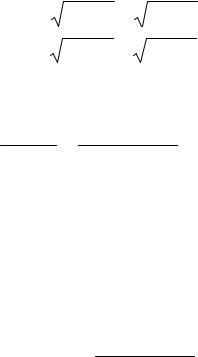
2 |
|
2 |
|
|
2 |
|
ACmax = AB |
|
+ BC |
|
−2 AB BC cos γmax ; |
||
2 |
2 |
|
2 |
|
||
|
|
|||||
ACmin = AB |
|
|
+ BC |
|
|
−2 AB BC cos γmin . |
Для их решения введем обозначения:
P = |
AC2 |
cos γ |
min |
− AC2 |
cos γ |
max |
; |
|||
|
max |
|
|
|
min |
|
||||
|
|
cos γmin −cos γmax |
|
|||||||
|
|
|
|
|
||||||
Q = |
|
AC2 |
|
− AC |
2 |
; |
|
|
|
|
|
max |
|
min |
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
cos γmin −cos γmax |
|
|
|
|||||
тогда длины звеньев
(29.5)
( 29.6)
( 29.7)
BC = 0.5( |
P +Q + |
|
|
P −Q); |
( 29.8) |
||
|
|
|
|
AB = 0.5( |
P +Q − |
|
|
P −Q). |
|
Очевидно, что искомое решение существует только при P ≥ Q, или, как это можно показать, при
λ = ACmax ≤ sin((0.5γmax )). ( 29.9)
ACmin sin 0.5γmin
Несоблюдение неравенства (29.9) означает, что исходные данные выбраны неудачно и требуют корректировки, которая может быть произведена тремя способами:
можно расширить пределы допустимых углов [γmin...γmax ] за счет
только нижней границы, выбрав ее из неравенства
γmin ≤ 2 arcsin sin(0.5γmax ) ,
λ
или за счет только верхней границы -
γmax ≥ 2 arcsin(λsin(0.5γmin ));
можно также сохранить неизменным среднее значение
γm = (γmin + γmax ) / 2 ,
иназначить новые верхнюю и нижнюю границы:
γmax = γm ± ∆,
min
( 29.9)
(29.10)
(29.11)
(29.12)
где вспомогательный угол ∆ может иметь любое значение, удовлетворяющее неравенству
66

λ-1 |
|
γ |
|
|
||
∆ ≥ ∆min = 2 arctg |
|
|
tg |
|
m . |
(29.13) |
λ+1 |
|
|||||
|
|
2 |
|
|||
Последний способ вынужденного расширения диапазона углов [γmin...γmax ] более предпочтителен.
Для подбора размера DE необходимо определить величину наибольшего по абсолютной величине удаления yDmax центра шарнира D
от горизонтальной направляющей ползуна 5 (это можно сделать, используя компьютерную среду САМАС, или графически - вычертив в подходящем масштабе траекторию точки D и замерив расстояние ее наиболее удаленной точки от направляющей). Тогда в качестве окончательного значения длины шатуна DE можно взять любое, удовлетворяющее неравенству
yD max |
|
DE ≥ sin α max . |
(29.18) |
Рабочий ход механизма начинается при положении кривошипа OA, определяемом углом ϕнрх (ползун 5 при этом занимает крайнее
левое положение) и заканчивается при ϕкрх − (ползун находится в
крайнем правом положении); значения этих углов и величину хода H5 рабочего звена можно найти только приближенно, но при исполь-
зовании компьютерной среды САМАС − с любой желаемой точностью.
67
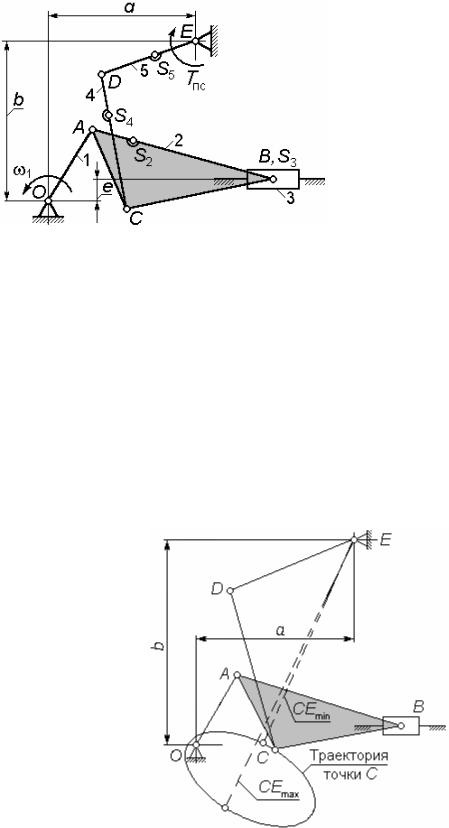
Кинематическая схема 30 |
|
|
|
|
Заданы: |
|
|
|
длина кривошипа OA; |
||
|
соотношение |
длин |
|
|
звеньев AB и OA |
|
|
|
AB = α OA |
(30.1) |
|
|
(параметр α задан как диа- |
||
|
пазон); |
|
|
|
параметры, определяю- |
||
|
щие положение добавочной |
||
Рисунок 30.1 |
точки C на шатуне - угол |
||
меров AC и OA |
BAC и соотношение раз- |
||
|
|
|
|
AC =β OA |
|
|
(30.2) |
(параметр β задан как диапазон); |
|
|
|
координаты a и b центра шарнира E; |
|
|
|
условие подбора длин звеньев CD и DE - |
угол γ = CDE при |
||
работе механизма должен |
изменяться в |
заданных |
пределах |
[γmin ...γmax ]. |
|
|
|
Решение
Размеры AB и AC находим из соотношений (30.1) и (30.2).
Рисунок 30.2
Для подбора приемлемых значений длин звеньев CD и DE необходимо вначале найти наибольшее CEmax и наименьшее CEmin значе-
68
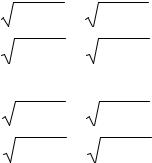
ния расстояния CE (рис. 30.2). Это можно сделать либо графически, измерив соответствующие отрезки на вычерченном в масштабе плане положений механизма, либо проведя необходимый анализ кинематической схемы в компьютерной среде САМАС.
Очевидно, что для подбора длин CD и DE, удовлетворяющих условиям синтеза, можно использовать уравнения, которые следуют из рассмотрения ∆CDE (рис. 30.2)
CD |
2 |
+ DE |
2 |
2 |
|
|
|
|
−2 CD DE cos γmax = CEmax ; |
( 30.3) |
|||
|
2 |
|
2 |
2 |
|
|
CD |
+ DE |
|
|
|||
|
|
−2 CD DE cos γmin = CEmin ; |
|
|||
для их решения найдем вспомогательные величины
|
CE 2 |
cos γ |
min |
−CE 2 |
cos γ |
max |
|
|
||
P = |
|
max |
|
|
min |
|
; |
( 30.4) |
||
|
|
cos γmin −cos γmax |
|
|||||||
|
|
|
|
|
|
|||||
Q = |
CEmax2 −CEmin2 |
; |
|
|
|
( 30.5) |
||||
cos γmin −cos γmax |
|
|
|
|||||||
тогда |
|
|
|
|
|
|
|
|
|
|
CD = 0.5( |
P +Q + |
|
|
|
|
|
|
|||
P −Q); |
|
|
( 30.6) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
DE = 0.5( |
P +Q − |
|
|
|
|
|
|
|||
P −Q), |
|
|
|
|||||||
или
CD = 0.5( |
P +Q − |
|
P −Q); |
||
|
|
|
DE = 0.5( |
P +Q + |
|
P −Q). |
Очевидно, что решения (30.6) и (30.7) существует только при
или, что то же самое, при |
||||
|
CEmax |
|
sin(0.5γmax ) |
|
λ = |
|
≤ |
|
. |
CEmin |
sin(0.5γmin ) |
|||
( 30.7)
P ≥Q ,
( 30.8)
Несоблюдение условия (30.8) означает, что исходные данные выбраны неудачно и требуют корректировки, которая может быть произведена тремя различными способами:
можно расширить пределы допустимых углов [γmin ...γmax ] за счет только нижней границы, выбрав ее из неравенства
1 |
γ |
max |
|
|
||
γmin ≤ 2 arcsin |
λ |
sin |
|
, |
( 30.9) |
|
|
|
|||||
|
|
2 |
|
|||
69
