МУ расчет контактора

6.4.3 Расчет обмотки переменного тока Так как тяговая характеристика электромагнита переменного

тока с внешним притягивающимся якорем является, как правило,

весьма пологой, то определение намагничивающей силы может быть произведено при минимальном значении рабочего зазора.

6.4.3.1 Определение намагничивающей силы С учетом падения магнитного потенциала и потерь в стали

получим

Fm (1,2 1,3)Bδδmin A.

μ0

6.4.3.2 Определение числа витков с учетом снижения напряжения на 15 %

W 0,85Uн витков.

4,44fBδSс

6.4.3.3 Определение действующего значения МДС

F Fm А. 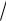2

6.4.3.4 Ток в обмотке

где λmin − проводимость при минимальном зазоре (δmin = 0,5мм),

λmin μδ0Sс Гн. min

6.4.3.5 Сечение провода

q aсWhсkз м2,

где kз − коэффициент заполнения, обычно принимается 0,4÷0,6.

44

6.4.3.7 Расчетный диаметр не изолированного провода

dпр 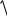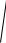4πq м.

Принимаем стандартный диаметр провода по табл. 11.

Таблица 11

Стандартные диаметры неизолированных проводов

dтаб

По стандартному диаметру dтаб рассчитывается qтаб и

уточняется число витков.

W aсhсkз витков.

qтаб

6.4.3.8 Сопротивление обмотки

R ρLсрW Ом,

qтаб

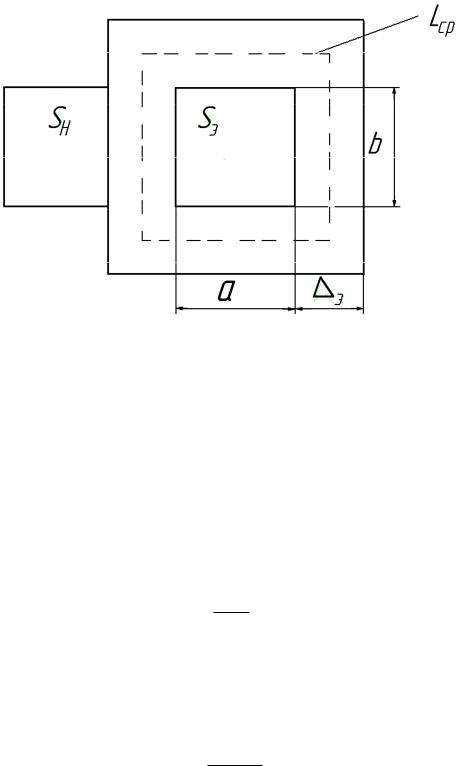
где Lср − длина средней линии

Lср 2(ас bс) 2π aкатм,

где aкат − радиальный размер катушки, м;

45

Wd2

aкат hтаб м.

с

6.4.3.9 Площадь поверхности охлаждения

Sохл 2Lср(aс hс) м2.

6.4.4 Расчет магнитной цепи с экраном

6.4.4.1 Расчет магнитного потока в рабочем зазоре (при притянутом якоре)

где Kнmin − коэффициент, учитывающий возможное понижение напряжения питания сети (Kнmin =0,6÷0,9); σсрпр − коэффициент рассеяния (σсрпр=1,03÷1,05).

6.4.4.2 Расчет коэффициента запаса

fэ 4α2 1,

где α − отношение площадей неэкранированной и экранированной частей, α=0,4÷0,6.

6.4.4.3 Расчет необходимого электрического сопротивления экрана

Rэ 4ωμδ0Sн+(3э ffээ 42)2f 2э Ом,

min

где Sн+э − сумма площадей неэкранированной и экранированной частей магнитопровода;

46

Sн+э acbc м.

6.4.4.4 Расчет угла между потоками Фн и Фэ при одновитковом экране

tgψ ωλэ,

Rэ

где λэ − магнитная проводимость экранированной части воздушного

зазора

λэ μδ0Sэ Гн,

min

где Sэ − площадь экранированной части, м;

Sэ Sн+э м.

1,5

6.4.4.5 Расчет магнитных потоков Поток в неэкранированной части

Фн сФδср Вб,

с cosψα .

Поток в экранированной части:

6.4.4.6 Расчет магнитной индукции в неэкранированной части зазора

Bн Фн Тл,

Sн

47

2) размеры определяют на основании теплового расчета экранированной области магнитопровода.

Выбор размеров экрана производят исходя из рис. 8.

Рис. 8. Эскиз электромагнитного экрана

Принимаем толщину экрана Э = 1,5-2 мм.

Длина средней линии экрана

Lсрэ 2(аэ bэ) 4 э) м,

где аЭ – ширина экрана аЭ=аС, м; bЭ – глубина экрана bЭ=0,6bC, м.

Электрическое сопротивление экрана

где qэ − сечение экрана, qэ aэbэ м2; ρ − удельное сопротивление медного экрана нагретого до температуры 200-250 °С.

Высота экрана

hLсрэρ0 м.

ээRэ

49

6.4.5 Расчет обмотки постоянного тока

6.4.5.1 Определение намагничивающей силы С учетом падения магнитного потенциала и потерь в стали

получим

Fm Bδδкр (1,2 1,6) A,

μ0

где δкр − критический зазор, м.

δкр 0,5 10 3 σп(1,5 2,5) м.

6.4.5.2 Определение действующего значения МДС

F 1,1 2,4Pвпн кр2 А.

μ0Sс

6.4.5.3 Сопротивление среднего витка с учетом понижения напряжения на 15 %

Rср20 1,34UнF Ом.

6.4.5.4 Сечение провода

q ρ20Lср м2,

Rср20

где ρ20 − удельное сопротивление при 20 °С; Lср − длина средней линии, м;

Lср π(dс dк) м,

где dк − диаметр катушки

dк dс (1 2) м.

6.4.5.5 Расчетный диаметр неизолированного провода

dпр 4πq м.

Принимаем стандартный диаметр провода по табл. 11.

50

По стандартному диаметру dтаб рассчитывается qтаб и

уточняется число витков.

W dсhсkз витков,

qтаб

где kз − коэффициент заполнения , обычно принимается 0,4÷0,6.

6.4.5.6 Сопротивление обмотки

R ρLсрW Ом.

qтаб

6.4.5.7 Площадь поверхности охлаждения

Sохл 2Lср(dс hс) м2.

6.4.5 Расчет проводимостей

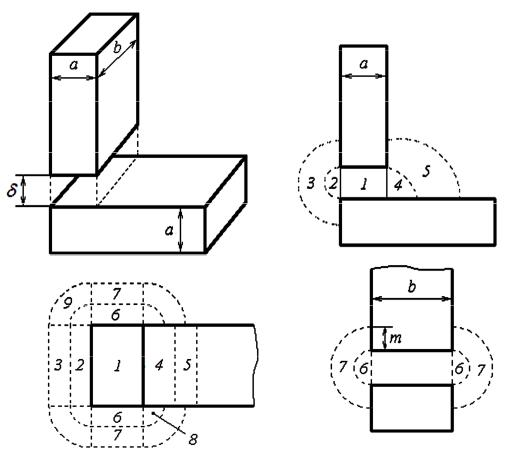
6.4.5.1 Схема замещения Проводимости рассчитываем методом разбивки поля на простые

геометрические фигуры (метод Роттерса или метод вероятных путей потока). Метод предусматривает разбиение объема пространства воздушного зазора на простые геометрические тела, ограниченные плоскостями, цилиндрическими, либо сферическими поверхностями.

Как правило, все частичные тела образуют вероятные параллельные пути общего магнитного потока в области воздушного зазора Фδ. Это обстоятельство определяет целесообразность расчета их параметров в форме частичных магнитных проводимостей Λδj, так что полная магнитная проводимость определяется суммированием частичных составляющих:

51

n

δ j 1 δj Гн.

В рассматриваемом методы частичная проводимость геометрического тела основной части воздушного зазора рассматривается как рабочая проводимость Λр =Λδ1, а остальные

n

фигуры создают краевую проводимость кр δj.

j 2

Поэтому соответственно для проводимости справедливо

Λδ= Λкр+ Λр Гн.

Рис.9. К расчету магнитной проводимости

воздушного зазора методом простых фигур

Выделяем простые фигуры согласно рис.9. При расчете

проводимости данным методом, важное значение имеет выбор

52

параметра m, учитывающего поток с боковых поверхностей полюса магнитной системы. Его значение определяется соотношением величины зазора δ к линейным размерам а и b, и принимают обычно m=(1-2)δ.

6.4.5.2 Расчет проводимостей производим для пяти зазоров:

1.Минимальный зазор δmin=0,5∙10-3 м.

2.Выбираем величину зазора значение, которого лежит между первым и третьим зазором.

3.Критический зазор δк = δmin+σп∙k м, (для переменного тока

k=(0,8-1,5), для постоянного тока k=(1,5-2,5)).

4.Выбираем величину зазора значение, которого лежит между третьим и пятым зазором.

5.Максимальный зазор δmax=δmin+β м.

Полная проводимость воздушного зазора представляет собой сумму всех частичных проводимостей, согласно рис. 9

λδi=λ1+λ2+λ3+λ4+λ5+2 λ6+2 λ7+4 λ8+4 λ9 Гн.

Фигура 1 − Призма высотой δ и основанием а и b

λ1 μ0δа b Гн.

Фигура 2 − Полуцилиндр диаметром δ длиной b

λ2 μ0 0,26 b Гн.

Фигура 3 − Половина полого цилиндра

53