Лабораторный практикум

Раздел VII. Методы управления инновационными проектами

n = 46; b = 26; w = b/n

и нажимаем клавишу Enter на клавиатуре.

После чего программа автоматически выведет на экран w – вероятность благоприятного исхода. Соответственно далее, можно определить вероятность неблагоприятного исхода событий – q, согласно (1). Для этого запишем следующую строку в командное окно MATLAB (рис. 4): q = 1- w, и нажимаем клавишу Enter на клавиатуре.

Рис. 4. Расчет риска инновационной деятельности

Таким образом, в результате были определены вероятности благоприятного w(b) и неблагоприятного исходов q(b) по количеству поставленных на серийное производство самолетов истребителей. Сравнить их численные значения и результаты занести в отчет.

2. Для выполнения второго задания лабораторного занятия – рассчитать величину дисперсии (2) и среднего квадратичного отклонения (3) по параметру тяги газотурбинных двигателей сверхзвуковых истребителей-перехватчиков по данным табл. 2 в системе

Microsoft Office Excel – запустим систему Microsoft Excel для ра-

боты с электронными таблицами, которая предоставляет возможности выполнения статистических расчетов. Для этого дважды «кликаем» левой кнопкой «мыши» по значку на рабочем столе

751

Раздел VII. Методы управления инновационными проектами

или в корневой директории (нажав левой клавишей «мыши» ме-

ню Пуск -> Microsoft Office -> Microsoft Excel 2007 или Microsoft Excel 2010) (также возможен вариант запуска системы с диска), после чего появится главное окно системы (рис. 5).

Рис. 5. Рабочее окно системы Microsoft Excel

3. В первом столбце (например, А) вводим информацию о величинах тяги реактивных двигателей самолетов-истребителей по данным, приведенным в табл. 2.

Введите данные (тягу) для каждого двигателя самолета (рис. 6).

Примечание 1: строка с надписью н.д. (табл. 2) – нет данных, в дальнейших расчетах не участвует и не записывается в заполняемый столбец. Примечание 2: ячейка А1 в данном случае представляет заголовок столбца и в дальнейших действиях, производимых со столбцами, не участвует.

Рис. 6. Ввод данных по параметру тяги реактивных двигателей

752

Раздел VII. Методы управления инновационными проектами

4. Далее для расчета дисперсии и среднего квадратичного отклонения необходимо, согласно (2-3), найти среднее значение параметра тяги, для этого после формирования столбца (в нашем случае это ячейка А44 (рис. 7)) вписываем в выделенную левой кнопкой «мыши» ячейку знак «=». После чего нажимаем на значок fx и, в всплывшем окне Мастер функций шаг 1 из 2 (рис. 7), выбираем функцию СРЗНАЧ, и нажимаем ОК (рис. 7). После этого система выведет второе окно Аргументы функции (рис. 8), где необходимо указать диапазон для расчета среднего значения, в нашем случае, это весь столбец «х – тяга, кГ» А2:А43, после этого нажимаем ОК, затем программа автоматически выведет численное значение искомой функции СРЗНАЧ, в нашем случае в ячейку А44 (рис. 7).

Рис. 7. Нахождение среднего значения параметра тяги реактивных двигателей

753

Раздел VII. Методы управления инновационными проектами

Рис. 8. Окно задания аргументов функции нахождения среднего значения

5. Далее формируем числитель дроби по расчету дисперсии, согласно (2) (рис. 9), для этого в выделенную ячейку (в нашем случае В2) после знака «=» вписываем формулу, показанную на рис. 9. Значком «$» фиксируем величину среднего значения по параметру тяги и с помощью комбинации клавиш shift 6 возводим в квадрат, согласно (2) (рис. 9). После чего подводим курсор «мыши» в правый нижний угол ячейки (в нашем случае это ячейка В2) и после появления значка «+» протягиваем столбец до конца ряда столбца А (в нашем случае ячейки В43) (рис. 10).

Рис. 9. Формирования столбца с числителем дроби в формуле нахождения дисперсии (2)

754

Раздел VII. Методы управления инновационными проектами

6. Далее находим сумму послученного столбца с числителем дроби (2), для этого в ячейке после яформированного столбца (в нашем случае это ячейка В44) вписываем знак «=» и нажимаем на значок fx и, в всплывшем окне Мастер функций шаг 1 из 2 (рис. 10), выбираем функцию СУММ, и нажимаем ОК (рис. 10). После этого система выведет второе окно Аргументы функции, где необходимо указать диапазон для расчета суммы, в нашем случае, это весь столбец «числитель дроби σ^2» В2:В43, после этого нажимаем ОК, затем программа автоматически выведет численное значение суммы искомой функции СУММ, в нашем случае в ячейку В44 (рис. 10).

Рис. 10. Нахождение суммы значений столбца В

755

Раздел VII. Методы управления инновационными проектами

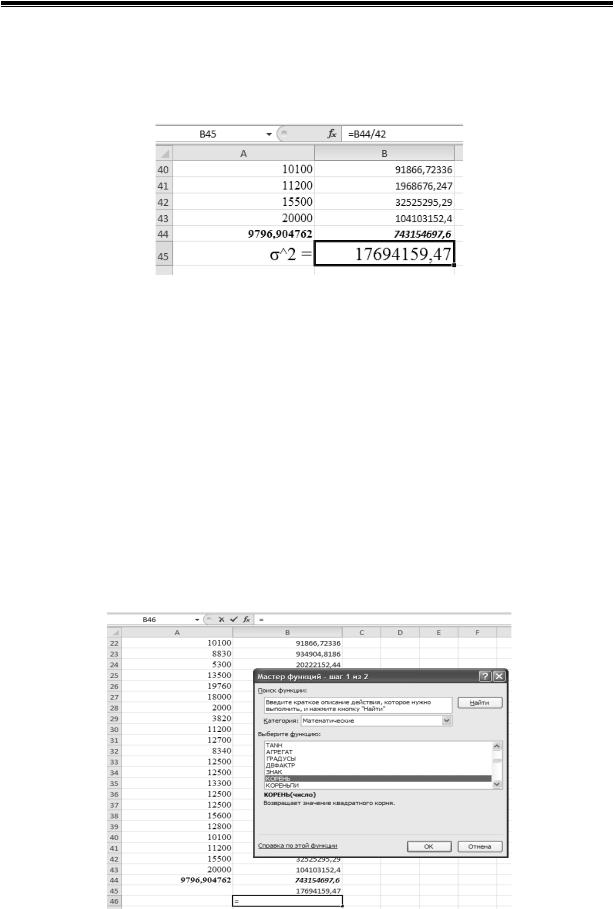
7. Далее (в нашем случае в ячейке В45 (рис. 11)) находим значение дисперсии согласно (2), напечатав знак «=» и разделив данные ячейки (в нашем случае В44 – сумма числителей дроби (2)) на 42 – общее число наблюдений (рис. 11).

Рис. 11. Расчет дисперсии по параметру тяги реактивных двигателей

8. Для расчета среднего квадратичного отклонения (3) необходимо найти квадратный корень от величины дисперсии (2). Для этого в ячейке ниже (в нашем случае это ячейка В46) печатаем знак «=» и нажимаем на значок fx и, в всплывшем окне Мастер функций шаг 1 из 2 (рис. 12), выбираем функцию КОРЕНЬ, и нажимаем ОК (рис. 12). После этого система выведет второе окно Аргументы функции (рис. 13), где необходимо указать число для расчета квадратного корня, в нашем случае, это ячейка В45 – величина дисперсии, после этого нажимаем ОК, затем программа автоматически выведет численное значение квадратного корня искомой функции КОРЕНЬ, в нашем случае в В46 (рис. 14).

Рис. 12. Нахождение квадратного корня для расчета среднего квадратичного отклонения (3)

756

Раздел VII. Методы управления инновационными проектами

Рис. 13. Задание аргументов функции КОРЕНЬ

Рис. 14. Расчет величины среднего квадратичного отклонения (3)

9. После нахождение величин дисперсии и среднего квадратичного отклонения по параметру тяги реактивных двигателей самолетов истребителей-перехватчиков необходимо сохранить файл формата *xls. Для этого нажать вкладку меню Файл → Сохранить как, либо нажать на крестик в правой верхнем углу и сохранить изменения в файле, дав ему название и выбрав место его расположения.

757

Раздел VII. Методы управления инновационными проектами

10. Для выполнения третьего задания лабораторной работы необходимо рассчитать величину дисперсии (2) и среднего квадратичного отклонения (3), коэффициент вариации (4), определить меру риска и математическое ожидание (5) по параметру тяги газотурбинных двигателей самолетов-истребителей (табл. 2) в системе MATLAB. Для этого можно либо запустить систему MATLAB заново, либо продолжать запись в файле, созданном при выполнении п. 1.

Примечание: Для очистки командного окна MATLAB необходимо выбрать вкладку меню Edit → Clear Command Window.

Создадим массив значений по параметру тяги, назовем его link, и массив дат первых полетов, назовём его time, для этого введем в командное окно системы MATLAB следующие 2 строки

(рис. 15):

link = [5200 5200 3250 5100 5200 9600 6400 7100 9600 9500 9210 8440 3800 9210 9210 10100 5740 10150 10210 7200 10100 8830 5300 13500 19760 18000 2000 3820 11200 12700 8340 12500 12500 13300 12500 12500 15600 12800 10100 11200 15500 20000];

time = [1951 1951 1954 1955 1955 1955 1956 1956 1956 1956 1957 1956 1957 1957 1958 1958 1959 1960 1961 1962 1962 1966 1964 1970 1987 2006 1952 1956 1966 1967 1977 1981 1987 1987 1988 1990 1997 1999 1961 1964 1975 2000];

и нажимаем клавишу Enter на клавиатуре.

Рис. 15. Ввод входных данных в виде массивов величин тяги и дат первых полетов самолетов-истрбителей с этими двигателями

Для наглядности покажем соотношение параметров тяги к датам полётов самолётов с этими двигателями, согласно табл. 2, для этого введем далее в командное окно системы MATLAB (рис. 16) строку:

fact_table = [time;link].

758

Раздел VII. Методы управления инновационными проектами

После чего программа автоматически построит матрицу соотношений тяги новых двигателей и дат первых полетов самолетов с этими двигателями:

fact_table =

Columns 41 through 42 1975 2000 15500 20000

11. Далее определим среднее квадратичное отклонение по параметру тяги по формуле (3), для этого в системе MATLAB предназначена команда std. Введем следующую строку в командное ок-

но (рис. 16):

Sx = round(std(link, 1)),

после чего нажимаем клавишу Enter на клавиатуре.

Система автоматически выведет значение среднего квадратичное отклонение: Sx = 4206 (рис. 16).

Далее определим дисперсию по формуле (2), для этого возведем в квадрат среднее квадратичное отклонение (3), в системе MATLAB это запишется следующим образом (рис. 17):

Dx = Sx.^2

после чего нажимаем клавишу Enter на клавиатуре.

Система автоматически выведет значение дисперсии: Dx = 17690436 (рис. 17).

759

Раздел VII. Методы управления инновационными проектами

Рис. 16. Работа в командном окне MATLAB

12. Далее для оценки риска определим математическое ожидание Mo по параметру тяги и коэффициент вариации V (рис. 17). В системе MATLAB это имеет следующий синтаксис:

Mo = round(mean(link))

и нажимаем клавишу Enter, после чего программа автоматически выведет значение искомой величины математического ожидания.

Далее для расчета коэффициента вариации запишем в командное окно системы строку (рис. 17):

V = Sx*100/ Mo

и нажимаем клавишу Enter, после чего программа автоматически выведет значение искомой величины коэффициента вариации.

760