2. Показатели динамики социально-экономических явлений.

Для количественной оценки динамики социально-экономических явлений применяются: абсолютные приросты, темпы роста и прироста, темпы наращивания и др.

Для расчета показателей рядов динамики на постоянной базекаждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называютсябазисными.

Для расчета показателей динамики на переменной базекаждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называютсяцепными.

• Абсолютный прирост- определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.

Базисный абсолютный прирост Δу_б исчисляется как разность между сравниваемым уровнем у_iи уровнем, принятым за постоянную базу сравненияy_o:

Δу_бi =y_i– у_о

Цепной абсолютный прирост Δу_ц – разность между сравниваемым уровнем у_i и уровнем, который ему предшествует,у_i-1:

Δу_цi=y_i–y_i-1

Между базисными и цепными абсолютными приростами существует связь: сумма базисных абсолютных приростов ∑ Δу_цi равна базисному абсолютному приросту последнего периода ряда динамики.

• Темп роста -характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах:

Базисные темпы ростаТр_бисчисляются делением сравниваемого уровняу_iна уровень, принятый за постоянную базу сравнения,: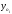

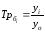
Цепные темпы ростаТр_цисчисляются делением сравниваемого уровняу_i на предыдущий уровеньу_i-1:

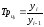
Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

Темп приростахарактеризует абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.

Базисный темп приростаТп_бвычисляется делением сравниваемого базисного абсолютного прироста Δу_бiна уровень, принятый за постоянную базу сравненияу_oi:

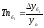
Цепной темп приростаТп_ц– это отношение сравниваемого цепного абсолютного прироста Δу_цi к предыдущему уровнюу_i-1:

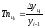
Между показателями темпа роста и прироста имеется взаимосвязь:

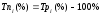(при выражении темпа роста в процентах).

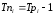(при выражении темпа роста в коэффициентах).

3. Средние показатели в рядах динамики

Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста и др.

Средний уровень рядадинамики характеризует типическую величину абсолютных уровней.

В интервальных рядах динамики средний уровень 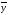определяется делением суммы уровней на их числоn:

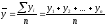
В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле средней хронологической:

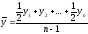
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле:

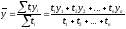, где

у_i– уровни ряда динамики, сохранившиеся без изменения в течение промежутка времениt_i.

Средний абсолютный приростпредставляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста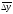сумма цепных абсолютных приростов ∑Δу_цiделится на их число: (гдеn– число уровней ряда)

.

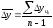Основываясь на взаимосвязи цепных и базисных абсолютных приростов, средний абсолютный прирост можно определить и по абсолютным уровням ряда динамики:

.

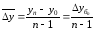Средний темп роста– обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа ростаТрприменяется формула средней геометрической:

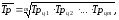
где Тр_ц1, Тр_ц2, …, Тр_цn-1– индивидуальные (цепные) темпы роста (в коэффициентах),

m– число индивидуальных темпов роста (m=n-1, гдеn- число уровней ряда).

Основываясь на взаимосвязи между цепных и базисных темпов роста средний темп роста можно определить по формуле и по абсолютным уровням ряда динамики

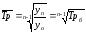
где n– число уровней ряда

• Средний темп прироста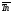можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста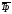для получения средних темпах прироста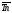используется зависимость:

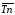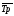= -1 (при выражении темпа роста в коэффициентах)