
- •5 Какое силовое поле называют потенциальным? Докажите, что однородное и центральное силовые поля являются потенциальными. Как определяется сила через потенциальную энергию?
- •24 Какие силы называют консервативными? Дайте определение потенциальной энергии. Как связаны между собой потенциальная энергия и сила поля.
- •29 Что такое волна? Уравнение бегущей плоской гармонической волны.
- •Плоские гармонические волны
- •46 Энтропия. Определение энтропии через термодинамическую вероятность. Приведите различные формулировки второго закона термодинамики.
5 Какое силовое поле называют потенциальным? Докажите, что однородное и центральное силовые поля являются потенциальными. Как определяется сила через потенциальную энергию?
Если работа сил поля, действующих на перемещающуюся в нём пробную частицу, не зависит от траектории частицы, и определяется только её начальным и конечным положениями, то такое поле называется потенциальным. Для него можно ввести понятие потенциальной энергии частицы — некоторой функции координат частиц такой, что разность её значений в точках 1 и 2 равна работе, совершаемой полем при перемещении частицы из точки 1 в точку 2.
Сила называется потенциальной, если существует скалярная функция, известная как потенциальная энергия и обозначаемая Ep, такая что
![]()
Если все силы, действующие на частицу консервативны, и Ep является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда: .
![]()
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
![]()
является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.
\
11 Запишите преобразования Лоренца для координат и времени. Выведите из них закон сложения скоростей в релятивистской механике.
x= y=y’ z=z’
t=
y=y’ z=z’
t=
Обратное преобразование Лоренца
x’=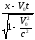 y’=y z’=z
t’=
y’=y z’=z
t’=
Пусть в системе отсчета K’
материальная точка движется вдоль оси
х’ спостоянной скоростью ![]() Система
K’ движется относительно системы K в
том же направлении со скоростью v ,
Определим, чему равна скорость материальной
точки vo,
относительно системы K, т.е. чему равно
Система
K’ движется относительно системы K в
том же направлении со скоростью v ,
Определим, чему равна скорость материальной
точки vo,
относительно системы K, т.е. чему равно ![]() .
Пусть при
.
Пусть при ![]() м.т.
находится в начале координат, причем
м.т.
находится в начале координат, причем ![]() .
Для системы K:
.
Для системы K:
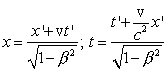
Подставляя ![]() и
t в формулу для vo
и
t в формулу для vo

Делим числитель и знаменатель на t

Это равенство выражает
собой релятивистский закон сложения
скоростей. При малых значениях
скоростей ![]() и
и ![]() имеем
имеем
![]()
т.е. релятивистский закон сложения скоростей переходит в классический.
18. Пружинный маятник. Выведите дифференциальное уравнение его свободных незатухающих колебаний и запишите его решение
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
|
Тогда
согласно второму закону Ньютона,
учитывая знаки проекций, получим:
тогда:
Или |
|
|
Выразим
ускорение:
|
|
|
Сравним полученное
уравнение с уравнением колебательного
движения
Видно,
что |
|
|
Период
колебаний
|
|
|
Аналогичные
вычисления можно проделать с помощью
закона сохранения энергии. Учтем, что
потенциальная энергия упруго
деформированного тела равна |
|
|
Запишем закон
сохранения энергии и возьмем производную
от левой и правой частей уравнения:
Т.к. производная
от постоянной величины равна нулю,
то
Производная
суммы равна сумме производных:
и
Следовательно: |
|
Свободные
затухающие колебания пружинного
маятника.
Для пружинного маятника массой m, который
совершает малые колебания под действием
упругой силы F= -kx, сила трения прямо
пропорциональна скорости, т. е.
![]() где
r — коэффициент
сопротивления;
знак минус говорит о том, что сила трения
и скорость противоположно направлены.
При
этих условиях закон движения
маятника
где
r — коэффициент
сопротивления;
знак минус говорит о том, что сила трения
и скорость противоположно направлены.
При
этих условиях закон движения
маятника
![]() (9)
Используя
формулу
(9)
Используя
формулу ![]() и
считая, что коэффициент затухания
равен
и
считая, что коэффициент затухания
равен
![]() (10)
получим
полностью идентичное уравнению (1)
дифференциальное уравнение затухающих
колебаний маятника:
(10)
получим
полностью идентичное уравнению (1)
дифференциальное уравнение затухающих
колебаний маятника:
![]() Из
выражений (1) и (5) следует, что колебания
маятника удовлетворяют уравнению
Из
выражений (1) и (5) следует, что колебания
маятника удовлетворяют уравнению
![]() где
частота
где
частота ![]() (см.
(4)).
Добротность
пружинного маятника, используя (8) и
(10),
(см.
(4)).
Добротность
пружинного маятника, используя (8) и
(10), ![]() .
.
23 Выведите уравнение колебательного движения, являющегося суперпозицией гармонических колебаний одного направления с близкими частотами. Изобразите результирующее колебание на графике. Как называется такой вид колебания?
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты
![]()
воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы этих колебаний (рис. 203). Tax как векторы A1 и А2 вращаются с одинаковой угловой скоростью 0, то разность фаз (2—1) между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет
![]() (144.1)
(144.1)
В выражении (144.1) амплитуда А и начальная фаза соответственно задаются соотношениями
![]() (144.2)
(144.2)
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (2—1) складываемых колебаний.
Проанализируем выражение (144.2) в зависимости от разности фаз (2—1):
1) 2—1 = ±2m (т=0, 1, 2, ...), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
2) 2—1 = ±(2m+1) (т=0, 1, 2, ...), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны и +, причем <<. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
![]()
Складывая эти выражения и учитывая, что во втором сомножителе /2<<, найдем
![]() (144.3)
(144.3)
Результирующее колебание (144.3) можно рассматривать как гармоническое с частотой , амплитуда Аб, которого изменяется по следующему периодическому закону:
![]() (144.4)
(144.4)
Частота изменения Аб в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:
![]()
Период биений
![]()
Характер зависимости (144.3) показан на рис. 204, где сплошные жирные линии дают график результирующего колебания (144.3), а огибающие их — график медленно меняющейся по уравнению (144.4) амплитуды.
Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями — наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.
Любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте 0:
![]() (144.5)
(144.5)
Представление периодической функции в виде (144.5) связывают с понятием гармонического анализа сложного периодического колебания, илиразложения Фурье.* Слагаемые ряда Фурье, определяющие гармонические колебания с частотами 0, 20, 30, ..., называются первой (или основной),второй, третьей и т. д. гармониками сложного периодического колебания.
* Ж. Фурье (1768—1830) — французский ученый.


 или
или