|
Уравнения
вида
 .В
этом случае примем .В
этом случае примем
 за независимую переменную и введем
новую функцию
за независимую переменную и введем
новую функцию
 .
Считая, что .
Считая, что
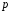 есть функция от
есть функция от
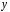 и через посредство
и через посредство
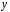 зависит от
зависит от
 и, применяя правило дифференцирования
сложных функций, получим для производных
от
и, применяя правило дифференцирования
сложных функций, получим для производных
от
 по
по
 выражения
выражения
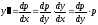 , , , ,
аналогично
вычисляются
 . .
Подставляя
в уравнение вместо
 и т.д., увидим, что в новых переменных
порядок уравнения будет
и т.д., увидим, что в новых переменных
порядок уравнения будет
 ,
т.е. на единицу ниже. Если это
преобразованное уравнение проинтегрировано
и ,
т.е. на единицу ниже. Если это
преобразованное уравнение проинтегрировано
и
 - его решение, то нахождение общего
интеграла данного уравнения сводится
к интегрированию
- его решение, то нахождение общего
интеграла данного уравнения сводится
к интегрированию   .Откуда
получаем общее решение ОДУ .Откуда
получаем общее решение ОДУ
 . .
|
|
линейного
дифференциального уравнения порядка
 с постоянными коэффициентами есть
с постоянными коэффициентами есть
|
 Общее решение
имеет вид
Общее решение
имеет вид
 ,где ,где являются корнями характеристического
уравнения
являются корнями характеристического
уравнения .Каждому
действительному корню .Каждому
действительному корню
 уравнения кратности
уравнения кратности
 соответствуют
соответствуют
 линейно независимых решений уравнения
линейно независимых решений уравнения
 , ,
а
каждой паре комплексных корней
 кратности
кратности
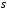 соответствуют
соответствуют
 пар линейно независимых решений:
пар линейно независимых решений:

 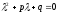 Если квадратное
уравнение имеет два различных
действительных корня
Если квадратное
уравнение имеет два различных
действительных корня
 и
и
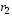 ,
то согласно имеем два линейно
независимых решения уравнения ,
то согласно имеем два линейно
независимых решения уравнения
 .Общее
решение имеет вид .Общее
решение имеет вид
 ,
Если квадратное уравнение имеет
комплексные корни ,
Если квадратное уравнение имеет
комплексные корни
 ,
тогда ,
тогда
общее решение
имеет вид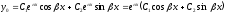 .
Если квадратное уравнение (2.22) имеет
два равных действительных корня .
Если квадратное уравнение (2.22) имеет
два равных действительных корня
 ,
то общее решение уравнения имеет вид ,
то общее решение уравнения имеет вид
 . .
|
|
Линейные
неоднородные дифференциальные
уравнения со специальной правой частью
|
 ,
где ,
где
 - многочлен
- многочлен
 -й
степени, -й
степени,
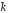 - число, или
- число, или
 ,
где ,
где
 - многочлены степени
- многочлены степени
 и
и
 ,
соответственно, ,
соответственно,
 - числа, частное решение
- числа, частное решение
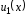 уравнения можно найти методом
неопределенных коэффициентов.А именно,
пусть правая часть имеет вид
уравнения можно найти методом
неопределенных коэффициентов.А именно,
пусть правая часть имеет вид
 .
1)Если .
1)Если
 не совпадает
ни с одним корнем характеристического
уравнения, то частное решение
не совпадает
ни с одним корнем характеристического
уравнения, то частное решение
 ищется в виде
ищется в виде
 ,где ,где
 - многочлен той же степени, что и
- многочлен той же степени, что и
 ,
но с
неопределенными коэффициентами,
которые надо найти. Для чего, вычисляя
с помощью ,
но с
неопределенными коэффициентами,
которые надо найти. Для чего, вычисляя
с помощью
 и подставляя в исходное уравнение ,
сокращаем правую и левую части на
и подставляя в исходное уравнение ,
сокращаем правую и левую части на
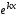 .
Приравнивая коэффициенты при одинаковых
степенях .
Приравнивая коэффициенты при одинаковых
степенях
 ,
получим систему уравнений для отыскания
неопределенных коэффициентов. Подставив
их , будем иметь искомое частное решение ,
получим систему уравнений для отыскания
неопределенных коэффициентов. Подставив
их , будем иметь искомое частное решение
 .2)Если .2)Если
 совпадает
с некоторым корнем характеристического
уравнения кратности
совпадает
с некоторым корнем характеристического
уравнения кратности
 ,
то частное решение ищется в виде ,
то частное решение ищется в виде
 . Дальнейшие
действия аналогичны предыдущему
случаю. Пусть теперь правая часть
уравнения имеет вид . Дальнейшие
действия аналогичны предыдущему
случаю. Пусть теперь правая часть
уравнения имеет вид
 .3)Если
число .3)Если
число
 не совпадает
ни с одним
из корней характеристического
уравнения, то частное решение ищется
в виде
не совпадает
ни с одним
из корней характеристического
уравнения, то частное решение ищется
в виде
 ,где ,где
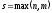 , ,
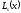 и
и
 многочлены одной
и той же степени
многочлены одной
и той же степени
 ,
но с разными
неопределенными коэффициентами,
которые находятся так же как и в первом
случае. 4) Если ,
но с разными
неопределенными коэффициентами,
которые находятся так же как и в первом
случае. 4) Если
 совпадает с некоторым корнем
характеристического уравнения
кратности
совпадает с некоторым корнем
характеристического уравнения
кратности
 ,
то выражение для частного решения
домножается на ,
то выражение для частного решения
домножается на
 ,
а именно ,
а именно ,
где ,
где
 , ,
 , ,
 те же, что и выше.
те же, что и выше.
Замечание
2. Многочлены с неопределенными
коэффициентами четвертой, третьей,
второй, первой, нулевой степени имеют
вид:
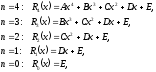
где
 неопределенные коэффициенты; многочлены
неопределенные коэффициенты; многочлены
 и
и

 выписываются аналогично
выписываются аналогично
 . .
|







 ,
, ,
,

 1)Метод
Лагранжа( метод вариации произвольной
постоянной
1)Метод
Лагранжа( метод вариации произвольной
постоянной 2)Метод
Бернулли
2)Метод
Бернулли
 Решим
уравнение
Решим
уравнение
 подставляя находим решение
подставляя находим решение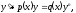 Делением
обеих частей на
Делением
обеих частей на
 и подстановкой
и подстановкой
 ,
где
,
где
 новая неизвестная функция, это уравнение
приводится к линейному уравнению
новая неизвестная функция, это уравнение
приводится к линейному уравнению
 .
.

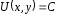 ;
;
 из
равенства
из
равенства находим
находим
 и
подставляем в решение
и
подставляем в решение .Общее
решение получается с помощью
.Общее
решение получается с помощью
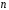 - кратного интегрирования
- кратного интегрирования ,где
,где

 .С
помощью замены
.С
помощью замены
 понизим порядок уравнения на
понизим порядок уравнения на
 единиц:
единиц:
 .Предположим,
что для полученного уравнения общее
решение имеет вид
.Предположим,
что для полученного уравнения общее
решение имеет вид
 .Тогда
искомая функция
.Тогда
искомая функция
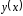 получается с помощью
получается с помощью
 кратного
интегрирования функции
кратного
интегрирования функции

 .В
этом случае примем
.В
этом случае примем
 за независимую переменную и введем
новую функцию
за независимую переменную и введем
новую функцию
 .
Считая, что
.
Считая, что
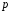 есть функция от
есть функция от
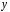 и через посредство
и через посредство
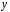 зависит от
зависит от
 и, применяя правило дифференцирования
сложных функций, получим для производных
от
и, применяя правило дифференцирования
сложных функций, получим для производных
от
 по
по
 выражения
выражения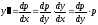 ,
, ,
, .
. и т.д., увидим, что в новых переменных
порядок уравнения будет
и т.д., увидим, что в новых переменных
порядок уравнения будет
 ,
т.е. на единицу ниже. Если это
преобразованное уравнение проинтегрировано
и
,
т.е. на единицу ниже. Если это
преобразованное уравнение проинтегрировано
и
 - его решение, то нахождение общего
интеграла данного уравнения сводится
к интегрированию
- его решение, то нахождение общего
интеграла данного уравнения сводится
к интегрированию

 .Откуда
получаем общее решение ОДУ
.Откуда
получаем общее решение ОДУ
 .
. Общее решение
имеет вид
Общее решение
имеет вид
 Если известно общее решение
Если известно общее решение
 соответствующего уравнению однородного
уравнения , то для определения частного
решения
соответствующего уравнению однородного
уравнения , то для определения частного
решения

 уравнения можно воспользоваться
методом Лагранжа вариации произвольных
постоянных. Решение
уравнения может быть получено по
формуле:
уравнения можно воспользоваться
методом Лагранжа вариации произвольных
постоянных. Решение
уравнения может быть получено по
формуле:

 с постоянными коэффициентами есть
с постоянными коэффициентами есть
 Общее решение
имеет вид
Общее решение
имеет вид
 ,где
,где являются корнями характеристического
уравнения
являются корнями характеристического
уравнения .Каждому
действительному корню
.Каждому
действительному корню
 уравнения кратности
уравнения кратности
 соответствуют
соответствуют
 линейно независимых решений уравнения
линейно независимых решений уравнения
 ,
,
 кратности
кратности
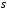 соответствуют
соответствуют
 пар линейно независимых решений:
пар линейно независимых решений:

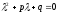 Если квадратное
уравнение имеет два различных
действительных корня
Если квадратное
уравнение имеет два различных
действительных корня
 и
и
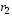 ,
то согласно имеем два линейно
независимых решения уравнения
,
то согласно имеем два линейно
независимых решения уравнения
 .Общее
решение имеет вид
.Общее
решение имеет вид
 ,
Если квадратное уравнение имеет
комплексные корни
,
Если квадратное уравнение имеет
комплексные корни
 ,
тогда
,
тогда
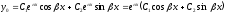 .
Если квадратное уравнение (2.22) имеет
два равных действительных корня
.
Если квадратное уравнение (2.22) имеет
два равных действительных корня
 ,
то общее решение уравнения имеет вид
,
то общее решение уравнения имеет вид
 .
.
 ,
где
,
где
 - многочлен
- многочлен
 -й
степени,
-й
степени,
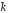 - число, или
- число, или
 ,
где
,
где
 - многочлены степени
- многочлены степени
 и
и
 ,
соответственно,
,
соответственно,
 - числа, частное решение
- числа, частное решение
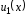 уравнения можно найти методом
неопределенных коэффициентов.А именно,
пусть правая часть имеет вид
уравнения можно найти методом
неопределенных коэффициентов.А именно,
пусть правая часть имеет вид
 .
1)Если
.
1)Если
 не совпадает
ни с одним корнем характеристического
уравнения, то частное решение
не совпадает
ни с одним корнем характеристического
уравнения, то частное решение
 ищется в виде
ищется в виде ,где
,где
 - многочлен той же степени, что и
- многочлен той же степени, что и
 ,
но с
неопределенными коэффициентами,
которые надо найти. Для чего, вычисляя
с помощью
,
но с
неопределенными коэффициентами,
которые надо найти. Для чего, вычисляя
с помощью
 и подставляя в исходное уравнение ,
сокращаем правую и левую части на
и подставляя в исходное уравнение ,
сокращаем правую и левую части на
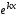 .
Приравнивая коэффициенты при одинаковых
степенях
.
Приравнивая коэффициенты при одинаковых
степенях
 ,
получим систему уравнений для отыскания
неопределенных коэффициентов. Подставив
их , будем иметь искомое частное решение
,
получим систему уравнений для отыскания
неопределенных коэффициентов. Подставив
их , будем иметь искомое частное решение
 .2)Если
.2)Если
 совпадает
с некоторым корнем характеристического
уравнения кратности
совпадает
с некоторым корнем характеристического
уравнения кратности
 ,
то частное решение ищется в виде
,
то частное решение ищется в виде
 . Дальнейшие
действия аналогичны предыдущему
случаю. Пусть теперь правая часть
уравнения имеет вид
. Дальнейшие
действия аналогичны предыдущему
случаю. Пусть теперь правая часть
уравнения имеет вид
 .3)Если
число
.3)Если
число
 не совпадает
ни с одним
из корней характеристического
уравнения, то частное решение ищется
в виде
не совпадает
ни с одним
из корней характеристического
уравнения, то частное решение ищется
в виде
 ,где
,где
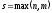 ,
,
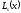 и
и
 многочлены одной
и той же степени
многочлены одной
и той же степени
 ,
но с разными
неопределенными коэффициентами,
которые находятся так же как и в первом
случае. 4) Если
,
но с разными
неопределенными коэффициентами,
которые находятся так же как и в первом
случае. 4) Если
 совпадает с некоторым корнем
характеристического уравнения
кратности
совпадает с некоторым корнем
характеристического уравнения
кратности
 ,
то выражение для частного решения
домножается на
,
то выражение для частного решения
домножается на
 ,
а именно
,
а именно ,
где
,
где
 ,
,
 ,
,
 те же, что и выше.
те же, что и выше.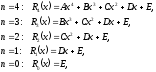
 неопределенные коэффициенты; многочлены
неопределенные коэффициенты; многочлены
 и
и

 выписываются аналогично
выписываются аналогично
 .
.